新算法思想孵化器：CEC05 benchmark的创新潜能


参考资源链接：[CEC2005真实参数优化测试函数与评估标准](https://wenku.csdn.net/doc/ewbym81paf?spm=1055.2635.3001.10343)
# 1. CEC05基准测试简介

## 算法基准测试的必要性
在IT领域，特别是算法研究和开发中，基准测试作为一种评估方法，至关重要。它能够为算法的性能提供一个公平且可量化的比较平台。CEC05基准测试是针对优化算法设计的一套标准测试集，旨在通过一系列具有挑战性的优化问题，来测试和验证算法的效率和可靠性。

## CEC05基准测试的特点
CEC05基准测试集涵盖了多种类型的问题，如单目标优化、多目标优化、大规模问题等。它通过设计复杂多变的测试案例，对算法在不同条件下的性能进行全面考量。这不仅有助于算法开发者找出潜在的弱点，也便于最终用户根据测试结果选择最合适的算法解决方案。

## 基准测试与实际应用
虽然基准测试提供了算法性能的参考，但将测试结果直接应用于实际问题时，需要考虑实际问题的特定约束和环境因素。本章将介绍CEC05基准测试的背景、目的以及如何为算法性能提供客观的评价标准，为后续深入了解CEC05算法的理论和实践打下基础。

# 2. CEC05算法的理论基础

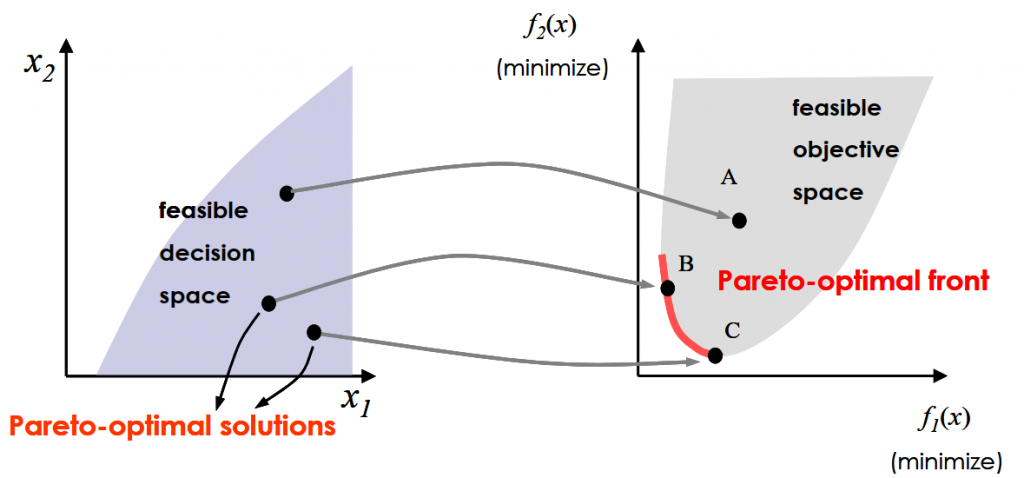
### 2.1 优化问题的数学模型

优化问题在数学、工程、经济等多个领域广泛存在。在这些领域中，找到最优解或满意解是实现资源最优化利用和性能最大化提升的关键。

#### 2.1.1 问题定义与目标函数

目标函数是优化问题的核心，它定义了需要最大化或最小化的性能指标。在CEC05算法中，目标函数通常是高维、非线性、多峰的复杂函数。

\min f(\mathbf{x}) \quad \text{where} \quad \mathbf{x} = (x_1, x_2, ..., x_n) \in \mathbb{R}^n

上述公式表示，在一个n维空间内，我们寻找使得目标函数f(x)达到最小值的解向量x。

#### 2.1.2 约束条件的表达方式

在实际应用中，优化问题往往伴随一定的约束条件，这些条件定义了解空间的可行区域。根据CEC05测试集的特点，约束条件通常包含等式和不等式约束。

g_i(\mathbf{x}) \leq 0, \quad i = 1, 2, ..., m
h_j(\mathbf{x}) = 0, \quad j = 1, 2, ..., p

这些公式定义了m个不等式约束和p个等式约束，只有满足所有约束条件的解才是可行解。

### 2.2 CEC05算法的进化机制

CEC05算法是基于群体智能的优化算法，它模拟自然界中的进化过程。该算法通过选择、变异和交叉等操作不断地进化个体，以期在解空间中寻找到最优解。

#### 2.2.1 进化策略与选择过程

进化策略主要是指算法如何在每一代中选择出下一代的个体。CEC05算法通常使用轮盘赌选择、锦标赛选择等策略来保留优秀个体。

# 轮盘赌选择算法示例代码
def roulette_wheel_selection(fitness, total_fitness):
    random_value = random.uniform(0, total_fitness)
    current = 0
    for i, fit in enumerate(fitness):
        current += fit
        if current > random_value:
            return i

在上述Python代码中，我们利用轮盘赌选择机制根据个体的适应度进行选择。每个个体被选中的概率与适应度值成正比。

#### 2.2.2 变异与交叉操作的原理

变异操作负责在解空间中引入新的遗传多样性，防止算法早熟收敛。CEC05算法中的变异操作可以是高斯变异、多项式变异等。

\mathbf{x}' = \mathbf{x} + \alpha \times \mathbf{N}(0,1)

其中，x是当前个体，α是步长控制因子，N(0,1)表示均值为0、方差为1的正态分布随机数。

交叉操作是产生新个体的另一种方式，它结合两个父代个体的信息，产生子代个体。CEC05算法中常采用单点交叉、均匀交叉等策略。

# 单点交叉算法示例代码
def single_point_crossover(parent1, parent2, crossover_point):
    size = len(parent1)
    assert size == len(parent2)
    child1 = parent1[:crossover_point] + parent2[crossover_point:]
    child2 = parent2[:crossover_point] + parent1[crossover_point:]
    return child1, child2

在这个Python代码示例中，我们实现了单点交叉操作，通过交叉点将两个父代个体的部分信息交换，从而产生子代。

### 2.3 算法参数对性能的影响

算法的性能往往受参数设定的影响。为了确保CEC05算法能够高效运行并寻找到全局最优解，需要对算法参数进行精细的调优。

#### 2.3.1 参数调优的理论基础

参数调优是一个系统化的过程，需要根据问题的特性进行。理论基础包括了参数对算法收敛速度和解的质量的影响分析。

#### 2.3.2 实验分析与参数选择指南

在实际操作中，我们通常借助实验数据来指导参数的选取。通过对比不同参数设定下的算法性能，可以找到较优的参数组合。

graph LR
    A[问题定义] --> B[参数设定]
    B --> C[实验设计]
    C --> D[算法执行]
    D --> E[性能评估]
    E --> F[参数调优]
    F --> G[优化策略选择]

以上mermaid流程图展示了参数调优的整体流程，包括问题定义、参数设定、实验设计、算法执行、性能评估、参数调优和最终的优化策略选择。

以上章节内容详细阐述了CEC05算法的理论基础，从问题定义到参数调优的系统化方法，为算法的实践操作打下了坚实的基础。下一章节将具体介绍算法实践操作的步骤与方法。

# 3. CEC05算法实践操作

## 3.1 算法实现的软件框架

### 3.1.1 开发环境和工具选择

在开始CEC05算法的实现之前，选择合适的开发环境和工具至关重要，因为它们直接影响算法的开发效率和最终性能。对于CEC05算法的实践操作，推荐使用以下几个开发工具和环境：

- **编程语言**：在进行CEC05算法的实践操作中，编程语言的选择至关重要。大多数情况下，选择C++、Python或者Java是最为常见的，因为这些语言有着丰富的库和框架支持算法的开发与优化。
- **集成开发环境（IDE）**：推荐使用如Visual Studio Code、PyCharm或Eclipse等IDE，它们提供了代码编写、调试、版本控制等功能，大幅提高开发效率。
- **科学计算库**：对于算法开发，尤其是涉及到数学模型和统计分析的场景，如NumPy、SciPy（Python）、Armadillo（C++）等科学计算库将非常有帮助。

### 3.1.2 关键代码段的实现细节

接下来，我们探讨CEC05算法中关键代码段的实现细节。以问题定义与目标函数的初始化为例，下面是一个简单的代码段，展示了如何使用Python语言进行初始化：

import numpy as np

# 目标函数定义
def objective_function(x):
    return np.sum(x**2)

# 初始化参数
n_dimensions = 10  # 问题的维度
lower_bounds = np.full(n_dimensions, -10)  # 参数下界
upper_bounds = np.full(n_dimensions, 10)   # 参数上界

# 随机生成初始种群
population = np.random.uniform(lower_bounds, upper_bounds, (n_dimensions, 10))

# 计算初始种群的适应度