混合加权定位技术：复杂环境下的性能评估与实战技巧


参考资源链接：[MATLAB实现Chan-Taylor混合加权算法进行TDOA定位](https://wenku.csdn.net/doc/aibjxu0sw0?spm=1055.2635.3001.10343)
# 1. 混合加权定位技术概述

在现代信息技术的推动下，定位技术已经深入到生活的方方面面，从物流跟踪到无人驾驶，再到紧急救援等领域。混合加权定位技术，作为一项先进的定位方法，通过综合不同定位手段的定位数据，优化了定位的精度和可靠性。该技术融合了多种传感器数据，并运用加权算法对这些数据进行处理，以期达到在复杂环境中也能提供稳定准确位置信息的目标。混合加权定位技术的广泛应用前景和其在提高定位精度方面的显著优势，使其成为IT领域研究和发展的热点话题。

# 2. 理论基础与数学模型

## 2.1 定位技术的基本理论
定位技术的发展历程是理解现代混合加权定位技术不可或缺的部分。本节将从历史角度出发，简述定位技术的发展脉络，并详细探讨影响定位性能的关键指标。

### 2.1.1 定位技术的历史与发展
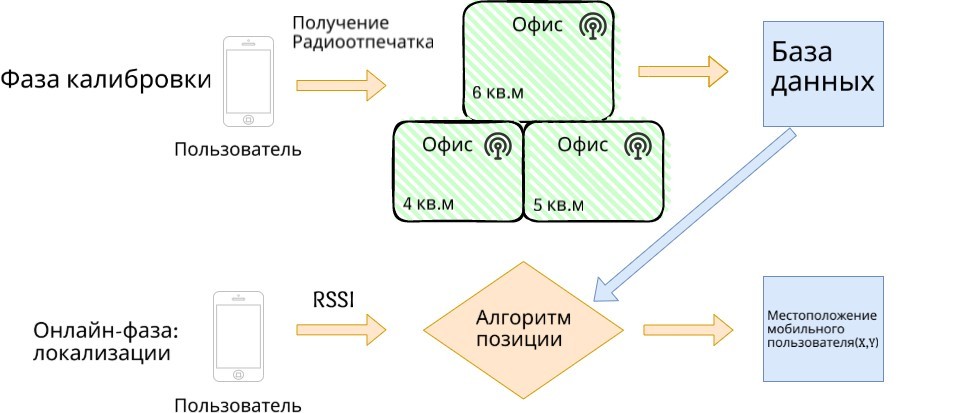
从最早的基于方位和距离的定位方法到现代的卫星导航系统，定位技术经历了多次革新。早期的定位方法包括无线电测向（Radio Direction Finding, RDF）、时间差定位（Time Difference of Arrival, TDOA）等。随着技术的发展，卫星导航系统如全球定位系统（Global Positioning System, GPS）和全球导航卫星系统（Global Navigation Satellite System, GLONASS）为精确位置服务提供了新的可能性。进入21世纪，随着互联网和物联网（IoT）技术的兴起，混合加权定位技术应运而生，它结合了多种定位技术的优势，通过数学建模和数据融合，提高了定位精度和可靠性。

### 2.1.2 定位技术的关键性能指标
定位技术的关键性能指标包括但不限于定位精度、定位速度、定位可靠性和成本效率。定位精度是指定位结果的准确性，通常以米（m）或分米（dm）为单位衡量。定位速度指的是从开始定位到获得位置信息所需的时间。定位可靠性涉及到定位结果的一致性和在不同条件下的稳定性。成本效率则考量了定位系统的整体开销，包括硬件成本、运营成本和维护成本。这些指标直接决定了定位技术在实际应用中的表现和可行性。

## 2.2 混合加权定位模型
混合加权定位模型是将多种定位方法进行融合，通过数学建模实现对目标位置的估计。本节重点介绍该模型的理论框架和权重确定方法。

### 2.2.1 混合加权模型的理论框架
混合加权模型通过综合多个定位源的信息，利用各自的优势来提升定位的性能。具体而言，模型需要确定不同定位源对最终定位结果的贡献度，也即权重。权重的确定不是静态的，而是根据当前的信号质量和环境条件动态调整。该模型通常可以表示为一个加权和的形式，其中每个定位源的测量值都被赋予了一个权重，以反映其在特定情境下的有效性。

### 2.2.2 权重的确定与影响因素
权重的确定是混合加权模型中的核心问题之一。权重的确定方法通常考虑如下因素：

- 信号质量：包括信号的强度、信噪比和误差率等指标。
- 环境特性：环境因素如室内或室外、开阔或遮蔽，都可能影响信号的传播特性。
- 设备性能：不同定位设备的性能和测量精度各有差异。
- 先验知识：如环境布局、运动模式等先验信息，可以用来辅助权重的确定。

权重的确定方法通常包括经验公式、机器学习方法和模糊逻辑等。

## 2.3 数学模型的构建与优化
在本节中，我们将深入探讨数学模型构建和优化的策略，特别是定位误差模型的建立和优化方法。

### 2.3.1 定位误差模型的建立
建立一个准确的定位误差模型是提高定位系统性能的关键步骤。通常，误差模型会包括多个组成部分，如系统误差、随机误差和环境误差。系统误差是由定位设备的硬件和软件不完美性导致的，可以透过校准方法来减小。随机误差通常与信号噪声或测量方法有关，通过提高测量技术或信号处理方法可以减小其影响。环境误差主要受到环境变化的影响，例如多径效应和信号遮挡。这些误差因素通常需要通过实测数据进行建模，并在算法中进行补偿或消除。

### 2.3.2 模型优化策略
为了进一步优化定位模型，需要采取一些策略来减少误差模型的影响。策略之一是利用先进的信号处理技术，例如卡尔曼滤波器，来平滑位置估计结果。此外，机器学习技术可以用于从历史数据中学习误差模式，并用于未来的定位计算中进行补偿。最后，对于模型的优化，通过不断迭代和测试，持续调整模型参数是提高定位精度的有效方式。

在此过程中，我们通常会使用一些优化算法，比如粒子群优化（PSO）、遗传算法（GA）等。这些算法可以帮助我们在全局搜索空间中寻找最佳的模型参数，以达到优化的目的。

为了更直观地理解，我们可以构建一个简单的示例来展示混合加权定位模型的构建过程。

假设我们有三个定位器 A、B、C 分别提供一组测量数据，我们需要根据权重分配确定最终的定位点 P(x, y)。

import numpy as np
import matplotlib.pyplot as plt

# 假定测量坐标和真实坐标
A_coords = np.array([2, 3])
B_coords = np.array([5, 3])
C_coords = np.array([3, 7])
true_coords = np.array([4, 5])

# 计算两两之间的距离
d_A = np.sqrt((A_coords[0] - true_coords[0]) ** 2 + (A_coords[1] - true_coords[1]) ** 2)
d_B = np.sqrt((B_coords[0] - true_coords[0]) ** 2 + (B_coords[1] - true_coords[1]) ** 2)
d_C = np.sqrt((C_coords[0] - true_coords[0]) ** 2 + (C_coords[1] - true_coords[1]) ** 2)

# 权重分配（这里为简化示例，使用距离的倒数）
weight_A = 1 / d_A
w