【贝叶斯网络与Kronecker积】：概率推理的新视角


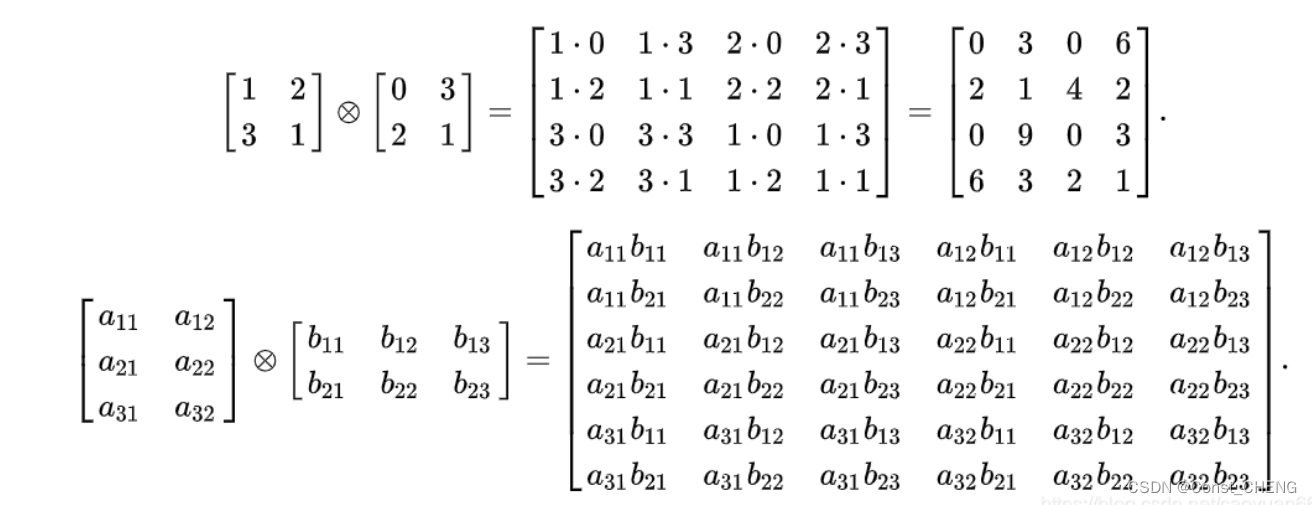
参考资源链接：[矩阵运算：Kronecker积的概念、性质与应用](https://wenku.csdn.net/doc/gja3cts6ed?spm=1055.2635.3001.10343)
# 1. 贝叶斯网络基础

在开始了解贝叶斯网络之前，理解其定义和结构是非常重要的一步。贝叶斯网络是一种概率图模型，它通过有向无环图（DAG）表示变量之间的依赖关系，并结合条件概率表（CPT）来描述变量的概率分布。这种模型特别适合表示和处理不确定性和概率推理问题。

## 条件独立性和贝叶斯网络的表示能力
贝叶斯网络的核心思想是条件独立性。它允许我们将复杂的联合概率分布分解成多个局部的、更为简单的分布，从而大幅简化计算。借助这种分解，贝叶斯网络能够高效地进行概率推断，比如预测和诊断。

## 贝叶斯网络的概率推理基础
概率推理是贝叶斯网络的灵魂，它涉及到在已知部分信息的情况下，如何计算其他未知变量的概率。推理过程依赖于网络结构和概率表，常见的推理方法包括变量消除法、信念传播算法和马尔可夫链蒙特卡洛（MCMC）方法等。

## 贝叶斯网络的学习和推断方法
贝叶斯网络的构建和应用需要通过学习和推断来不断优化。学习过程包括参数学习和结构学习，目标是找到最适合数据的网络模型。推断过程则是使用已经学习到的模型来计算新的数据的概率分布。两者是贝叶斯网络在实际应用中不断迭代和优化的重要步骤。

# 2. Kronecker积在概率推理中的应用

## 3.1 模型设计原则和方法论

### 3.1.1 概率图模型的选择与构建

在构建贝叶斯网络模型时，选择一个合适的概率图模型至关重要。概率图模型是一种表示变量间概率关系的图模型，其中贝叶斯网络是最常见的类型之一。构建一个模型需要考虑问题的领域知识、数据可用性和推理需求。以下是构建概率图模型时的一些指导原则：

1. **领域知识的重要性**：在构建模型之前，需要深入了解研究领域的基本概念和变量间的关系。领域专家的知识对于确定变量间的因果关系和概率分布至关重要。

2. **变量的定义**：确定哪些变量需要包含在模型中，这些变量可以是可观测的也可以是潜在的。对于每个变量，需要确定其可能的状态或取值范围。

3. **因果关系的表达**：使用有向边来表示变量间的因果关系。在贝叶斯网络中，每个节点代表一个随机变量，节点间的有向边代表变量间的依赖关系。

4. **概率分布的选择**：为每个变量分配合适的概率分布。这可能基于先验知识或从数据中学习得到。

5. **图形结构的简化**：尽可能简化模型的图形结构，去除不必要的复杂性和冗余依赖，以提高推理效率。

下面是一个简单的贝叶斯网络构建示例：

graph TD;
    A[环境因素] -->|依赖| B[健康状况]
    B -->|影响| C[医疗成本]

在这个示例中，环境因素直接影响健康状况，而健康状况又会影响医疗成本。这个简单的网络可以帮助分析和预测环境变化如何影响医疗支出。

### 3.1.2 确定变量、因子和条件概率分布

在构建贝叶斯网络模型时，确定变量的因子和条件概率分布是关键的一步。以下步骤可以帮助进行这一过程：

1. **变量的类型和范围**：首先要确定每个变量是离散的还是连续的，并定义它们的状态或取值范围。

2. **因子的确定**：对于每个变量，确定影响它的因素，即哪些其他变量会直接影响其概率分布。

3. **条件概率表（CPT）**：对于每个变量，基于其父变量的状态，确定条件概率表。CPT列出了每个变量在给定父变量状态下的概率分布。

4. **参数学习**：如果缺乏先验知识，可以通过数据学习参数。例如，可以使用最大似然估计（MLE）或贝叶斯估计方法来确定CPT中的概率值。

5. **结构的验证和更新**：在初步构建模型后，应进行验证和测试，确保模型结构和参数的合理性，并根据需要进行调整。

举个例子，如果一个变量“天气状况”有两个父变量“季节”和“地理环境”，则需要为“天气状况”创建一个三变量的条件概率表。假设每个父变量都有两个状态，那么将需要8个概率值来完全描述“天气状况”的CPT。

通过上述步骤，可以构建出一个精确且结构合理的贝叶斯网络模型，为进一步的概率推理和决策分析提供基础。

# 3. 理论与实践的结合：构建贝叶斯网络模型

## 3.1 模型设计原则和方法论
### 3.1.1 概率图模型的选择与构建

在实际问题求解中，选择合适概率图模型是成功的关键一步。概率图模型能够直观地表示变量之间的依赖关系，贝叶斯网络因其直观的网状结构和坚实的数学基础，成为应用最广泛的概率图模型之一。构建贝叶斯网络模型，本质上是要通过有向无环图（DAG）的结构来捕捉变量间的条件独立性。以下是构建贝叶斯网络模型的基本步骤和方法论：

1. **变量识别**：首先，需要明确要分析的问题，并识别出所有相关的随机变量。这些变量可以是可观测的，也可以是潜在的，它们将构成模型的节点。

2. **依赖关系分析**：对变量之间的依赖性进行分析，确定哪些变量是相互独立的，哪些是有条件依赖的。这一步至关重要，因为后续的推理将基于这些依赖关系进行。

3. **DAG结构确定**：确定好变量之间的依赖关系后，接下来就是构建一个有向无环图，每个节点代表一个随机变量，有向边表示变量间的依赖关系。如果两节点间不存在直接依赖，它们之间就不存在边。

4. **条件概率分配**：每一个节点都要分配条件概率表（CPT），这些概率值反映了给定父节点状态下该节点状态的概率。CPT的获取可以通过专家知识、统计数据或者机器学习方法来确定。

### 3.1.2 确定变量、因子和条件概率分布

在构建贝叶斯网络时，除了需要识别变量和它们之间的依赖关系外，还需明确变量的概率分布类型，这通常依赖于实际问题的性质和可用的数据。下面详细介绍如何确定变量类型和条件概率分布：

1. **变量类型**：根据变量的性质，变量可以分为离散变量和连续变量。离散变量的概率分布可用概率质量函数（PMF）表示，而连续变量的概率分布可用概率密度函数（PDF）表示。

2. **因子选择**：对于每个变量，我们需要确定其父节点（即该变量的直接前驱变量）以及父节点的状态。根据父节点的状态，变量将拥有一系列条件概率分布。

3. **条件概率表（CPT）的构建**：对于每个变量，条件概