空间回归分析从入门到精通：GeoDa实操案例解析


参考资源链接：[GeoDa使用手册（中文版）](https://wenku.csdn.net/doc/6412b654be7fbd1778d4655b?spm=1055.2635.3001.10343)
# 1. 空间回归分析基础

空间回归分析是利用空间数据来研究地理现象或空间结构关系的一类统计分析方法。在数据科学和地理信息系统（GIS）领域中，空间回归分析有着广泛的应用。它帮助研究者们理解和预测地理位置上的变量间的关系，以及空间分布模式。

## 1.1 空间数据的特征

空间数据包含了位置信息、空间关系以及空间分布特征。理解这些特征对于深入空间回归分析至关重要。与传统统计分析不同，空间回归分析必须考虑空间依赖性与空间异质性，即所谓的“空间效应”。

## 1.2 空间依赖性与空间异质性

- 空间依赖性：指在空间上的观测值之间存在相互影响或相互关联的特性。例如，邻近地区的房价可能会相互影响。
- 空间异质性：指的是不同地理位置上变量间关系的不均匀性。例如，不同城市之间经济发展水平与环境质量之间的关系可能截然不同。

在后续章节中，我们将深入探讨如何在GeoDa软件中处理这些空间数据特征，并进行空间回归模型的构建和分析。接下来的章节将介绍GeoDa的基本界面与操作，以及如何导入和管理空间数据，为进行空间回归分析打下坚实基础。

# 2. GeoDa软件界面与基本操作

## 2.1 GeoDa界面概览

### 2.1.1 工作区布局和功能组件

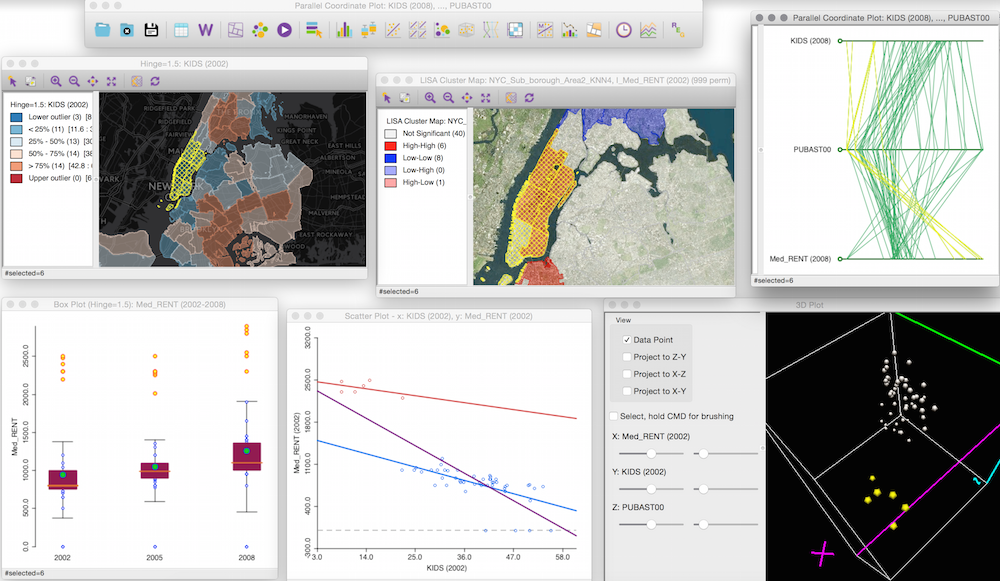
GeoDa是一款专门用于空间数据分析和可视化的软件，它以用户友好的界面著称，使得空间数据分析变得更加直观和易于操作。工作区是GeoDa软件中进行数据操作和分析的主要区域，用户与数据的每一次交互都在这个区域内进行。

GeoDa界面可以清晰地划分为以下几个主要部分：

- **菜单栏**: 提供各种操作和功能的入口，如文件操作、数据管理、空间分析工具等。
- **工具栏**: 为常用功能提供快捷操作，例如打开数据、保存项目、地图视图切换等。
- **地图窗口**: 显示空间数据的地图视图，是进行空间分析的核心区域。
- **图层控制面板**: 管理地图上显示的数据图层，可以控制图层的显示、隐藏、顺序等。
- **属性表**: 显示数据属性信息，支持数据的查询、选择、排序等操作。
- **侧边栏**: 包含各种空间分析工具，如散点图、统计量计算、空间自相关分析等。

GeoDa的设计初衷是让空间分析初学者快速上手，并让经验丰富的研究者能够高效地完成复杂的空间分析任务。

### 2.1.2 数据视图和地图展示方式

GeoDa支持多种数据视图和地图展示方式，以适应不同的分析需求：

- **栅格数据视图**: 常用于遥感图像和地形数据的展示。
- **矢量数据视图**: 用于展示点、线、多边形等几何类型的空间数据。
- **地图布局**: 提供布局视图，方便用户进行地图的排版和打印。
- **比例尺和指北针**: 在地图上添加比例尺和指北针，增加地图的表达清晰度。
- **图例和注释**: 管理图例信息和添加必要的注释，以帮助解释地图内容。

GeoDa支持的数据展示方式为用户提供了灵活的空间数据可视化手段，能够针对不同的数据和分析目的选择最合适的展示方式。

## 2.2 GeoDa的数据导入与管理

### 2.2.1 导入不同格式的空间数据

GeoDa支持导入多种格式的空间数据，包括常见的GIS格式如Shapefile、GeoJSON、KML等，同时也能导入CSV和Excel等表格数据格式，并将其转换为GIS图层。导入过程非常简单：

1. 点击菜单栏中的"文件" > "打开"，选择要导入的数据文件。
2. GeoDa会自动识别文件类型，并提示用户进行下一步操作，如指定地理坐标参考系统（CRS）。
3. 对于表格数据，用户需要指定用于地理定位的列，GeoDa将根据这些信息创建空间图层。

### 2.2.2 数据清洗和预处理技巧

在进行深入的空间分析之前，数据的清洗和预处理是必不可少的步骤。GeoDa提供了多种工具以帮助用户进行数据管理：

- **数据过滤**: 通过查询条件筛选特定的数据记录。
- **数据编辑**: 手动添加、修改或删除数据属性和几何特征。
- **数据合并**: 将多个数据集合并到一个图层中，便于分析。
- **数据转换**: 改变图层的坐标系统，进行坐标转换。

此外，GeoDa还提供了一些高级的预处理技巧，例如数据重采样和空间插值，这些功能可以帮助用户处理不完整或不准确的数据，为后续分析打下良好的基础。

## 2.3 GeoDa的空间数据分析工具

### 2.3.1 空间权重矩阵的构建与应用

空间权重矩阵是进行空间统计分析的基础。在GeoDa中构建空间权重矩阵需要以下步骤：

1. 选择空间分析工具栏中的"空间权重"选项。
2. 在弹出的界面中，定义空间邻近关系，如基于距离或邻接的权重设置。
3. 保存构建完成的空间权重矩阵，并在后续的空间分析中调用。

构建完空间权重矩阵后，可以应用于空间回归分析、空间自相关分析等高级空间统计模型中。

### 2.3.2 空间统计量的计算和解释

GeoDa为用户提供了丰富的时间序列分析工具，可以计算全局和局部的空间统计量：

- **全局Moran's I**: 评估全局空间自相关的统计指标。
- **局部Moran's I**: 识别局部空间自相关的热点或冷点区域。
- **Getis-Ord Gi* (Gi*)**: 分析局部区域的空间聚集程度。

在计算统计量后，GeoDa会以地图的形式直观展示结果，并允许用户根据需要进行进一步的分析和解释。这种直观的展示有助于用户快速理解数据的空间分布特征和内在的模式。

这些空间统计分析工具是探索和理解空间数据关键特征的重要手段，为研究者提供了强大的分析支持。

# 3. 探索性空间数据分析（ESDA）

## 3.1 空间自相关分析

### 3.1.1 全局空间自相关指标

空间自相关是指空间数据中相似或不相似属性值在空间位置上的聚集程度。全局空间自相关通常通过Moran's I和Geary's C两种指标来度量。Moran's I的值域在-1到1之间，接近1表示强正空间自相关，接近-1表示强负空间自相关，接近0表示空间随机分布。全局空间自相关指标能够反映整个研究区域的空间分布特征，是探索性空间数据分析的重要组成部分。

graph LR
A[全局空间自相关指标] --> B[Moran's I]
A --> C[Geary's C]
B --> D[正空间自相关]
C --> E[负空间自相关]
D --> F[空间聚集]
E --> G[空间分散]
F --> H[区域同质性]
G --> I[区域异质性]

### 3.1.2 局部空间自相关分析

局部空间自相关分析进一步细化了空间分布的局部特征。局部指标如局部Moran's I（LISA），可以揭示单个空间单元与其周围空间单元之间的空间关联性。通过LISA簇图，我们可以直观地看出哪些区域具有高值或低值的空间聚集特征，哪些区域具有空间异常值。这有助于理解局部的空间异质性和空间分布的复杂性。

graph LR
A[局部空间自相关分析] --> B[局部Moran's I]
B --> C[高-高聚集]
B --> D[低-低聚集]
B --> E[高-低异常]
B --> F[低-高异常]
C --> G[空间聚集同质]
D --> H[空间聚集同质]
E --> I[空间分散异质]
F --> J[空间分散异质]
G --> K[区域强正自相关]
H --> L[区域强负自相关]

## 3.2 空间热点分析

### 3.2.1 热点检测方法和工具

空间热点分析是指识别出空间数据中的热点区域，即统计学上显著的高值或低值聚集区域。常用的热点检测方法包括Getis-Ord Gi*等统计方法，它们能够识别出局部区域内的异常值和热点区域。通过热点检测工具，如GeoDa中的热点地图工具，研究人员能够创建热点地图，直观展示出空间分布的热点和冷点区域。

### 3.2.2 热点图的制作和解读

热点图是将热点分析结果通过地图形式直观展示的工具。在热点图中，可以通过颜色深浅来表示属性值的高低，颜色越深表示值越高或越低，形成明显的聚集区域。解读热点图时，需要注意避免过度解读或简化复杂的空间现象，要结合实际研究背景和数据的具体情况，结合其他统计分析方法进行综合判断。

## 3