SSIM在图像处理中的魔法：解锁图像质量提升的新境界

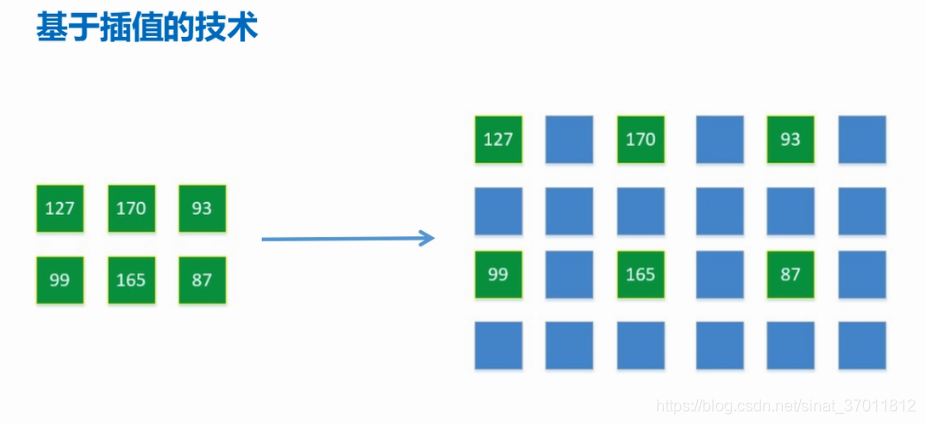
# 1. SSIM图像质量评估原理

SSIM（结构相似性）是一种图像质量评估指标，用于衡量两幅图像之间的相似程度。它基于人眼视觉系统对图像的感知特性，从亮度、对比度和结构三个方面来评估图像质量。

SSIM指标的计算公式如下：

SSIM(x, y) = (2μxμy + C1)(2σxy + C2) / ((μx^2 + μy^2 + C1)(σx^2 + σy^2 + C2))

其中：

* x、y：两幅待比较的图像
* μx、μy：x、y图像的平均值
* σx、σy：x、y图像的标准差
* σxy：x、y图像的协方差
* C1、C2：常数，用于稳定计算

# 2. SSIM在图像处理中的应用实践

### 2.1 SSIM图像增强

#### 2.1.1 直方图均衡化

**原理：**

直方图均衡化是一种图像增强技术，通过调整图像的像素分布，使图像的直方图更加均匀，从而提高图像的对比度和清晰度。

**步骤：**

1. 计算图像的直方图，即每个灰度值的像素数量。
2. 计算累积直方图，即每个灰度值以下所有像素数量的总和。
3. 将累积直方图归一化到[0, 1]的范围内。
4. 对于每个像素，根据其灰度值查找归一化累积直方图中的对应值，并将其作为新的灰度值。

**代码块：**

import cv2
import numpy as np

def histogram_equalization(image):
    """
    对图像进行直方图均衡化。

    参数：
        image: 输入图像。

    返回：
        均衡化后的图像。
    """

    # 计算直方图
    hist = cv2.calcHist([image], [0], None, [256], [0, 256])

    # 计算累积直方图
    cum_hist = np.cumsum(hist)

    # 归一化累积直方图
    cum_hist_normalized = cum_hist / cum_hist[-1]

    # 映射新的灰度值
    equalized_image = np.interp(image, np.arange(256), cum_hist_normalized)

    return equalized_image

**逻辑分析：**

* `cv2.calcHist`函数计算图像的直方图，并返回一个包含256个元素的数组，每个元素表示对应灰度值的像素数量。
* `np.cumsum`函数计算累积直方图，即每个灰度值以下所有像素数量的总和。
* `cum_hist_normalized`将累积直方图归一化到[0, 1]的范围内。
* `np.interp`函数根据每个像素的灰度值，在归一化累积直方图中查找对应的值，并将其作为新的灰度值。

#### 2.1.2 自适应直方图均衡化

**原理：**

自适应直方图均衡化是一种局部直方图均衡化技术，它将图像划分为小的子区域，并对每个子区域进行直方图均衡化。这可以避免全局直方图均衡化造成的过度增强或欠增强。

**步骤：**

1. 将图像划分为小的子区域。
2. 对每个子区域进行直方图均衡化。
3. 将均衡化后的子区域拼接在一起，形成均衡化后的图像。

**代码块：**

import cv2

def adaptive_histogram_equalization(image, block_size=32):
    """
    对图像进行自适应直方图均衡化。

    参数：
        image: 输入图像。
        block_size: 子区域大小。

    返回：
        均衡化后的图像。
    """

    # 划分子区域
    sub_images = [image[i:i+block_size, j:j+block_size] for i in range(0, image.shape[0], block_size) for j in range(0, image.shape[1], block_size)]

    # 对每个子区域进行直方图均衡化
    equalized_sub_images = [histogram_equalization(sub_image) for sub_image in sub_images]

    # 拼接均衡化后的子区域
    equalized_image = np.zeros_like(image)
    for i in range(0, image.shape[0], block_size):
        for j in range(0, image.shape[1], block_size):
            equalized_image[i:i+block_size, j:j+block_size] = equalized_sub_images[(i//block_size) * (image.shape[1]//block_size) + (j//block_size)]

    return equalized_image

**逻辑分析：**

* `[image[i:i+block_size, j:j+block_size] for i in range(0, image.shape[0], block_size) for j in range(0, image.shape[1], block_size)]`将图像划分为大小为`block_size`的子区域。
* `[histogram_equalization(sub_image) for sub_image in sub_images]`对每个子区域进行直方图均衡化。
* `np.zeros_like(image)`创建一个与原图像大小相同的新图像，并将其初始化为0。
* 循环将均衡化后的子区域拼接回原图像中。

# 3. SSIM在图像处理中的高级应用

### 3.1 SSIM图像融合

图像融合是将多幅图像融合成一幅图像的过程，融合后的图像包含了多幅图像的互补信息，可以提高图像的质量和信息丰富度。SSIM可以作为图像融合的质量评价指标，指导融合算法优化融合参数，获得更优质的融合图像。

#### 3.1.1 平均融合

平均融合是最简单的图像融合方法，它将多幅图像的像素值直接相加，再除以图像数量，得到融合后的图像。平均融合的优点是计算简单，但融合后的图像可能会出现过曝或欠曝的问题。

import cv2

# 加载多幅图像
img1 = cv2.imread('image1.jpg')
img2 = cv2.imread('image2.jpg')

# 平均融合
fused_img = cv2.addWeighted(img1,