多元统计分析中的因子分析：方法与实例的专业解读


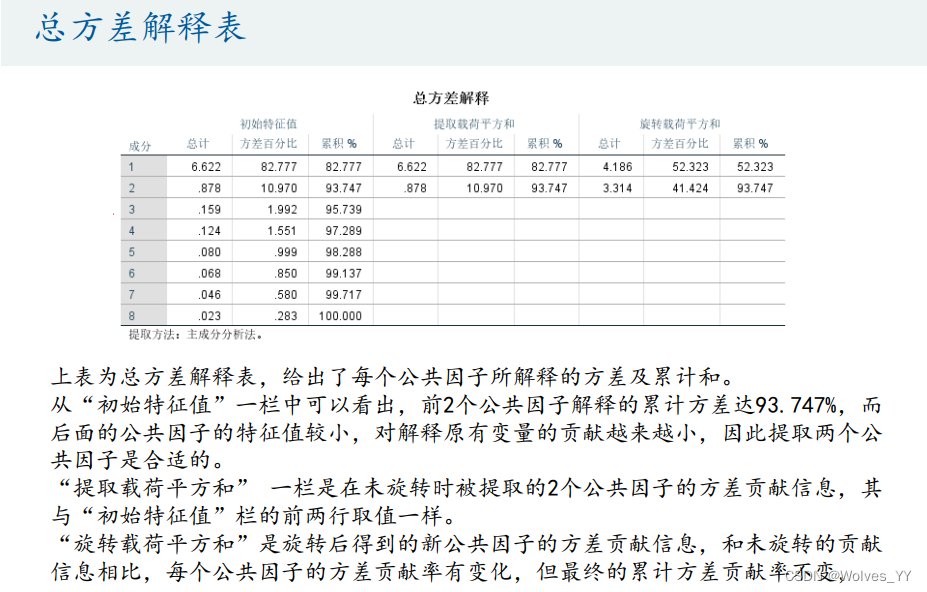
# 摘要
因子分析是一种重要的多变量统计技术，用于研究变量之间的内在关系结构。本文首先概述了因子分析方法，介绍了其理论基础、数学模型，以及因子分析的适用条件。随后，文章详细探讨了因子提取的准则、方法论和实践中如何使用统计软件进行操作，包括因子旋转与解释，以及结果验证。此外，文章还探讨了因子分析在多变量研究中的应用，并指出了探索性因子分析与验证性因子分析的区别。高级主题部分讨论了因子分析的局限性和常见误区。案例研究章节通过实际数据分析展示了因子分析的具体实施过程和结果解读。最后，本文展望了因子分析与其它统计技术的结合，以及在大数据环境下的发展方向。

# 关键字
因子分析；数学模型；适用条件；统计软件；因子旋转；模型验证；多变量研究；大数据分析

参考资源链接：[应用多元统计分析答案详解汇总高惠璇.pdf](https://wenku.csdn.net/doc/6412b48cbe7fbd1778d3ff95?spm=1055.2635.3001.10343)
# 1. 因子分析方法概述

## 1.1 因子分析的定义和目的

因子分析是一种降维技术，它通过识别具有较强关联性的变量中的共同因子，来解释观测变量之间的关系，并用较少的因子来描述原始数据的结构。该方法在统计学、心理学、市场研究等领域得到广泛应用，其目的在于数据简化、减少变量数目、揭示潜在的数据结构。

## 1.2 因子分析的流程概览

因子分析过程包括一系列的步骤，如数据检验、因子提取、因子旋转、以及因子得分的计算。在分析之初，需要进行数据的初步检验来评估其适合性；随后提取因子，常用的方法有主成分分析和主轴因子法；因子提取后，通过旋转方法来优化因子结构；最后，根据因子载荷矩阵来计算因子得分，并对因子进行解释。

## 1.3 因子分析的应用场景

因子分析在现实世界中的应用十分广泛，从学术研究到商业分析都扮演着重要角色。例如，在心理学研究中，它被用来确定问卷调查中的潜在心理特质；在市场研究中，用于识别影响消费者行为的关键因素；在生物学中，用于发现影响复杂表型的遗传因子。通过因子分析，研究者和分析人员能够获取比直接观察数据更深层次的信息。

# 2. 因子分析的理论基础

### 2.1 因子分析的数学模型

在这一部分，我们将探讨因子分析的核心概念及其数学基础。因子分析是一种统计方法，用于描述多个变量间的相互关系，通过较少的潜在变量（即因子）来解释变量之间的相关性。

#### 2.1.1 变量的共性和特殊性

要理解因子分析的数学模型，首先需掌握变量之间的共性和特殊性。共性是指变量间共享的那部分变异，而特殊性则是指每个变量特有的那部分变异。共性通过公共因子来解释，而特殊性通常被视为唯一因子或误差项。数学上，这可以表示为：
\[ x = \Lambda f + \Psi u + \epsilon \]
其中，\(x\) 表示观测变量，\(\Lambda\) 是因子载荷矩阵，\(f\) 是公共因子，\(\Psi\) 是特殊因子载荷矩阵，\(u\) 表示特殊因子，\(\epsilon\) 是误差项。

#### 2.1.2 因子得分和载荷的数学意义

因子得分和载荷是因子分析中的两个重要概念。因子载荷表示观测变量与公共因子之间的相关系数，其值的大小可以反映变量与因子之间关系的强度。数学上，因子载荷是变量协方差矩阵对角化后的特征向量。而因子得分则是对个体在每个因子上的值进行量化，用于预测个体在潜在变量上的位置。

### 2.2 因子分析的适用条件

因子分析的有效应用依赖于一定的前提条件，这些条件涉及数据的类型和结构。

#### 2.2.1 数据类型的适宜性分析

因子分析适用于连续性的度量变量，通常数据应满足一定的分布特性。例如，数据中不能有太多个别的异常值，否则会扭曲因子的提取。使用Kaiser-Meyer-Olkin (KMO) 测度和Bartlett's Test of Sphericity可以评估数据是否适合进行因子分析。

#### 2.2.2 样本量和变量关系的考量

因子分析需要足够的样本量来确保估计的稳定性和可靠性。一般来说，样本量应远大于变量数，具体比例没有统一的标准，但常见的是样本量至少是变量数的5倍至10倍。此外，变量之间应有足够相关性，以确保提取的因子是有意义的。

### 2.3 因子提取的方法论

因子提取是因子分析的核心过程，它涉及从原始变量中提取公共因子。

#### 2.3.1 主成分分析与因子分析的关系

在实际操作中，因子提取的常见方法包括主成分分析（PCA）和主轴因子法（PAF）。主成分分析更侧重于数据降维，而因子分析更侧重于数据结构的简化和潜在变量的发现。虽然两者在数学处理上相似，但最终目的和后续步骤存在区别。

#### 2.3.2 因子提取的准则和步骤

因子提取通常遵循以下步骤：
1. 评估数据是否适合进行因子分析。
2. 选择因子提取方法。
3. 确定因子的数量。常用的方法包括特征值大于1规则和累计方差解释百分比。
4. 进行因子提取并得出因子载荷矩阵。
5. 进行因子旋转以提高因子的可解释性。

为了进一步深入理解因子分析理论基础，我们还可以参考以下表格和代码块。

#### 表格示例：因子提取方法对比

| 特点 | 主成分分析 | 主轴因子法 |
| --- | --- | --- |
| 目的 | 数据降维 | 结构简化和潜在变量发现 |
| 提取依据 | 特征值大于1 | 累计方差解释百分比 |
| 过程 | 直接提取 | 逐步迭代 |

接下来，我们来演示一个因子提取的代码示例。在R语言中，因子分析通常使用`factanal()`函数来完成：

# 安装并载入需要的包
if (!require("psych")) install.packages("psych")
library(psych)

# 假设dataMatrix是已经准备好的数据集
dataMatrix <- matrix(rnorm(100), ncol=5)

# 进行因子分析
factanalResult <- factanal(dataMatrix, factors=2, rotation="varimax")

# 输出结果
print(factanalResult)

上述代码中，`factanal()`函数用于执行因子分析，参数`factors=2`指定了提取的因子数量，`rotation="varimax"`用于指定旋转方法以提高因子的解释性。输出的结果包含了因子载荷矩阵和因子得分等信息。