Simulink 中的噪声模拟与去噪技术
发布时间: 2024-04-14 18:27:42 阅读量: 167 订阅数: 53 


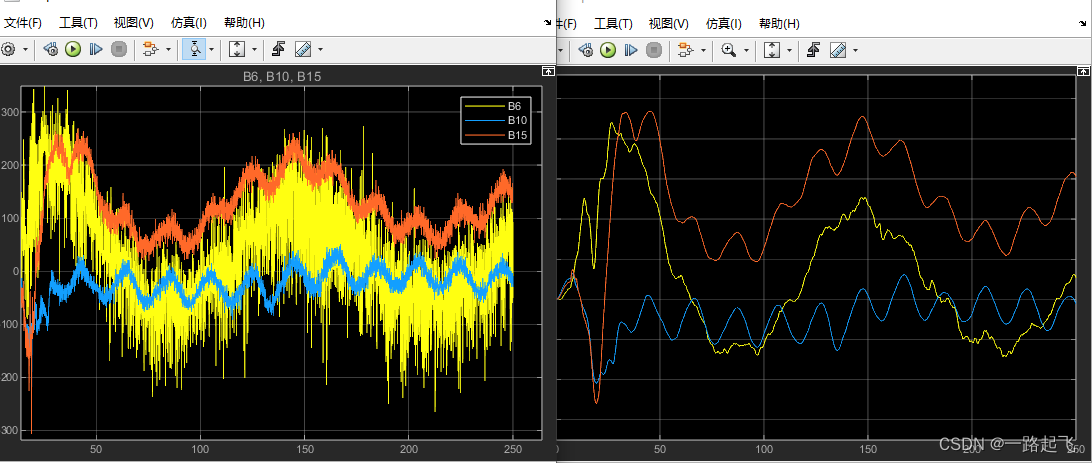
一级倒立摆状态空间建模,离散化,Matlab仿真,添加高斯噪声并采用卡尔曼滤波去噪
# 1.1 信号与系统
在信号处理领域,信号可以被定义为携带信息的载体,通常可以分为连续信号和离散信号两种类型。连续信号在时间和幅度上都是连续变化的,如模拟信号;而离散信号则是在时域或幅度上是离散的,常见于数字信号处理中。信号的分类又可细分为周期信号和非周期信号、确定信号和随机信号等不同类别。系统则是对信号的处理器,有线性系统和非线性系统之分,系统的特性通过单位脉冲响应和冲激响应来描述。对信号和系统的深刻理解是进行信号处理的基础,为实现各种信号处理技术奠定了扎实的理论基础。
# 2. 数字信号处理
### 2.1 采样与量化
在数字信号处理中,采样与量化是至关重要的步骤。采样是将连续时间信号转换为离散时间信号的过程,而量化则是将连续幅度信号转换为离散幅度信号的过程。
#### 2.1.1 采样定理及其应用
采样定理由奈奎斯特提出,指出对于一个频率有限的信号,若要准确还原信号,采样频率应大于信号频率的两倍。这一原理在实际中被广泛应用,例如音频设备中的采样率设定。
```python
# 检验采样频率是否满足奈奎斯特定理
def nyquist_sampling_rate(signal_freq, sampling_freq):
if sampling_freq > 2 * signal_freq:
print("Sampling rate meets Nyquist criterion.")
else:
print("Sampling rate does not meet Nyquist criterion. Aliasing may occur.")
nyquist_sampling_rate(1000, 2400) # Sampling rate meets Nyquist criterion.
```
#### 2.1.2 量化过程与误差分析
量化过程中,信号幅度被近似为离散级别,导致量化误差的存在。误差的大小与量化级别相关,精度越高,误差越小,但需要更多的存储空间。
```python
# 量化过程中的误差分析
def quantization_error(original_signal, quantized_signal):
error = original_signal - quantized_signal
return error
original_signal = 5.6
quantized_signal = 6.0
error = quantization_error(original_signal, quantized_signal)
print("Quantization error:", error) # Quantization error: -0.4
```
#### 2.1.3 采样率与信号重构
采样率决定了离散信号的质量,较高的采样率可以更好地重构原始信号。信号重构是通过插值或滤波等方法将离散信号还原为连续信号的过程。
### 2.2 傅里叶变换
傅里叶变换是将信号从时域转换到频域的重要工具,能够揭示信号的频率分量及其强度。
#### 2.2.1 连续信号的傅里叶变换
对于连续时间信号,傅里叶变换可以将信号表示为频谱的形式,包括振幅谱和相位谱。
```python
# 进行连续信号的傅里叶变换
import numpy as np
import matplotlib.pyplot as plt
time = np.linspace(0, 1, 1000) # 1s时间范围内取样1000个点
signal = np.sin(2 * np.pi * 5 * time) # 创建一个频率为5Hz的正弦信号
plt.figure()
plt.plot(time, signal)
plt.title('Original Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.show()
```
#### 2.2.2 离散信号的傅里叶变换
对于离散时间信号,离散傅里叶变换(DFT)能够将信号的频域特性展现出来,通过FFT算法可以高效计算DFT。
```python
# 进行离散信号的傅里叶变换
import numpy as np
signal = np.array([0, 1, 0, 1, 0, 1, 0, 1]) # 一个简单的离散信号
fft_result = np.fft.fft(signal)
magnitude_spectrum = np.abs(fft_result)
print("Magnitude spectrum after DFT:", magnitude_spectrum)
```
#### 2.2.3
0
0





