模拟电路中的滤波器技术


# 摘要
滤波器是模拟电路中用于信号处理的关键组件，其基础概念和理论在电子工程领域至关重要。本文首先介绍了滤波器在模拟电路中的基础概念，并对其理论进行了详解，包括滤波器的基本原理、数学模型及其设计方法。接着，本文转入滤波器设计的实践环节，探讨了设计工具和实际电路搭建技巧，同时提供了故障分析与维修的方法。高级应用部分则涉及多功能复合滤波器设计、数字信号处理中的滤波器技术以及特殊领域中的滤波器应用。最后，本文对滤波器技术的前沿探索进行了展望，包括微波和射频滤波器设计、滤波器的集成化和模块化趋势以及滤波器材料和制造工艺的创新。通过系统阐述滤波器从基础理论到实际应用再到技术前沿的全方位知识，本文为读者提供了全面的技术指南。

# 关键字
滤波器；模拟电路；数学模型；设计方法；故障分析；数字信号处理；微波射频技术；集成化模块化；新材料应用；制造工艺

参考资源链接：[优化差分ADC前端抗混叠RC滤波器设计：提高信噪比与稳定性](https://wenku.csdn.net/doc/6412b4dbbe7fbd1778d41120?spm=1055.2635.3001.10343)
# 1. 滤波器在模拟电路中的基础概念

在模拟电路设计中，滤波器是一项关键的电子元件，它能够选择性地允许特定频率范围的信号通过，同时抑制或过滤掉不需要的频率。理解滤波器的基本概念对于设计高效的模拟电路至关重要。本章将简单介绍滤波器在模拟电路中的作用，以及它们的类型和基本工作原理。

## 1.1 信号滤波的目的和作用

滤波器最根本的功能是实现信号的频率选择性。在通信、音频处理、数据采集等多种应用中，滤波器能够分离信号中的有用成分和噪声。例如，在接收器中，滤波器可帮助去除相邻频道的干扰；在音频系统中，滤波器可用于加强或减弱某些频率范围的响应，以改善音质。

## 1.2 滤波器的分类及其特点

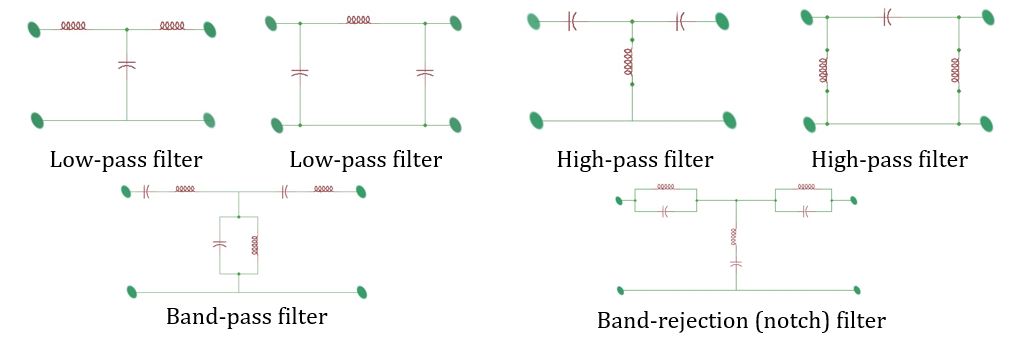
滤波器根据其工作频率和设计原理，大致可分为低通、高通、带通和带阻四种基本类型。每种类型都有其特定的应用场景和设计要求。例如，低通滤波器允许低于某个截止频率的信号通过，而阻止高频信号；相反，高通滤波器则允许高于截止频率的信号通过。带通滤波器和带阻滤波器则分别允许或阻止特定频率范围内的信号。

理解这些基础概念将为深入学习后续章节中更高级的滤波器设计与应用打下坚实的基础。

# 2. 滤波器理论详解

## 2.1 滤波器的基本原理

### 2.1.1 信号滤波的目的和作用

滤波器是电子系统中不可或缺的组件，它的基本目的是通过特定的频率范围，抑制或衰减不需要的信号成分。在信号处理过程中，滤波器扮演着至关重要的角色，用于降低噪声、提取有用信号以及实现信号的频谱分析等。滤波器的作用可以从以下几个方面进行详细阐述：

- **噪声抑制**：噪声往往在高频部分，滤波器可以设计为低通滤波器，允许低频信号通过而衰减高频噪声。
- **信号分离**：在多信号混合传输的场合，滤波器能够选择性地提取特定频率的信号，实现信号的有效分离。
- **信号整形**：通过使用滤波器可以平滑或整形信号，例如在模拟数字转换前使用低通滤波器减少混叠现象。

### 2.1.2 滤波器的分类及其特点

滤波器按照工作原理和结构可以分为多种类型，常见的有无源滤波器和有源滤波器、低通滤波器、高通滤波器、带通滤波器和带阻滤波器等。各类滤波器在性能和应用场景上具有不同的特点：

- **无源滤波器**：由电阻器、电容器和电感器组成，不需要外部电源供电。其特点是结构简单、成本低，但功率处理能力有限。
- **有源滤波器**：在无源滤波器的基础上增加了有源元件，如晶体管或运算放大器。有源滤波器能够提供增益，适合低电平信号的滤波处理。
- **低通滤波器**：允许低于某个截止频率的信号通过，高于截止频率的信号则被衰减。常用于抗混叠滤波。
- **高通滤波器**：与低通滤波器相反，它允许高于某个截止频率的信号通过，低于该频率的信号被衰减。在声音处理中，高通滤波器可以用来去除低频噪声。
- **带通滤波器**：只允许某个特定频段范围内的信号通过。在通信系统中，带通滤波器用于提取调制信号。
- **带阻滤波器**：也称陷波器，它阻隔特定频段内的信号，而允许此频段外的信号通过。常用于消除特定频率的干扰。

## 2.2 滤波器的数学模型

### 2.2.1 传递函数与频率响应

滤波器的数学描述通常通过传递函数来表示，它表达了输入信号与输出信号之间的数学关系。滤波器的传递函数H(s)（其中s为复频率变量）描述了滤波器如何影响通过它的信号。

- **频率响应**：当传递函数中的s用jω(j是虚数单位，ω是角频率)替代时，我们得到H(jω)，即频率响应函数。频率响应揭示了滤波器对不同频率信号的放大或衰减程度。

为了进一步了解滤波器的特性，可以通过绘制其幅度响应和相位响应来观察：

- **幅度响应**：表示滤波器对不同频率信号的增益或衰减程度，通常以分贝（dB）为单位表示。
- **相位响应**：描述滤波器如何改变通过信号的相位，这是影响信号波形的另一个重要因素。

### 2.2.2 滤波器的设计参数和性能指标

在设计滤波器时，必须考虑一系列的性能指标和设计参数，主要包括：

- **截止频率（fc）**：定义为滤波器传输函数幅度下降到其最大值的0.707（-3dB）时的频率。
- **带宽（BW）**：对于带通和带阻滤波器来说，是信号通过的频率范围的宽度。
- **阶数（n）**：滤波器的阶数决定了频率响应曲线的斜率，也就是滤波器的频率选择性。
- **品质因数（Q）**：它反映了滤波器在截止频率附近的选频能力。Q值越高，滤波器的选择性越好，但可能会引起更陡峭的相位变化。
- **通带和阻带波纹**：分别指通带和阻带允许的最大幅度变化。

## 2.3 常见滤波器设计方法

### 2.3.1 巴特沃斯、切比雪夫和贝塞尔滤波器设计

不同的滤波器设计方法各有特点，适应于不同的应用需求。其中，巴特沃斯、切比雪夫和贝塞尔是三种常见的设计方法：

- **巴特沃斯滤波器**：具有最平坦的通带幅度响应，适用于对相位失真要求不高的场合。
- **切比雪夫滤波器**：在通带或阻带中有等纹波特性，可以实现更陡峭的截止斜率。
- **贝塞尔滤波器**：其特点是具有最平滑的群延迟响应，适用于脉冲信号，因为它能保持信号波形的完整性。

### 2.3.2 高阶滤波器的级联设计技巧

高阶滤波器可以通过将多个低阶滤波器级联来设计。级联设计方法的优点在于：

- **设计灵活性**：可以选择不同类型的低阶滤波器进行组合，以满足不同的性能要求。
- **易于实现**：单个低阶滤波器更容易设计和调试，级联后的整体性能可通过单个环节的微调来优化。
- **模块化设计**：便于进行模块化生产和测试，提高生产效率和可维护性。

接下来，将具体介绍如何通过级联二阶滤波器的方法来构建一个高阶滤波器，并分析其设计过程和优化策略。

# 3. 滤波器设计实践

## 3.1 滤波器设计的软件工具

在滤波器设计的工程实践中，软件工具的应用已成为不可或缺的一部分。使用这些工具可以极大地提高设计效率和精确度，同时还能帮助设计者进行复杂分析和仿真。本节将介绍两种常用的软件工具：SPICE仿真和计算机辅助设计（CAD）工具，并探讨它们在滤波器设计中的应用。

### 3.1.1 使用SPICE进行滤波器仿真

SPICE（Simulation Program with Integrated Circuit Emphasis）是一种用于电路仿真和分析的通用模拟程序。它能模拟各种电路，包括放大器、振荡器、滤波器和其他复杂的电子电路。使用SPICE进行滤波器仿真可以让设计者在实际搭建电路之前，进行详尽的分析和测试。