【R语言时间序列分析】：alabama包的关键作用与应用

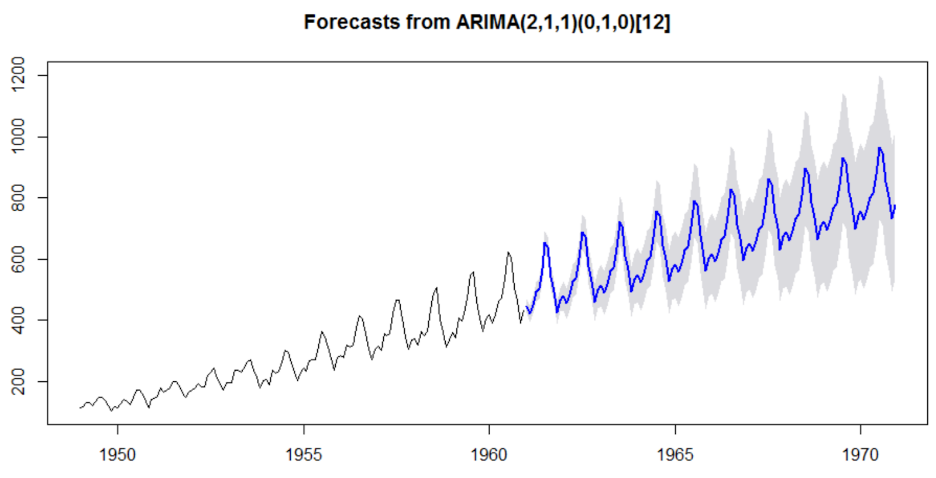
# 1. R语言时间序列分析简介

R语言自诞生以来就因其强大的统计分析和图形展现能力而在数据分析领域广受欢迎。时间序列分析作为数据分析的一个重要分支，在经济学、金融、生物学等多个领域中有着广泛的应用。本章节将为读者提供一个关于时间序列分析的基础性介绍，旨在为后文深入探讨`alabama`包在时间序列建模中的应用打下坚实的基础。

## 1.1 时间序列分析的定义与重要性

时间序列分析是通过分析按时间顺序排列的数据点，来理解数据随时间变化的模式和趋势的一种统计方法。在现代社会中，时间序列数据无处不在，而正确地理解和预测这些数据的走势可以帮助做出更为明智的决策。

## 1.2 时间序列分析的组成要素

一个时间序列通常由三个主要部分组成：趋势（Trend）、季节性（Seasonality）和不规则波动（Irregular）。理解这些要素对于构建和评估时间序列模型至关重要。

## 1.3 时间序列分析的基本步骤

时间序列分析通常遵循以下步骤：数据收集、数据预处理、模型选择、模型拟合、模型评估、预测以及决策制定。本章的后续部分和后续章节将围绕这些步骤逐一展开详细讨论。

# 2. alabama包的基础知识

## 2.1 时间序列分析的理论基础

### 2.1.1 时间序列的组成要素
时间序列是由同一统计指标的观察值按照时间的先后顺序排列而形成的一组数据序列。它通常包含四个基本要素：

- **趋势(Trend)**: 指时间序列的总体向上或向下的走向，反映了数据随时间变化的长期方向。
- **季节性(Seasonality)**: 在固定的时间间隔内重复出现的周期性波动。例如，零售业在圣诞节期间的销售量会有季节性的上升。
- **周期性(Cyclicality)**: 指时间序列中超过一年的波动模式，这通常与经济周期相关。
- **随机成分(Noise)**: 是不可预测的、不规则的成分，它反映了观测值中无法被趋势、季节性或周期性解释的波动。

理解这些成分对于正确建模和预测至关重要。时间序列分析试图从历史数据中分离和理解这些成分，以便对未来值进行合理预测。

### 2.1.2 时间序列分析的目的和方法
时间序列分析的目的是：

- **描述性分析**：可视化数据，识别数据中的模式和结构。
- **预测未来值**：基于历史数据预测未来时间点的值。
- **异常检测**：识别数据中的异常情况，可能表示某种特殊的事件或错误。
- **数据解释**：通过时间序列模型解释数据中的相关性和因果关系。

时间序列分析的方法包括：

- **移动平均(Moving Average, MA)**：通过平均一系列连续的观测值来平滑数据，并识别趋势。
- **指数平滑(Exponential Smoothing)**：给予近期观测值更高的权重，使得模型对新数据更加敏感。
- **ARIMA模型**：自回归积分滑动平均模型，适用于许多时间序列数据，可以处理非平稳时间序列。
- **季节性分解(Seasonal Decomposition)**：将时间序列分解为趋势、季节性和随机成分。

## 2.2 alabama包概述

### 2.2.1 alabama包的功能和特点
`alabama`包在R语言中提供了一组工具来拟合各种形式的优化问题，尤其适用于参数估计问题。在时间序列分析中，`alabama`包可以用来进行极大似然估计，特别是在模型选择和参数估计阶段。

包的主要特点包括：

- **稳健的优化算法**：包括局部搜索和全局优化算法，适用于复杂的非线性模型。
- **灵活的接口**：可以处理多种参数估计问题，包括那些需要约束优化的问题。
- **广泛的应用**：不仅可以用于时间序列，还可以用于经济学、统计学等领域的优化问题。

### 2.2.2 安装与配置alabama包
安装`alabama`包非常直接，可以通过R的标准包安装命令完成：

install.packages("alabama")

安装完成后，可以通过如下方式加载包：

library(alabama)

## 2.3 基于alabama包的数据探索

### 2.3.1 数据预处理
在时间序列分析中，数据预处理是至关重要的一步。数据预处理包括数据清洗、数据转换和数据标准化等。使用`alabama`包进行数据预处理，可以处理其中的非线性约束问题，例如对数转换等。

假设我们有以下时间序列数据：

data <- c(1.4, 1.6, 1.5, 1.8, 1.9, 2.0, 2.3, 2.4, 2.2, 2.5, 2.7, 2.9)

我们想要拟合一个线性模型，并对系数进行约束。`alabama`包中的`aoptim()`函数允许我们指定约束条件：

# 定义一个目标函数
objective <- function(x) {
  sum((data - x[1] - x[2] * (1:length(data)))^2)
}

# 指定约束条件
constr <- list()
constr$equals <- c(NA)  # 相当于没有等式约束
constr$less <- c(0)     # 系数的下界是0

# 使用aoptim进行约束优化
fit <- aoptim(par = c(1, 1), fn = objective, lower = c(-Inf, 0), 
              control = list(reltol = 1e-9), constr = constr)

# 输出优化结果
print(fit$par)

### 2.3.2 数据可视化技巧
在进行时间序列分析时，可视化数据有助于我们直观地理解数据特征。`alabama`包本身不提供绘图功能，但我们可以将拟合得到的模型参数应用于绘图函数来展示结果。

例如，我们可以使用R基础函数`plot()`来绘制原始数据和拟合的模型：

# 假设fit$par包含了模型参数
coefficients <- fit$par
plot(data, type = "l", col = "blue", main = "Time Series Data and Fitted Model", xlab = "Time", ylab = "Value")
lines(1:length(data), coefficients[1] + coefficients[2] *