单片机程序设计中的数据结构与算法：高效编程的利器

# 1. 单片机程序设计基础

单片机是一种集成在单个芯片上的微型计算机，它具有处理数据、控制外设和存储信息的能力。单片机程序设计是利用单片机的特性，编写程序来实现特定功能。

单片机程序设计的基础知识包括：

- **单片机架构：**了解单片机的内部结构，包括CPU、存储器、外设和总线。
- **汇编语言：**掌握汇编语言的语法和指令集，用于编写单片机程序。
- **C语言：**了解C语言在单片机程序设计中的应用，包括数据类型、变量、函数和结构体。
- **单片机开发环境：**熟悉单片机开发环境，包括编译器、仿真器和调试器。

# 2. 数据结构在单片机程序设计中的应用

在单片机程序设计中，数据结构扮演着至关重要的角色。它提供了一种组织和管理数据的有效方式，从而简化程序设计，提高代码效率和可维护性。本章将深入探讨单片机程序设计中常用的数据结构，包括数组、链表和队列，并分析其在实际应用中的优势和局限性。

### 2.1 数组：单片机程序设计中的数据存储利器

数组是一种线性数据结构，它存储相同数据类型的元素，并通过索引值访问。在单片机程序设计中，数组广泛用于存储数据，例如传感器读数、控制参数和状态信息。

#### 2.1.1 一维数组的定义和使用

一维数组是一种最简单的数组类型，它存储相同数据类型的元素，并使用单个索引值访问。例如，以下代码定义了一个存储 10 个整数元素的一维数组：

int array[10];

要访问数组中的元素，可以使用索引值，如下所示：

array[0] = 10;
int value = array[5];

一维数组在单片机程序设计中非常有用，因为它提供了对数据的快速和直接的访问。然而，它也存在一些局限性，例如，它的大小是固定的，并且无法动态地添加或删除元素。

#### 2.1.2 二维数组的定义和使用

二维数组是一种更高级的数据结构，它存储相同数据类型的元素，并使用两个索引值访问。这使得它非常适合存储表格或矩阵等多维数据。例如，以下代码定义了一个存储 5 行 10 列整数元素的二维数组：

int array[5][10];

要访问二维数组中的元素，可以使用两个索引值，如下所示：

array[2][3] = 15;
int value = array[1][7];

二维数组在单片机程序设计中非常有用，因为它提供了对多维数据的有效组织和访问。然而，它也存在一些局限性，例如，它的存储空间需求更大，并且访问元素时需要更多的计算开销。

### 2.2 链表：单片机程序设计中的动态数据结构

链表是一种非线性数据结构，它存储数据元素，每个元素包含一个数据值和一个指向下一个元素的指针。这使得链表非常适合存储动态数据，例如队列、栈和树。

#### 2.2.1 链表的定义和结构

链表的基本元素是节点，它包含一个数据值和一个指向下一个节点的指针。例如，以下代码定义了一个链表节点：

struct node {
    int data;
    struct node *next;
};

链表通过一个头指针指向第一个节点，并通过尾指针指向最后一个节点。这使得链表可以动态地添加或删除元素，而无需重新分配内存。

#### 2.2.2 链表的插入、删除和遍历

链表中的元素可以通过以下方式插入、删除和遍历：

* **插入：**要插入一个元素，创建一个新的节点，并将它的指针指向下一个元素。然后，更新前一个元素的指针，使其指向新节点。
* **删除：**要删除一个元素，找到它的前一个元素，并将它的指针指向被删除元素的下一个元素。
* **遍历：**要遍历链表，从头指针开始，并沿着每个节点的指针移动，直到到达尾指针。

链表在单片机程序设计中非常有用，因为它提供了对动态数据的有效组织和访问。然而，它也存在一些局限性，例如，它需要更多的内存开销，并且访问元素时需要更多的计算开销。

### 2.3 队列：单片机程序设计中的先进先出数据结构

队列是一种先进先出（FIFO）数据结构，它存储数据元素，并按照先进先出的顺序访问它们。这使得队列非常适合存储需要按顺序处理的数据，例如消息、任务和事件。

#### 2.3.1 队列的定义和实现

队列可以通过数组或链表实现。数组实现使用一个固定大小的数组来存储元素，而链表实现使用一个链表来存储元素。以下代码使用数组实现了队列：

#define QUEUE_SIZE 10

int queue[QUEUE_SIZE];
int head = 0;
int tail = 0;

void enqueue(int data) {
    if ((tail + 1) % QUEUE_SIZE == head) {
        // 队列已满
    } else {
        queue[tail] = data;
        tail = (tail + 1) % QUEUE_SIZE;
    }
}

int dequeue() {
    if (head == tail) {
        // 队列已空
    } else {
        int data = queue[head];
        head = (head + 1) % QUEUE_SIZE;
        return data;
    }
}

#### 2.3.2 队列的应用场景

队列在单片机程序设计中非常有用，因为它提供了对先进先出数据的有效组织和访问。它可以用于各种应用场景，例如：

* 消息传递：队列可以存储待发送或接收的消息。
* 任务调度：队列可以存储待执行的任务。
* 事件处理：队列可以存储待处理的事件。

# 3. 算法在单片机程序设计中的应用

### 3.1 排序算法：单片机程序设计中的数据整理利器

排序算法是单片机程序设计中常用的算法，用于将数据按照一定的顺序排列。在单片机程序设计中，排序算法主要用于整理数据、查找数据和优化数据存储。

#### 3.1.1 冒泡排序算法

冒泡排序算法是一种简单的排序算法，其原理是逐一对相邻元素进行比较，如果顺序不正确，则交换这两个元素。重复这个过程，直到所有元素都按顺序排列。

void bubble_sort(int *arr, int len) {
    for (int i = 0; i < len - 1; i++) {
        for (int j = 0; j < len - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

**逻辑分析：**

* 外层循环 `i` 遍历数组，表示已排序元素的个数。
* 内层循环 `j` 遍历未排序元素，比较相邻元素是否需要交换。
* 如果 `arr[j]` 大于 `arr[j + 1]`，则交换这两个元素。

#### 3.1.2 快速排序算法

快速排序算法是一种高效的排序算法，其原理是将数组划分为两个子数组，一个子数组包含比基准值小的元素，另一个子数组包含比基准值大的元素。然后递归地对两个子数组进行排序。

void quick_sort(int *arr, int left, int right) {
    if (left < right) {
        int pivot = arr[right];
        int i = left - 1;
        for (int j = left; j < right; j++) {
            if (arr[j] < pivot) {
                i++;
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
        int new_pivot = i + 1;
        int temp = arr[new_pivot];
        arr[new_pivot] = arr[right];
        arr[right] = temp;
        quick_sort(arr, left, new_pivot - 1);
        quick_sort(arr, new_pivot + 1, right);
    }
}

**逻辑分析：**

* `left` 和 `right` 表示子数组的左右边界。
* 选择 `arr[right]` 作为基准值。
* 循环遍历数组，将比基准值小的元素移动到基准值左侧。
* 将基准值移动到正确的位置。
* 递归地对两个子数组进行排序。

### 3.2 搜索算法：单片机程序设计中的数据查找利器

搜索算法是单片机程序设计中常用的算法，用于在数据集合中查找特定元素。在单片机程序设计中，搜索算法主要用于查找数据、匹配数据和优化数据访问。

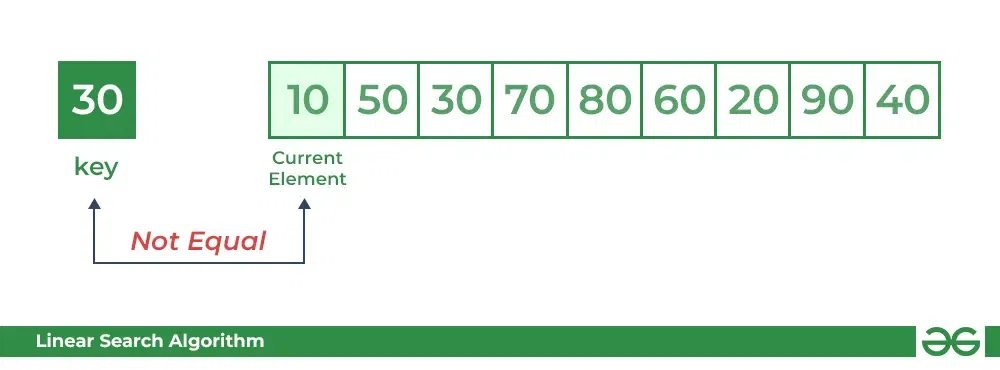
#### 3.2.1 线性搜索算法

线性搜索算法是一种简单的搜索算法，其原理是逐个遍历数据集合，直到找到目标元素或遍历完整个数据集合。

int linear_search(int *arr, int len, int target) {
    for (int i = 0; i < len; i++) {
        if (arr[i] == target) {
            return i;
        }
    }
    return -1;
}

**逻辑分析：**

* 循环遍历数组，比较每个元素是否等于目标元素。
* 如果找到目标元素，则返回其索引。
* 如果遍历完整个数组都没有找到目标元素，则返回 -1。

#### 3.2.2 二分查找算法

二分查找算法是一种高效的搜索算法，其原理是将数据集合划分为两个子集合，然后根据目标元素与子集合的中间元素比较，缩小搜索范围。

int binary_search(int *arr, int len, int target) {
    int left = 0;
    int right = len - 1;
    while (left <= right) {
        int mid = (left + right) / 2;
        if (arr[mid] == target) {
            return mid;
        } else if (arr[mid] < target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    return -1;
}

**逻辑分析：**

* `left` 和 `right` 表示子集合的左右边界。
* 计算子集合的中间元素 `mid`。
* 比较目标元素与中间元素。
* 根据比较结果调整 `left` 或 `right` 的值，缩小搜索范围。
* 重复上述步骤，直到找到目标元素或搜索范围为空。

### 3.3 哈希算法：单片机程序设计中的数据存储利器

哈希算法是一种将数据映射到固定大小数组的算法，其原理是根据数据生成一个哈希值，然后将数据存储在哈希值对应的数组位置。哈希算法在单片机程序设计中主要用于快速查找数据、优化数据存储和提高数据访问效率。

#### 3.3.1 哈希算法的原理和实现

哈希算法的原理是将数据映射到一个固定大小的数组，称为哈希表。哈希表中的每个位置称为一个桶。数据通过哈希函数生成一个哈希值，然后将数据存储在哈希值对应的桶中。

int hash_function(int key) {
    return key % TABLE_SIZE;
}

**逻辑分析：**

* `key` 是要哈希的数据。
* `TABLE_SIZE` 是哈希表的大小。
* 哈希函数将 `key` 映射到 `0` 到 `TABLE_SIZE - 1` 之间的整数。

#### 3.3.2 哈希算法在单片机程序设计中的应用

哈希算法在单片机程序设计中可以用于快速查找数据。例如，可以通过哈希函数将数据映射到哈希表，然后通过哈希值直接访问数据。这比线性搜索算法要高效得多。

# 4. 单片机程序设计中的数据结构与算法实战

### 4.1 数据结构在单片机程序设计中的实际应用

#### 4.1.1 数组在单片机程序设计中的应用实例

**应用场景：**存储多个相同数据类型的数据，如传感器采集的数据、控制参数等。

**代码示例：**

// 定义一个存储 10 个整数的数组
int data[10];

// 存储数据
for (int i = 0; i < 10; i++) {
    data[i] = i + 1;
}

// 访问数据
for (int i = 0; i < 10; i++) {
    printf("data[%d] = %d\n", i, data[i]);
}

**逻辑分析：**

* 定义一个名为 `data` 的数组，大小为 10，用于存储整数。
* 使用 `for` 循环将数据存储到数组中。
* 再次使用 `for` 循环访问数组中的数据并打印到控制台。

#### 4.1.2 链表在单片机程序设计中的应用实例

**应用场景：**存储动态变化的数据，如任务队列、消息队列等。

**代码示例：**

// 定义链表节点结构
typedef struct node {
    int data;
    struct node *next;
} node_t;

// 定义链表头节点
node_t *head = NULL;

// 插入节点
void insert_node(int data) {
    node_t *new_node = malloc(sizeof(node_t));
    new_node->data = data;
    new_node->next = head;
    head = new_node;
}

// 删除节点
void delete_node(int data) {
    node_t *current = head;
    node_t *prev = NULL;

    while (current != NULL) {
        if (current->data == data) {
            if (prev == NULL) {
                head = current->next;
            } else {
                prev->next = current->next;
            }
            free(current);
            break;
        }
        prev = current;
        current = current->next;
    }
}

// 遍历链表
void print_list() {
    node_t *current = head;
    while (current != NULL) {
        printf("%d ", current->data);
        current = current->next;
    }
    printf("\n");
}

**逻辑分析：**

* 定义链表节点结构，包括数据和指向下一个节点的指针。
* 定义链表头节点，指向链表的第一个节点。
* `insert_node` 函数用于插入一个新节点到链表头部。
* `delete_node` 函数用于删除一个指定数据的节点。
* `print_list` 函数用于遍历链表并打印每个节点的数据。

### 4.2 算法在单片机程序设计中的实际应用

#### 4.2.1 排序算法在单片机程序设计中的应用实例

**应用场景：**对数据进行排序，如传感器数据排序、任务优先级排序等。

**代码示例：**

// 冒泡排序算法
void bubble_sort(int *arr, int len) {
    for (int i = 0; i < len - 1; i++) {
        for (int j = 0; j < len - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

**逻辑分析：**

* 冒泡排序算法通过比较相邻元素并交换位置，将最大的元素逐个移到数组末尾。
* 外层循环控制排序的趟数，内层循环比较相邻元素。
* 如果相邻元素顺序错误，则交换它们的顺序。

#### 4.2.2 搜索算法在单片机程序设计中的应用实例

**应用场景：**在数据中查找特定元素，如查找任务队列中的特定任务、查找传感器数据中的最大值等。

**代码示例：**

// 线性搜索算法
int linear_search(int *arr, int len, int target) {
    for (int i = 0; i < len; i++) {
        if (arr[i] == target) {
            return i;
        }
    }
    return -1;
}

**逻辑分析：**

* 线性搜索算法从数组开头逐个比较元素，直到找到目标元素或遍历完整个数组。
* 如果找到目标元素，则返回其索引，否则返回 -1。

# 5. 提升单片机程序设计效率

在单片机程序设计中，数据结构的选择和优化对程序的效率至关重要。通过合理选择数据结构和优化其存储方式，可以显著提升程序的性能。

### 5.1.1 数据结构的选择与优化

在选择数据结构时，需要考虑以下因素：

- **数据类型：**数据结构应与存储的数据类型相匹配，例如整数数组、浮点链表等。
- **访问模式：**根据程序对数据的访问模式选择合适的数据结构，例如顺序访问使用数组，随机访问使用链表。
- **存储空间：**考虑单片机有限的存储空间，选择空间利用率高的数据结构。

### 5.1.2 数据结构的存储优化

除了选择合适的数据结构外，还可以通过以下方式优化其存储：

- **紧凑存储：**使用位域、联合等技术将不同类型的数据紧凑地存储在一起，节省空间。
- **指针优化：**使用指针代替实际数据，避免冗余存储，节省空间。
- **内存对齐：**按照数据类型对齐数据，提高访问效率。

// 紧凑存储示例
typedef struct {
    uint8_t age : 4;
    uint8_t gender : 1;
    uint8_t height : 7;
} Person;

// 指针优化示例
typedef struct {
    char *name;
    uint8_t age;
} Student;

通过优化数据结构的选择和存储方式，可以有效减少程序的内存占用，提升运行效率。