信息论基础第二版：深入探讨复杂问题，揭秘解决之道


# 摘要
信息论是通信科学与计算机科学交叉领域的重要理论基础，其起源和发展推动了现代通信技术、数据处理和信息安全等多个方面。本文首先介绍了信息论的起源与发展历程，接着深入探讨了信息论中的基本概念与原理，如信息的度量、信道容量、编码定理以及数据压缩技术。随后，本文详述了信息论在计算机科学、机器学习与人工智能、现代通信系统中的应用，阐述了其在算法复杂度、加密技术、深度学习、自然语言处理以及5G通信中的关键作用。最后，本文展望了信息论的新进展与挑战，尤其是跨学科融合的创新以及在复杂系统研究中的应用前景。

# 关键字
信息论；信息熵；信道容量；数据压缩；机器学习；5G通信；信息安全

参考资源链接：[信息论基础第二版完整答案](https://wenku.csdn.net/doc/6412b70dbe7fbd1778d48eb4?spm=1055.2635.3001.10343)
# 1. 信息论的起源与发展

信息论作为一门研究信息传输和处理的科学，由克劳德·香农（Claude Shannon）在1948年提出。它不仅奠定了现代通信技术的基础，也对计算机科学、人工智能、生物学等众多领域产生了深远影响。香农在《通信的数学理论》一文中首次提出了信息熵的概念，为衡量信息量提供了一个精确的数学模型。随后，信息论的发展经历了从基础理论到广泛应用于实践的演变过程，覆盖了包括编码理论、数据压缩、错误控制等众多子领域。本章旨在简述信息论的历史起源，探索其在不同领域的应用以及对未来技术发展的影响。

# 2. 信息论中的基本概念与原理

## 2.1 信息的概念与度量
### 2.1.1 信息的定义
信息是数据和事实的一种表述形式，它可以是任何形式的、可以被传递的知识或消息。在信息论中，信息不仅仅指内容，更多的是指消息中的不确定性或意外性。这种度量的信息概念，让信息与知识和数据相区别，信息的价值在于它能够减少接收者的不确定性。例如，天气预报中关于“明天将下雨”的信息，比“明天有降水”的信息含有更多的确定性，因此传递了更多的信息。

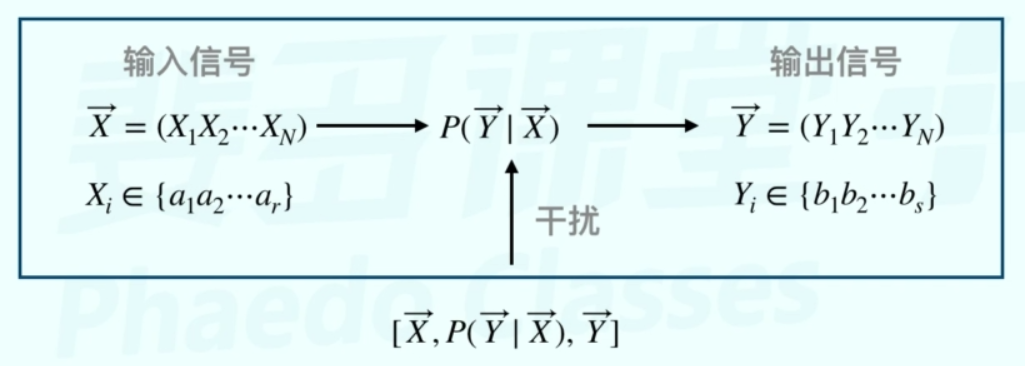
### 2.1.2 信息熵与互信息
信息熵是指一个信息系统的平均信息量，它衡量的是信息的不确定性程度。数学上，信息熵通常表示为H(X)，其中X是一个随机变量，表示可能的信息状态。信息熵的公式为：

H(X) = -Σp(x)logp(x)

这里，p(x)代表随机变量X取某一特定值x的概率，Σ表示对所有可能的x值求和。当所有可能的事件等可能时，信息熵达到最大。

互信息是衡量两个信息系统之间信息共通性的一个指标。如果两个系统之间的互信息高，表明一个系统的信息能够较多地预测另一个系统的信息。互信息的计算公式是：

I(X; Y) = ΣΣp(x, y)log(p(x, y)/(p(x)p(y)))

其中，I(X; Y)表示随机变量X和Y之间的互信息，p(x, y)是X和Y同时发生的概率。

## 2.2 信道容量与编码定理
### 2.2.1 信道容量的定义
信道容量是指在给定的传输媒介下，可以无误差传输的最大信息速率。香农第一定理指出，如果传输速率低于信道容量，那么存在一种编码方式可以任意小的错误概率传输信息。香农用信道容量C来定义这个最大传输速率：

C = Blog2(1 + S/N)

其中，B表示信道的带宽，S/N是信号与噪声的功率比。信道容量的概念为通信系统的设计提供了理论上的极限。

### 2.2.2 香农第一定理与编码策略
香农第一定理，又称噪声下的编码定理，解释了如何在有噪声的信道中有效传输信息。根据香农定理，通过使用适当的编码策略，可以实现信息以接近信道容量的速率进行传输，同时保持任意低的错误概率。这通常需要采用复杂度较高的编码算法，如前向纠错编码（FEC）。

### 2.2.3 信道编码与解码技术
信道编码技术是信息论和数字通信中的关键技术，它可以有效提高通信的可靠性，防止或减少噪声和干扰的影响。现代通信系统中常用的信道编码技术包括卷积编码、Turbo编码和低密度奇偶校验（LDPC）码等。这些编码技术能够允许接收端识别和纠正错误，从而提高数据传输的准确性。

## 2.3 无损与有损数据压缩
### 2.3.1 无损压缩算法
无损压缩是数据压缩的一种方式，它允许数据在压缩后能够完全无误差地恢复到原始状态。常见的无损压缩算法有Huffman编码、Lempel-Ziv-Welch (LZW)算法和算术编码等。Huffman编码的基本思想是为常见的字符分配较短的编码，为不常见的字符分配较长的编码，从而达到压缩数据的目的。

### 2.3.2 有损压缩原理与应用
有损压缩是在压缩过程中允许一定程度的数据丢失，以换取更高的压缩率。典型的有损压缩应用包括图像和音频文件的压缩。例如，JPEG图像压缩标准就采用有损压缩，它通过舍弃人眼不太能察觉的图像细节来减小文件大小。音频文件的MP3格式也是一种常见的有损压缩方法。

## 2.4 信息论中的信道编码和解码技术
信道编码和解码技术是通信系统中的核心组成部分，它们确保了数据在传输过程中的准确性和可靠性。以下代码块展示了如何使用Huffman编码算法进行无损压缩：

import heapq
from collections import defaultdict, Counter

# 创建一个优先队列，存放叶节点
def create_huffman_tree(node频率表):
    priority_queue = [weight for weight in node频率表]
    heapq.heapify(priority_queue)
    while len(priority_queue) > 1:
        lo = heapq.heappop(priority_queue)
        hi = heapq.heappop(priority_queue)
        for pair in lo[1:]:
            pair[1] = (pair[1], lo[0])
        for pair in hi[1:]:
            pair[1] = (pair[1], hi[0])
        heapq.heappush(priority_queue, lo + hi)
    return priority_queue[0]

# 构建Huffman树并生成编码
def huffman_encoding(data):
    node频率表 = Counter(data)
    huffman_tree = create_huffman_tree(node频率表)
    huffman_codes = {}
    def _huffman_codes(node, prefix=''):
        if isinstance(node, tuple):
            huffman_codes[node[0]] = prefix
            _huffman_codes(node[1][0], prefix + str(node[1][1]))
            _huffman_codes(node[2][0], prefix + str(node[2][1]))
        else:
            huffman_codes[node] = prefix
    _huffman_codes(huffman_tree)
    return huffman_codes

# 例如对字符串"mississippi"进行Huffman编码
data = "mississippi"
huffman_codes = huffman_encoding(data)
encoded_data = ''.join(huffman_codes[c] for c in data)
print("编码后的数据:", encoded_data)

上述代码段实现了一个基本的Huffman编码算法。首先，创建一个优先队列并按字符频率排序，然后逐步合并节点以构建Huffman树。每个字符都被赋予了一个唯一的二进制编码，频率高的字符拥有较短的编码。最后，使用这些编码对数据进行编码。解码过程可以通过遍历Huffman树反向追踪每个字符的路径来完成。

在下一章节，我们将深入探讨信息论在计算机科学中的应用，包括算法复杂度、信息安全、网络协议等方面的内容。

# 3. ```
# 第三章：信息论在计算机科学中的应用

随着计算机科学的发展，信息论在各个领域的应用越来越广泛。这一章节将深入探讨信息论在计算机科学中应用的多个方面，包括算法复杂度分析、信息安全与加密技术、以及数据通信与网络协议。

## 3.1 信息论与算法复杂度
在研究算法的效率时，信息论提供了一种独特的视角。它不仅帮助我们理解算法的复杂度，还指导我们优化算法以处理更多的数据。

### 3.1.1 算法复杂度的衡量
衡量一个算法是否高效，通常使用时间复杂度和空间复杂度两个标准。时间复杂度描述了算法执行时间随输入规模增长的变化趋势，而空间复杂度则描述了算法执行过程中占用存储空间的增长趋势。

**代码示例：**

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n