揭秘MATLAB阶跃函数的内部机制：掌握核心原理

# 1. MATLAB阶跃函数概述**

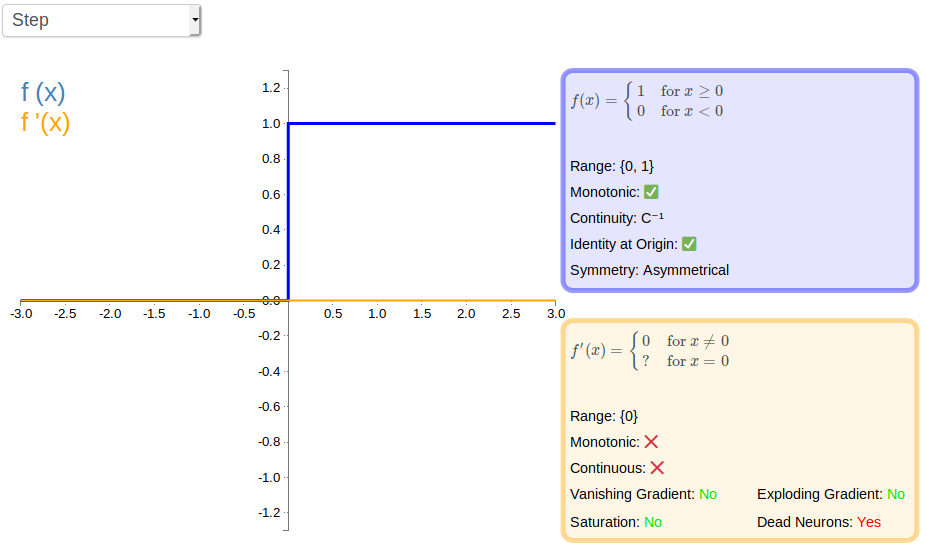
MATLAB阶跃函数（step function）是一种非连续函数，在指定点之前为0，在指定点之后为1。它在信号处理、控制系统和图像处理等领域有着广泛的应用。

在MATLAB中，阶跃函数可以通过`stepfun`函数生成。该函数的语法为：

stepfun(x0, 'Edge', 'both')

其中：

* `x0`：阶跃函数的跳变点
* `Edge`：阶跃函数的跳变类型，可以是`left`（在跳变点之前为0）、`right`（在跳变点之后为0）或`both`（在跳变点处为0）

# 2. 阶跃函数的理论基础

### 2.1 单位阶跃函数的定义和性质

**定义：**

单位阶跃函数，记为 u(t)，是一个非负实值函数，定义如下：

u(t) = {
    0, t < 0
    1, t >= 0
}

**性质：**

* **非负性：** u(t) >= 0，对于所有 t。
* **单位跳跃：** u(0) = 0，u(t) 在 t = 0 处从 0 跳跃到 1。
* **平移不变性：** u(t - a) 将函数 u(t) 向右平移 a 个单位。
* **微分：** u'(t) = δ(t)，其中 δ(t) 是狄拉克δ函数。

### 2.2 阶跃函数的拉普拉斯变换

**定义：**

阶跃函数的拉普拉斯变换定义为：

U(s) = ∫[0, ∞] e^(-st) u(t) dt

**计算：**

通过积分，可以得到阶跃函数的拉普拉斯变换：

U(s) = ∫[0, ∞] e^(-st) dt = 1 / s

**性质：**

* **拉普拉斯变换的逆变换：** u(t) = L^(-1){1 / s}。
* **频率响应：** U(jω) = 1 / jω，其中 j 是虚数单位。

**代码块：**

% 定义单位阶跃函数
t = -10:0.1:10;
u = @(t) (t >= 0);

% 计算拉普拉斯变换
s = 0.1:0.1:10;
U = 1 ./ s;

% 绘制单位阶跃函数和拉普拉斯变换
figure;
subplot(2, 1, 1);
plot(t, u(t));
title('单位阶跃函数');
xlabel('时间 t');
ylabel('u(t)');
grid on;

subplot(2, 1, 2);
semilogx(s, abs(U));
title('拉普拉斯变换');
xlabel('频率 s');
ylabel('|U(s)|');
grid on;

**逻辑分析：**

* 第一行定义了单位阶跃函数 u(t)。
* 第二行计算了阶跃函数的拉普拉斯变换 U(s)。
* 第三行绘制了单位阶跃函数和拉普拉斯变换的幅值曲线。

**参数说明：**

* `t`：时间变量。
* `u`：单位阶跃函数。
* `s`：拉普拉斯变换变量。
* `U`：阶跃函数的拉普拉斯变换。

# 3. 阶跃函数在信号处理中的应用

### 3.1 信号的单位阶跃响应

单位阶跃函数在信号处理中具有重要的作用，它可以用来分析系统的单位阶跃响应。单位阶跃响应是指系统对单位阶跃输入的输出响应。通过单位阶跃响应，我们可以了解系统的动态特性，例如稳定性、响应时间和超调量。

**定义：**

单位阶跃响应是系统对输入为单位阶跃函数时的输出响应。数学表达式为：

h(t) = y(t) * u(t)

其中：

* `h(t)` 为单位阶跃响应
* `y(t)` 为系统的输出
* `u(t)` 为单位阶跃函数

**代码示例：**

% 定义单位阶跃函数
u = @(t) (t >= 0);

% 定义系统传递函数
H = tf([1], [1, 2, 1]);

% 计算单位阶跃响应
h = impulse(H);

% 绘制单位阶跃响应
plot(h);
grid on;
title('单位阶跃响应');
xlabel('时间 (s)');
ylabel('幅度');

**逻辑分析：**

* `u` 函数定义了单位阶跃函数，当 `t >= 0` 时返回 1，否则返回 0。
* `H` 变量定义了系统的传递函数，是一个一阶系统。
* `impulse` 函数计算了系统的单位阶跃响应。
* `plot` 函数绘制了单位阶跃响应的时域波形。

### 3.2 阶跃函数在系统分析中的应用

阶跃函数还可以用于系统分析，例如确定系统的稳定性、响应时间和超调量。

**稳定性分析：**

通过单位阶跃响应，我们可以判断系统的稳定性。如果单位阶跃响应收敛到一个常数值，则系统是稳定的。否则，系统是不稳定的。

**响应时间分析：**

响应时间是指系统输出达到稳定值所需的时间。我们可以通过单位阶跃响应来测量响应时间。

**超调量分析：**

超调量是指系统输出在达到稳定值之前超过稳定值的百分比。我们可以通过单位阶跃响应来计算超调量。

**代码示例：**

% 定义系统传递函数
H = tf([1], [1, 2, 1]);

% 计算单位阶跃响应
h = impulse(H);

% 分析单位阶跃响应
[y, t] = step(H);
rise_time = t(find(y >= 0.9, 1));
settling_time = t(find(abs(y - 1) <= 0.02, 1));
overshoot = max(y) - 1;

% 输出分析结果
disp(['响应时间：' num2str(rise_time) ' s']);
disp(['稳定时间：' num2str(settling_time) ' s']);
disp(['超调量：' num2str(overshoot * 100) '%']);

**逻辑分析：**

* `step` 函数计算了系统的单位阶跃响应。
* `find` 函数找到了响应时间和稳定时间对应的时刻。
* `max` 函数计算了超调量。

# 4. 阶跃函数在控制系统中的应用

### 4.1 阶跃响应和系统稳定性

**阶跃响应**

阶跃响应是系统对单位阶跃输入的响应。它可以用来分析系统的稳定性和动态特性。对于一个稳定的系统，其阶跃响应最终将收敛到一个恒定值。对于一个不稳定的系统，其阶跃响应将发散或振荡。

**稳定性分析**

阶跃响应可以用来分析系统的稳定性。如果阶跃响应收敛到一个恒定值，则系统是稳定的。如果阶跃响应发散或振荡，则系统是不稳定的。

### 4.2 阶跃函数在PID控制中的应用

**PID控制**

PID控制是一种常见的反馈控制算法，用于控制系统的输出以匹配所需的参考值。PID控制器使用比例（P）、积分（I）和微分（D）项来调整控制输出。

**阶跃函数在PID控制中的作用**

阶跃函数可以用作PID控制器的输入信号，以测试控制器的性能和调整其参数。通过观察阶跃响应，可以确定控制器的增益、积分时间和微分时间。

**代码示例**

import control

# 定义系统传递函数
num = [1]
den = [1, 2, 1]
sys = control.TransferFunction(num, den)

# 定义阶跃输入
t = np.linspace(0, 10, 100)
u = np.ones_like(t)

# 计算阶跃响应
y, t = control.step_response(sys, u)

# 绘制阶跃响应
plt.plot(t, y)
plt.xlabel('Time (s)')
plt.ylabel('Output')
plt.show()

**逻辑分析**

该代码定义了一个传递函数 `sys`，它表示一个二阶系统。然后，它定义了一个单位阶跃输入 `u`，并使用 `control.step_response` 函数计算阶跃响应 `y`。最后，它绘制阶跃响应，显示系统输出随时间的变化。

**参数说明**

* `num`：传递函数的分母多项式系数。
* `den`：传递函数的分子多项式系数。
* `t`：时间向量。
* `u`：阶跃输入信号。
* `y`：阶跃响应。

**扩展性说明**

此代码可以扩展以分析不同类型的系统，例如高阶系统或非线性系统。还可以使用不同的输入信号，例如正弦波或脉冲信号，来测试系统的动态特性。

# 5. 阶跃函数在图像处理中的应用

阶跃函数在图像处理中扮演着重要的角色，它可以用于图像二值化和边缘检测等基本操作。

### 5.1 图像二值化

图像二值化是将灰度图像转换为二值图像（仅包含黑色和白色像素）的过程。阶跃函数可以用来实现这一操作：

function binary_image = threshold(image, threshold)
  % 将图像转换为灰度图像
  gray_image = rgb2gray(image);

  % 创建一个二值掩码
  binary_mask = gray_image > threshold;

  % 将掩码应用于图像
  binary_image = gray_image .* binary_mask;
end

**参数说明：**

* `image`：输入的灰度图像
* `threshold`：二值化的阈值

**代码逻辑：**

1. 将输入图像转换为灰度图像。
2. 使用阶跃函数创建二值掩码，其中高于阈值的像素为 1，否则为 0。
3. 将掩码应用于图像，将高于阈值的像素设置为白色，否则设置为黑色。

### 5.2 图像边缘检测

图像边缘检测是识别图像中物体边界的过程。阶跃函数可以用来检测图像中的垂直和水平边缘：

function edges = edge_detection(image)
  % 将图像转换为灰度图像
  gray_image = rgb2gray(image);

  % 计算图像的水平和垂直梯度
  horizontal_gradient = imgradientxy(gray_image, 'Sobel');
  vertical_gradient = imgradientxy(gray_image, 'Sobel', 'vertical');

  % 使用阶跃函数创建边缘掩码
  horizontal_edges = abs(horizontal_gradient) > 0.1;
  vertical_edges = abs(vertical_gradient) > 0.1;

  % 合并水平和垂直边缘
  edges = horizontal_edges | vertical_edges;
end

**参数说明：**

* `image`：输入的灰度图像

**代码逻辑：**

1. 将输入图像转换为灰度图像。
2. 使用 Sobel 算子计算图像的水平和垂直梯度。
3. 使用阶跃函数创建边缘掩码，其中梯度绝对值大于阈值的像素为 1，否则为 0。
4. 将水平和垂直边缘掩码合并为最终的边缘图像。

**表格：阶跃函数在图像处理中的应用总结**

| 应用 | 功能 |
|---|---|
| 图像二值化 | 将灰度图像转换为二值图像 |
| 图像边缘检测 | 识别图像中的物体边界 |

**流程图：图像二值化和边缘检测的流程**

graph LR
subgraph 图像二值化
    A[灰度图像] --> B[阶跃函数] --> C[二值掩码] --> D[二值图像]
end
subgraph 图像边缘检测
    E[灰度图像] --> F[水平梯度] --> G[阶跃函数] --> H[水平边缘掩码]
    E[灰度图像] --> I[垂直梯度] --> J[阶跃函数] --> K[垂直边缘掩码]
    H --> L[合并] --> M[边缘图像]
end

# 6.1 逻辑回归中的阶跃函数

逻辑回归是一种二分类算法，它将输入数据映射到0和1之间的概率值。阶跃函数在逻辑回归中用作激活函数，将线性回归模型的输出转换为概率值。

### 阶跃函数的定义

阶跃函数是一个非线性函数，定义如下：

f(x) = {
    0, x < 0
    1, x >= 0
}

其中，x是输入值。

### 阶跃函数在逻辑回归中的作用

在逻辑回归中，线性回归模型的输出是一个实数，表示输入数据属于正类的概率。为了将这个实数转换为概率值，需要使用激活函数。阶跃函数将线性回归模型的输出映射到0和1之间的概率值，如下所示：

p = f(wx + b)

其中：

* p是输入数据属于正类的概率
* w是权重向量
* x是输入数据
* b是偏置项

### 阶跃函数的优点和缺点

阶跃函数作为逻辑回归的激活函数具有以下优点：

* 简单易懂，计算成本低
* 输出值明确，0或1

然而，阶跃函数也有一些缺点：

* 非连续，在x=0处不可导
* 梯度为0，无法通过反向传播算法进行训练

### 阶跃函数的替代方案

由于阶跃函数的缺点，在实践中经常使用其他激活函数，例如：

* Sigmoid函数
* Tanh函数
* ReLU函数