揭秘MATLAB求矩阵秩的奥秘：从理论到实践的全面解读

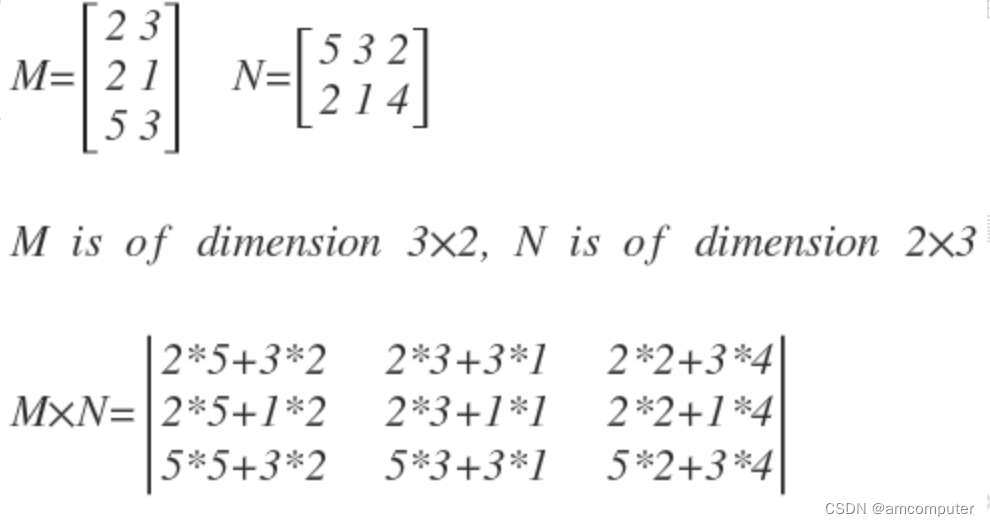
# 1. 矩阵秩的理论基础**

矩阵秩是衡量矩阵线性相关性的一个重要指标，反映了矩阵中线性无关行（或列）的个数。对于一个m×n矩阵A，其秩r定义为：

- A中线性无关行（或列）的最大个数
- A的非零行阶梯形的行数
- A的非零特征值的个数

矩阵秩具有以下性质：

- r(A) ≤ min(m, n)
- r(A) = r(A^T)
- r(AB) ≤ min(r(A), r(B))

# 2. MATLAB中求矩阵秩的实践方法

### 2.1 rank()函数的基本用法

**功能描述：**

`rank()`函数用于计算矩阵的秩。它返回一个标量，表示矩阵的秩。

**语法：**

r = rank(A)

**参数说明：**

* `A`：要计算秩的矩阵。

**代码示例：**

A = [1 2 3; 4 5 6; 7 8 9];
r = rank(A)

**逻辑分析：**

该代码示例创建一个3x3矩阵`A`，然后使用`rank()`函数计算其秩。结果存储在变量`r`中。

### 2.2 rref()函数的应用

**功能描述：**

`rref()`函数将矩阵化为行阶梯形，并返回一个等价的行阶梯形矩阵。矩阵的秩等于行阶梯形矩阵中的非零行的数量。

**语法：**

R = rref(A)

**参数说明：**

* `A`：要化为行阶梯形的矩阵。

**代码示例：**

A = [1 2 3; 4 5 6; 7 8 9];
R = rref(A)

**逻辑分析：**

该代码示例创建一个3x3矩阵`A`，然后使用`rref()`函数将其化为行阶梯形。结果存储在变量`R`中。

### 2.3 cond()函数的辅助作用

**功能描述：**

`cond()`函数计算矩阵的条件数，它衡量矩阵对扰动的敏感性。条件数较大的矩阵被称为病态矩阵，求解其秩时可能存在数值误差。

**语法：**

c = cond(A)

**参数说明：**

* `A`：要计算条件数的矩阵。

**代码示例：**

A = [1 2 3; 4 5 6; 7 8 9];
c = cond(A)

**逻辑分析：**

该代码示例创建一个3x3矩阵`A`，然后使用`cond()`函数计算其条件数。结果存储在变量`c`中。

# 3.1 线性方程组的求解

矩阵秩在求解线性方程组中扮演着至关重要的角色。线性方程组可以表示为：

Ax = b

其中，A 是系数矩阵，x 是未知数向量，b 是常数向量。

矩阵秩可以帮助我们判断线性方程组是否有解，以及解的个数。具体来说：

- **如果 A 的秩等于未知数的个数（即列数），则方程组有唯一解。**
- **如果 A 的秩小于未知数的个数，则方程组无解。**
- **如果 A 的秩大于未知数的个数，则方程组有无穷多个解。**

**例：**

考虑以下线性方程组：

[2 1] [x1]   [3]
[4 2] [x2] = [6]

系数矩阵 A 的秩为 2，等于未知数的个数。因此，该方程组有唯一解。

**代码块：**

% 系数矩阵 A
A = [2 1; 4 2];

% 常数向量 b
b = [3; 6];

% 求矩阵 A 的秩
rank_A = rank(A);

% 判断方程组的解
if rank_A == size(A, 2)
    disp('方程组有唯一解。');
else
    disp('方程组无解。');
end

**逻辑分析：**

该代码块首先定义了系数矩阵 A 和常数向量 b。然后，使用 rank() 函数计算矩阵 A 的秩。最后，根据矩阵 A 的秩判断方程组的解是否存在。

**参数说明：**

- `A`：系数矩阵
- `b`：常数向量
- `rank_A`：矩阵 A 的秩

**扩展性说明：**

矩阵秩在求解线性方程组中的应用非常广泛。例如，在物理学中，矩阵秩可以用来求解电路中的电流和电压；在经济学中，矩阵秩可以用来求解投入产出模型。

# 4. MATLAB中矩阵秩的进阶应用

### 4.1 奇异值分解（SVD）

#### 4.1.1 SVD的原理和计算方法

奇异值分解（SVD）是一种将矩阵分解为三个矩阵的数学技术：一个正交矩阵U、一个对角矩阵Σ和一个正交矩阵V。其分解形式为：

A = UΣV^T

其中：

* A 是原始矩阵
* U 是左奇异向量矩阵，其列向量是 A 的左奇异向量
* Σ 是奇异值矩阵，其对角线元素是 A 的奇异值
* V 是右奇异向量矩阵，其列向量是 A 的右奇异向量

奇异值是 A 的特征值的平方根，表示 A 的线性变换的伸缩因子。奇异值矩阵 Σ 的秩等于 A 的秩。

在 MATLAB 中，可以使用 `svd()` 函数进行 SVD 分解。语法如下：

[U, S, V] = svd(A)

其中：

* U 是左奇异向量矩阵
* S 是奇异值矩阵
* V 是右奇异向量矩阵

#### 4.1.2 SVD在图像处理中的应用

SVD 在图像处理中有着广泛的应用，例如图像降噪、图像压缩和图像增强。

* **图像降噪：**SVD 可以将图像分解为奇异值、奇异向量和噪声分量。通过去除噪声分量，可以有效地降低图像噪声。
* **图像压缩：**SVD 可以将图像表示为一组奇异值和奇异向量的线性组合。通过截断较小的奇异值，可以实现图像压缩。
* **图像增强：**SVD 可以用于图像锐化、对比度增强和颜色校正。通过调整奇异值和奇异向量的权重，可以增强图像的特定特征。

### 4.2 QR分解

#### 4.2.1 QR分解的原理和算法

QR分解是一种将矩阵分解为一个正交矩阵Q和一个上三角矩阵R的数学技术。其分解形式为：

A = QR

其中：

* A 是原始矩阵
* Q 是正交矩阵，其列向量是 A 的正交基
* R 是上三角矩阵

QR分解可以使用 Gram-Schmidt 正交化算法计算。该算法的步骤如下：

1. 将 A 的第一列归一化，得到 Q 的第一列 q1。
2. 将 A 的第二列减去 q1 的投影，得到 A 的第二列的正交分量。将该分量归一化，得到 Q 的第二列 q2。
3. 重复步骤 2，直到 A 的所有列都正交化。
4. 将正交化的列向量组成 Q，将 A 减去 Q 的投影得到 R。

#### 4.2.2 QR分解在求解线性最小二乘问题中的应用

QR分解在求解线性最小二乘问题中有着重要的应用。线性最小二乘问题可以表示为：

min ||Ax - b||^2

其中：

* A 是 m×n 矩阵
* x 是 n×1 向量
* b 是 m×1 向量

使用 QR 分解，可以将该问题转化为：

min ||Rx - Q^Tb||^2

由于 R 是上三角矩阵，因此该问题可以高效地使用回代法求解。

# 5. 矩阵秩的优化计算

### 5.1 稀疏矩阵的秩计算

对于稀疏矩阵，即元素中大部分为零的矩阵，其秩的计算可以采用专门针对稀疏矩阵的算法，以提高计算效率。MATLAB中提供了`sprank()`函数，专门用于计算稀疏矩阵的秩。

% 创建一个稀疏矩阵
A = sparse([1, 2, 3; 4, 5, 6; 7, 8, 9]);

% 计算稀疏矩阵的秩
rank_A = sprank(A);

% 输出结果
disp(['稀疏矩阵的秩为：' num2str(rank_A)]);

**代码逻辑分析：**

* `sprank(A)`函数计算稀疏矩阵`A`的秩，并返回秩的值。
* `disp()`函数输出计算结果。

### 5.2 大规模矩阵的秩近似计算

对于大规模矩阵，直接计算其秩可能非常耗时。此时，可以采用秩近似的方法，通过计算矩阵的奇异值分解（SVD）来近似其秩。

% 创建一个大规模矩阵
n = 1000;  % 矩阵大小
A = randn(n);

% 计算矩阵的奇异值分解
[U, S, V] = svd(A);

% 奇异值阈值
threshold = 1e-6;

% 计算秩近似值
rank_approx = sum(diag(S) > threshold);

% 输出结果
disp(['大规模矩阵的秩近似值为：' num2str(rank_approx)]);

**代码逻辑分析：**

* `randn(n)`函数生成一个`n`阶随机矩阵。
* `svd(A)`函数计算矩阵`A`的奇异值分解，返回奇异值矩阵`U`、`S`和`V`。
* `diag(S)`函数提取奇异值矩阵`S`的对角线元素。
* `sum(diag(S) > threshold)`计算大于给定阈值`threshold`的奇异值的个数，即秩近似值。
* `disp()`函数输出计算结果。

**参数说明：**

* `threshold`：奇异值阈值，用于确定秩近似值。

# 6. MATLAB求矩阵秩的常见问题与解决方法**

### 6.1 数值误差的影响

在MATLAB中求矩阵秩时，由于浮点运算的误差，可能会导致秩计算结果与理论值略有偏差。尤其是对于接近奇异的矩阵，数值误差的影响会更加明显。

为了减小数值误差的影响，可以采用以下方法：

- 使用高精度的浮点数据类型，如`double`或`long double`。
- 使用数值稳定的算法，如SVD或QR分解。
- 对计算结果进行容差判断，避免误差导致错误的结论。

### 6.2 病态矩阵的处理

病态矩阵是指条件数很大的矩阵。对于病态矩阵，即使很小的扰动也会导致秩计算结果发生较大的变化。

处理病态矩阵时，可以采用以下方法：

- 使用稳定性较好的算法，如SVD或QR分解。
- 对矩阵进行正则化处理，减小其条件数。
- 降低秩计算的精度要求，避免过分追求精确性。

### 6.3 矩阵秩计算的效率优化

对于大规模矩阵，直接计算秩可能会非常耗时。为了提高效率，可以采用以下优化方法：

- 使用稀疏矩阵存储技术，减少内存占用和计算量。
- 采用分块计算策略，将大矩阵分解为多个小块，分而治之。
- 利用并行计算技术，充分利用多核处理器的优势。

% 优化矩阵秩计算的示例代码
A = randn(1000, 1000);  % 生成一个大规模随机矩阵
A_sparse = sparse(A);  % 将矩阵转换为稀疏矩阵

% 使用SVD计算秩
[U, S, V] = svd(A_sparse);
rank_A = sum(S > 1e-10);  % 设定阈值判断秩

% 使用并行计算加速秩计算
parfor i = 1:size(A, 1)
    rank_A_i = rank(A(i, :));  % 计算每一行的秩
end
rank_A_parallel = max(rank_A_i);  % 取最大秩作为矩阵秩