MATLAB余数与数值方法：揭示余数在数值计算中的重要性

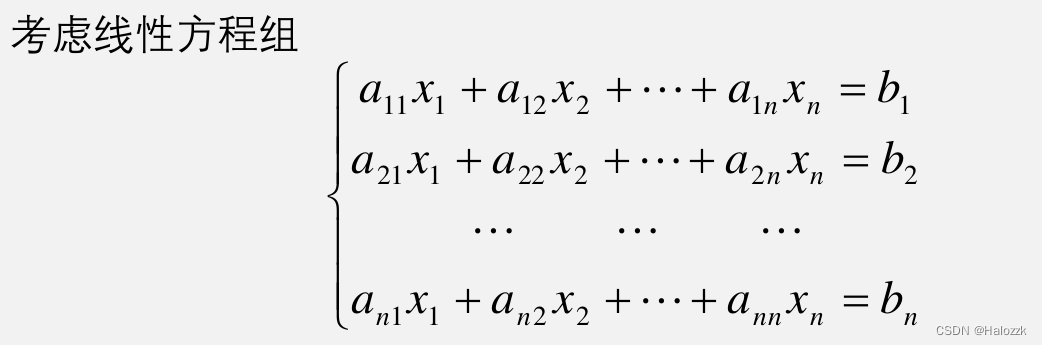
# 1. MATLAB中的余数运算**

**1.1 余数运算符**

MATLAB中使用`mod`运算符进行余数运算。该运算符接受两个参数：被除数和除数。余数是除法运算中除不尽的部分。例如：

mod(10, 3) % 结果为 1

**1.2 余数运算的性质**

余数运算具有以下性质：

* 余数的符号与被除数的符号相同。
* 余数的绝对值小于除数的绝对值。
* 对于任何整数`a`和`b`，`mod(a, b)`等于`a - b * floor(a/b)`。

# 2. 余数在数值方法中的应用

余数运算在数值方法中有着广泛的应用，特别是在伪随机数生成、数值积分和数值求解等领域。

### 2.1 模运算在伪随机数生成中的应用

伪随机数生成是数值方法中一项重要的任务，它为模拟和建模提供了随机性。余数运算在伪随机数生成中扮演着至关重要的角色。

#### 2.1.1 线性同余法

线性同余法是一种经典的伪随机数生成方法，其公式为：

x_n = (a * x_{n-1} + c) mod m

其中：

* `x_n` 是第 `n` 个伪随机数
* `x_{n-1}` 是第 `n-1` 个伪随机数
* `a` 是乘法常数
* `c` 是加法常数
* `m` 是模数

线性同余法的伪随机性取决于参数 `a`、`c` 和 `m` 的选择。

#### 2.1.2 梅森旋转法

梅森旋转法是一种改进的线性同余法，其公式为：

x_n = (x_{n-1} >> r) ^ (x_{n-1} & (2^r - 1))

其中：

* `x_n` 是第 `n` 个伪随机数
* `x_{n-1}` 是第 `n-1` 个伪随机数
* `r` 是旋转位数

梅森旋转法具有更长的周期和更好的随机性，广泛用于各种应用中。

### 2.2 余数在数值积分中的应用

数值积分是求解积分的近似值，它在科学计算和工程应用中有着广泛的应用。余数运算在数值积分中也发挥着重要作用。

#### 2.2.1 蒙特卡洛积分法

蒙特卡洛积分法是一种基于随机抽样的数值积分方法。其基本思想是在积分域内随机生成样本点，并根据样本点的数量和函数值来估计积分值。

蒙特卡洛积分法中，余数运算用于生成随机数。通过对随机数取模，可以将随机数映射到积分域内。

#### 2.2.2 准蒙特卡洛积分法

准蒙特卡洛积分法是蒙特卡洛积分法的改进方法，它通过使用低差异序列来提高积分精度。低差异序列是一种具有均匀分布的伪随机数序列。

准蒙特卡洛积分法中，余数运算用于生成低差异序列。通过对伪随机数取模，可以得到具有均匀分布的低差异序列。

# 3.1 余数在求解线性方程组中的应用

#### 3.1.1 高斯消去法

高斯消去法是一种求解线性方程组的经典方法，它利用余数运算来消去方程组中的变量。

**步骤：**

1. 将方程组转换为增广矩阵形式。
2. 对增广矩阵进行行变换，将主对角线上的元素化为 1，其他元素化为 0。
3. 从上到下依次求解变量。

**代码块：**

% 定义增广矩阵
A = [2 1 1; 4 3 2; 8 7 4];
b = [4; 10; 20];

% 进行高斯消去
for i = 1:size(A, 1)
    % 将主对角线元素化为 1
    A(i, :) = A(i, :) / A(i, i);
    % 消去其他行中的主对角线元素
    for j = i+1:size(A, 1)
        A(j, :) = A(j, :) - A(j, i) * A(i, :);
    end
end

% 求解变量
x = A(:, end) ./ A(:, 1:end-1);

% 输出结果
disp(x);

**逻辑分析：**

* 第一个循环将主对角线元素化为 1。
* 第二个循环消去其他行中的主对角线元素。
* 最后的计算求解了变量。

#### 3.1.2 LU分解法

LU分解法是一种将矩阵分解为下三角矩阵和上三角矩阵的算法，它也可以用于求解线性方程组。

**步骤：**

1. 将矩阵分解为 LU 形式。
2. 求解 Ly = b。
3. 求解 Ux = y。

**代码块：**

% 定义矩阵
A = [2 1 1; 4 3 2; 8 7 4];
b = [4; 10; 20];

% LU 分解
[L, U] = lu(A);

% 求解 Ly = b
y = L \ b;

% 求解 Ux = y
x = U \ y;

% 输出结果
disp(x);

**逻辑分析：**

* `lu` 函数将矩阵分解为 LU 形式。
* `\` 运算符求解线性方程组。
* 最后的计算求解了变量。

### 3.2 余数在求解非线性方程组中的应用

#### 3.2.1 牛顿法

牛顿法是一种求解非线性方程组的迭代方法，它利用余数运算来计算方程组的根。

**步骤：**

1. 给定初始猜测值。
2. 计算方程组的雅可比矩阵。
3. 求解线性方程组 J(x) * dx = -f(x)。
4. 更新猜测值 x = x + dx。
5. 重复步骤 2-4，直到满足收敛条件。

**代码块：**

% 定义方程组
f = @(x) [x(1)^2 + x(2)^2 - 1; x(1) - x(2)];

% 给定初始猜测值
x0 = [0; 0];

% 迭代求解
for i = 1:100
    % 计算雅可比矩阵
    J = [2*x0(1), 2*x0(2); 1, -1];
    % 求解线性方程组
    dx = J \ (-f(x0));
    % 更新猜测值
    x0 = x0 + dx;
    % 检查收敛条件
    if norm(dx) < 1e-6
        break;
    end
end

% 输出结果
disp(x0);

**逻辑分析：**

* `f` 函数定义了方程组。
* `x0` 是初始猜测值。
* 循环迭代求解方程组。
* `J` 是雅可比矩阵。
* `\` 运算符求解线性方程组。
* `norm` 函数计算向量的范数，用于检查收敛条件。

#### 3.2.2 拟牛顿法

拟牛顿法是一种改进的牛顿法，它利用余数运算来近似雅可比矩阵，从而提高求解效率。

**步骤：**

1. 给定初始猜测值。
2. 计算方程组的梯度。
3. 近似雅可比矩阵。
4. 求解线性方程组 H(x) * dx = -f(x)。
5. 更新猜测值 x = x + dx。
6. 重复步骤 2-5，直到满足收敛条件。

**代码块