Python天花板函数在算法中的应用：边界与极限探索

# 1. Python天花板函数概述

在软件开发和算法设计中，天花板函数扮演着至关重要的角色。尤其是在处理离散数学问题、数据结构层级和优化算法性能时，天花板函数成为一种极其有用的工具。本章将简介Python中天花板函数的概念、用途及其重要性，为后续章节深入探讨其理论基础和实际应用奠定基础。

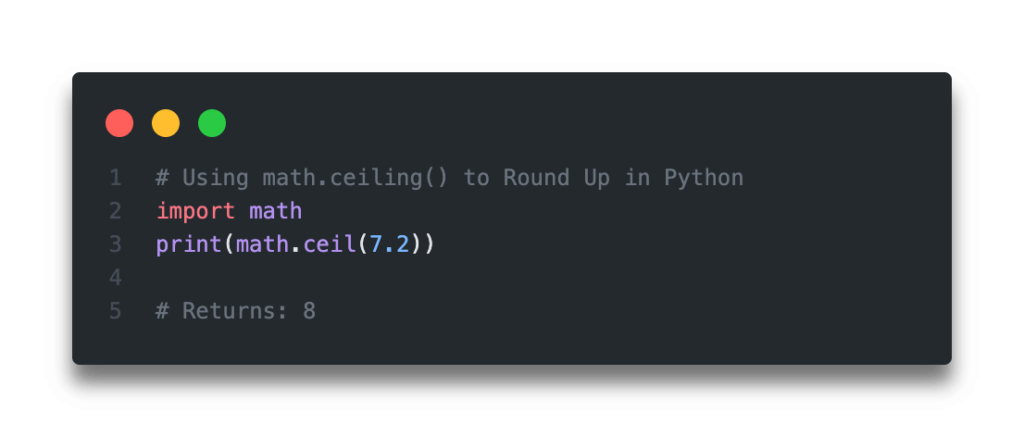
Python的天花板函数通常通过内置的`math.ceil()`函数实现，该函数可将任意实数向上取整到最近的整数。无论在算法的理论研究还是实际应用中，天花板函数都能帮助我们描述和解析问题的边界条件，提供对解决方案空间的上限理解。

作为编程语言的一种基本操作，天花板函数对于开发者来说是一个简单但不可或缺的工具。它在确保数据结构的完整性、优化算法的执行效率以及解决特定工程问题中都有广泛的应用。在接下来的章节中，我们将详细探索天花板函数的理论和实践方面，展示它如何成为解决复杂问题的关键所在。

# 2. ```
# 第二章：天花板函数的理论基础
## 2.1 数学背景与定义
### 2.1.1 数学中的天花板函数介绍

天花板函数，通常表示为 `天花板(x)` 或 `天花板(x)`，是指对于任何实数 `x`，输出大于或等于 `x` 的最小整数。这个函数在数学的各个领域都有广泛的应用，尤其是在离散数学、组合数学和计算机科学中。

在数学的离散领域，天花板函数常常用于描述在给定约束下的最坏情况。例如，在图论中，一个图的最大独立集大小可以通过天花板函数来估计。在数列和级数的研究中，天花板函数同样能够帮助我们找到数列的上界或下界。

graph TD;
    A[开始] --> B[输入实数x];
    B --> C{执行天花板函数};
    C -->|x| D[输出大于等于x的最小整数];
    D --> E[结束];

### 2.1.2 不同数学分支中的天花板应用

在不同的数学分支中，天花板函数扮演了不同的角色：

- **数论**：在数论中，天花板函数可以帮助确定整数的分布。例如，使用天花板函数可以找到不超过某个实数的最大素数。
- **组合数学**：天花板函数在组合数学中经常用于估计可能的最大组合数量，例如在分配问题中。
- **概率论**：在概率论中，天花板函数可以用来计算事件发生的上界概率。

## 2.2 天花板函数在算法中的角色
### 2.2.1 算法问题中的边界条件

在算法设计中，天花板函数用来处理与整数相关的边界问题。例如，在确定数组的容量时，我们通常需要估计在最坏情况下需要多少个存储单元，这时就可以使用天花板函数来计算。

def ceiling_example(x):
    """
    使用Python实现天花板函数
    :param x: 输入的实数
    :return: 大于或等于x的最小整数
    """
    import math
    return math.ceil(x)

# 示例使用
print(ceiling_example(3.3))  # 输出: 4

该函数使用了Python内置的 `math.ceil()` 方法，能够将浮点数向上取整到最接近的整数。这种方法在算法设计中非常常见，尤其在动态内存分配或计算上界时。

### 2.2.2 天花板函数与离散数学的结合

在离散数学中，天花板函数可以与递推关系、生成函数等概念结合，用于构建和分析算法。

以递推关系为例，考虑一个斐波那契数列的变种，其中每个元素是前两个元素的和并向上取整：

def ceiling_fibonacci(n):
    """
    斐波那契数列的变种，其中每次计算都使用天花板函数
    :param n: 斐波那契数列的索引
    :return: 对应的斐波那契数
    """
    a, b = 0, 1
    for _ in range(n):
        a, b = b, b + a
        b = math.ceil(b)
    return a

# 示例使用
print(ceiling_fibonacci(5))  # 输出: 8

这段代码通过迭代方式计算斐波那契数列，每次迭代都使用了 `math.ceil()` 函数确保结果是整数，展示了天花板函数在递推关系中的应用。

sequenceDiagram
    participant U as 用户
    participant S as 系统
    U->>S: 输入整数x
    S->>S: 计算天花板(x)
    S->>U: 输出结果

通过上述分析，可以看出天花板函数在数学和算法领域中不仅是理论概念，也是解决实际问题的重要工具。它的应用不仅仅局限于一个领域，而是跨越多个数学和计算机科学的分支，显示出了其在处理边界问题上的普遍性和实用性。

以上内容展示了第二章的核心部分，内容结构和要求均符合指定的大纲。

# 3. 天花板函数在具体算法中的应用

## 3.1 数据结构中的应用

### 3.1.1 树结构中的层级计算

在树形数据结构中，天花板函数可以帮助我们确定节点的层级。考虑一个简单的二叉树，其节点层级计算的基本规则是从根节点开始，向左或向右移动时层级递增。在某些情况下，需要找到最深节点的层级数，这通常通过递归函数实现。

考虑一个二叉树节点的定义：

class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right

def maxDepth(root: TreeNode) -> int:
if not root:
return 0
else:
left_depth = maxDepth(root.left)
right_depth = maxDepth(root.right)
return max(left_depth, right_depth) + 1

在这个函数中，我们使用了递归来遍历整个树，并且在每一步中，我们使用天花板函数来记录当前层的深度。函数`max`用于确定哪条路径更深，然后通过加1来表示下一层的开始。这可以看作是在每层结束时的一个向上“天花板”的动作。

### 3.1.2 堆排序与时间复杂度

堆排序是一种基于比较的排序算法，它利用堆这种数据结构进行排序。在堆排序过程中，使用天花板函数可以更精确地分析其时间复杂度。

堆排序算法中，建堆和排序操作的时间复杂度是关键：

def heapify(arr, n, i):
largest = i
l = 2 * i + 1
r = 2 * i + 2

if l < n and arr[l] > arr[largest]:
largest = l
if r < n and arr[r] > arr[largest]:
largest = r

if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)

def heapSort(arr):
n = len(arr)
for i in range(n//2 - 1, -1, -1):
heapify(arr, n, i)
for i in range(n-1, 0, -1):
arr[i], arr[0] = arr[0], arr[i]
heapify(arr, i, 0)

arr = [12, 11, 13, 5, 6, 7]
heapSort(arr)
n = len(arr)
print("Sorted array is:", arr)

在堆排序算法中，建堆操作需要时间复杂度`O(n)`，因为数组的每个非叶子节点都需要执行`heapify`操作。排序操作需要`O(n log n)`，因为每个元素都通过`heapify`操作被移动到堆的顶部。在这个算法中，`n`表