揭秘单片机温度控制核心算法：PID算法的深入解析

# 1. PID算法概述

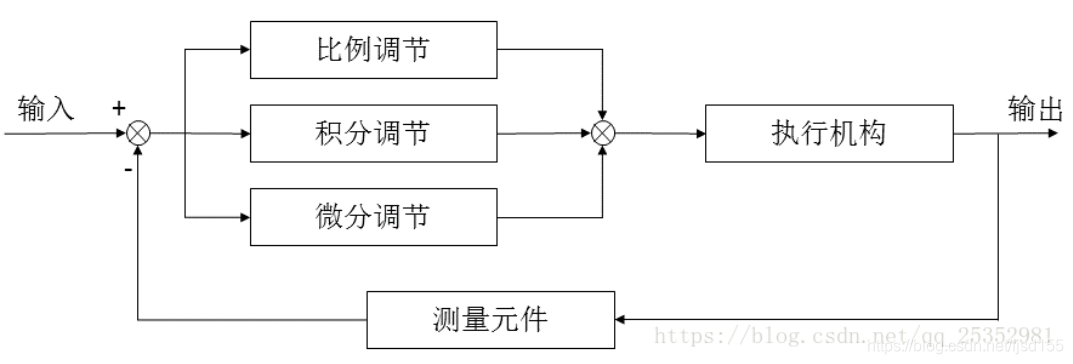
PID（比例-积分-微分）算法是一种经典的反馈控制算法，广泛应用于工业自动化、机器人控制等领域。其基本原理是通过测量被控对象（如温度、位置）的当前值与期望值之间的偏差，并根据偏差的大小和变化率，实时调整控制输出，以使被控对象达到期望状态。

PID算法的优点包括：结构简单、易于实现、鲁棒性强。其缺点是：参数整定较为复杂，需要根据被控对象的特性进行调整。

# 2. PID算法的理论基础

### 2.1 比例积分微分控制原理

PID算法是一种反馈控制算法，它通过测量被控对象的输出值与期望值之间的误差，并根据误差的比例、积分和微分值来计算控制量，从而实现对被控对象的控制。

**比例控制**：比例控制仅根据误差的当前值进行控制，控制量与误差成正比。比例控制的优点是响应快，但如果比例系数过大，容易引起系统振荡。

**积分控制**：积分控制根据误差的累积值进行控制，控制量与误差的积分值成正比。积分控制的优点是能消除稳态误差，但如果积分时间过长，容易引起系统超调。

**微分控制**：微分控制根据误差的变化率进行控制，控制量与误差的变化率成正比。微分控制的优点是能提高系统的稳定性，但如果微分时间过长，容易引起系统噪声放大。

### 2.2 PID算法的数学模型

PID算法的数学模型为：

u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt

其中：

* `u(t)`：控制量
* `e(t)`：误差
* `Kp`：比例系数
* `Ki`：积分系数
* `Kd`：微分系数

**参数说明**：

* `Kp`：比例系数，表示误差对控制量的比例放大倍数。
* `Ki`：积分系数，表示误差累积值对控制量的放大倍数。
* `Kd`：微分系数，表示误差变化率对控制量的放大倍数。

**逻辑分析**：

PID算法通过对误差的比例、积分和微分进行加权求和，得到控制量。比例控制能快速响应误差，积分控制能消除稳态误差，微分控制能提高系统稳定性。通过调整PID参数，可以优化控制效果。

**代码示例**：

import numpy as np

def pid_control(error, Kp, Ki, Kd, dt):
    """
    PID控制算法

    Args:
        error (float): 误差
        Kp (float): 比例系数
        Ki (float): 积分系数
        Kd (float): 微分系数
        dt (float): 采样时间

    Returns:
        float: 控制量
    """

    integral = 0
    derivative = 0

    integral += error * dt
    derivative = (error - prev_error) / dt

    control = Kp * error + Ki * integral + Kd * derivative

    return control

# 3.1 PID参数的整定方法

PID算法的性能在很大程度上取决于其参数的整定。参数整定是指根据被控对象和控制要求确定合适的PID参数。常用的PID参数整定方法包括：

#### 齐格勒-尼科尔斯法

齐格勒-尼科尔斯法是一种基于阶跃响应的整定方法。其步骤如下：

1. 将PID控制器切换到P控制模式，即设置积分项和微分项为0。
2. 施加阶跃输入信号，并记录被控对象的输出响应。
3. 确定响应曲线上的拐点时间`Tu`和峰值时间`Tp`。
4. 根据`Tu`和`Tp`计算PID参数：
- 比例增益：`Kp = 1.2 * (Tu / Tp)`
- 积分时间：`Ti = 2 * Tu`
- 微分时间：`Td = 0.5 * Tu`

#### 科恩-库恩法

科恩-库恩法也是一种基于阶跃响应的整定方法，但它考虑了被控对象的阻尼比。其步骤如下：

1. 施加阶跃输入信号，并记录被控对象的输出响应。
2. 确定响应曲线上上升到63.2%峰值所需的时间`tr`。
3. 根据`tr`计算PID参数：
- 比例增益：`Kp = (1.2 * π) / tr`
- 积分时间：`Ti = 2 * tr`
- 微分时间：`Td = 0.5 * tr`

#### 经验法

经验法是一种基于经验和试错的整定方法。其步骤如下：

1. 设置初始PID参数值，例如`Kp = 1`、`Ti = 1`、`Td = 0`。
2. 施加输入信号，并观察被控对象的响应。
3. 根据响应情况调整PID参数。例如，如果响应过冲，则减小`Kp`；如果响应太慢，则增大`Ti`。

#### 自适应整定法

自适应整定法是一种动态调整PID参数的方法。它利用被控对象的实时响应信息来更新PID参数。自适应整定法可以提高PID算法的鲁棒性和性能。

#### 3.2 PID算法在温度控制中的实现

PID算法广泛应用于温度控制系统。以下是一个使用PID算法实现温度控制的示例代码：

import time

# PID参数
Kp = 1.0
Ti = 1.0
Td = 0.0

# 温度传感器读取函数
def read_temperature():
    # 模拟读取温度传感器
    return 25.0

# 执行器控制函数
def control_actuator(output):
    # 模拟控制执行器
    print("执行器输出：", output)

# PID算法实现
def pid_control(setpoint, measurement):
    # 计算误差
    error = setpoint - measurement

    # 计算积分项
    integral = 0.0
    integral += error * Ti

    # 计算微分项
    derivative = 0.0
    if time.time() - last_time > Td:
        derivative = (error - last_error) / Td
        last_error = error
        last_time = time.time()

    # 计算PID输出
    output = Kp * error + integral + derivative

    # 限制输出范围
    output = min(max(output, 0.0), 100.0)

    return output

# 设置温度设定值
setpoint = 30.0

# 初始化时间
last_time = time.time()

# 主循环
while True:
    # 读取温度
    measurement = read_temperature()

    # 执行PID控制
    output = pid_control(setpoint, measurement)

    # 控制执行器
    control_actuator(output)

    # 等待一段时间
    time.sleep(0.1)

**代码逻辑分析：**

该代码实现了PID算法的温度控制。它首先读取温度传感器，然后根据PID算法计算PID输出。PID输出用于控制执行器，从而调节温度。

**参数说明：**

- `Kp`：比例增益
- `Ti`：积分时间
- `Td`：微分时间
- `setpoint`：温度设定值
- `measurement`：温度测量值
- `output`：PID输出

# 4. PID算法的优化策略

### 4.1 自适应PID算法

**原理**

自适应PID算法是一种能够根据被控对象的动态特性自动调整PID参数的算法。它通过实时监测被控对象的响应，并根据响应情况调整PID参数，以达到最佳控制效果。

**实现**

自适应PID算法的实现方法有多种，常用的方法包括：

- **基于模型的自适应PID算法：**该方法利用被控对象的数学模型来估计其动态特性，并根据估计结果调整PID参数。
- **基于观测器的自适应PID算法：**该方法利用观测器来估计被控对象的内部状态，并根据估计结果调整PID参数。
- **基于神经网络的自适应PID算法：**该方法利用神经网络来学习被控对象的动态特性，并根据学习结果调整PID参数。

**优点**

- 能够自动调整PID参数，适应被控对象的动态特性变化。
- 提高控制精度和鲁棒性。
- 简化PID参数整定过程。

**缺点**

- 算法复杂度较高，需要较多的计算资源。
- 对被控对象的数学模型或动态特性要求较高。

### 4.2 模糊PID算法

**原理**

模糊PID算法是一种将模糊逻辑应用于PID算法的算法。它通过将被控对象的输入、输出和PID参数表示为模糊变量，并利用模糊规则来调整PID参数，以达到最佳控制效果。

**实现**

模糊PID算法的实现步骤如下：

1. 将被控对象的输入、输出和PID参数表示为模糊变量。
2. 定义模糊规则，描述如何根据模糊变量调整PID参数。
3. 根据模糊规则和模糊推理，计算新的PID参数。

**优点**

- 能够处理非线性、不确定和模糊的被控对象。
- 提高控制精度和鲁棒性。
- 简化PID参数整定过程。

**缺点**

- 算法复杂度较高，需要较多的计算资源。
- 对模糊规则的定义要求较高。

**代码示例**

import numpy as np
import skfuzzy as fuzz

# 定义模糊变量
error = fuzz.linguistic_variable('error', np.arange(-10, 10, 0.1))
error_rate = fuzz.linguistic_variable('error_rate', np.arange(-10, 10, 0.1))
Kp = fuzz.linguistic_variable('Kp', np.arange(0, 10, 0.1))
Ki = fuzz.linguistic_variable('Ki', np.arange(0, 10, 0.1))
Kd = fuzz.linguistic_variable('Kd', np.arange(0, 10, 0.1))

# 定义模糊集
error_sets = {'NB': fuzz.trimf(error, [-10, -10, -5]),
              'NM': fuzz.trimf(error, [-10, -5, 0]),
              'NS': fuzz.trimf(error, [-5, 0, 5]),
              'ZE': fuzz.trimf(error, [0, 0, 0]),
              'PS': fuzz.trimf(error, [0, 5, 10]),
              'PM': fuzz.trimf(error, [5, 10, 10])}

error_rate_sets = {'NB': fuzz.trimf(error_rate, [-10, -10, -5]),
                  'NM': fuzz.trimf(error_rate, [-10, -5, 0]),
                  'NS': fuzz.trimf(error_rate, [-5, 0, 5]),
                  'ZE': fuzz.trimf(error_rate, [0, 0, 0]),
                  'PS': fuzz.trimf(error_rate, [0, 5, 10]),
                  'PM': fuzz.trimf(error_rate, [5, 10, 10])}

Kp_sets = {'NB': fuzz.trimf(Kp, [0, 0, 2]),
           'NM': fuzz.trimf(Kp, [0, 2, 4]),
           'NS': fuzz.trimf(Kp, [2, 4, 6]),
           'ZE': fuzz.trimf(Kp, [4, 6, 8]),
           'PS': fuzz.trimf(Kp, [6, 8, 10]),
           'PM': fuzz.trimf(Kp, [8, 10, 10])}

Ki_sets = {'NB': fuzz.trimf(Ki, [0, 0, 0.2]),
           'NM': fuzz.trimf(Ki, [0, 0.2, 0.4]),
           'NS': fuzz.trimf(Ki, [0.2, 0.4, 0.6]),
           'ZE': fuzz.trimf(Ki, [0.4, 0.6, 0.8]),
           'PS': fuzz.trimf(Ki, [0.6, 0.8, 1]),
           'PM': fuzz.trimf(Ki, [0.8, 1, 1])}

Kd_sets = {'NB': fuzz.trimf(Kd, [0, 0, 0.1]),
           'NM': fuzz.trimf(Kd, [0, 0.1, 0.2]),
           'NS': fuzz.trimf(Kd, [0.1, 0.2, 0.3]),
           'ZE': fuzz.trimf(Kd, [0.2, 0.3, 0.4]),
           'PS': fuzz.trimf(Kd, [0.3, 0.4, 0.5]),
           'PM': fuzz.trimf(Kd, [0.4, 0.5, 0.5])}

# 定义模糊规则
rules = [
    fuzz.Rule(error['NB'] & error_rate['NB'], Kp['PM'] & Ki['PM'] & Kd['PM']),
    fuzz.Rule(error['NB'] & error_rate['NM'], Kp['PM'] & Ki['PM'] & Kd['PM']),
    fuzz.Rule(error['NB'] & error_rate['NS'], Kp['PM'] & Ki['PM'] & Kd['PM']),
    fuzz.Rule(error['NB'] & error_rate['ZE'], Kp['PM'] & Ki['PM'] & Kd['PM']),
    fuzz.Rule(error['NB'] & error_rate['PS'], Kp['PM'] & Ki['PM'] & Kd['PM']),
    fuzz.Rule(error['NB'] & error_rate['PM'], Kp['PM'] & Ki['PM'] & Kd['PM']),
    # ...
]

# 输入模糊变量
error_input = -5
error_rate_input = 0

# 模糊化输入
error_fuzzy = fuzz.interp_membership(error.universe, error_input, error_sets)
error_rate_fuzzy = fuzz.interp_membership(error_rate.universe, error_rate_input, error_rate_sets)

# 应用模糊规则
Kp_output, Ki_output, Kd_output = fuzz.defuzz(Kp.universe, fuzz.interp_membership(Kp.universe, error_fuzzy & error_rate_fuzzy, rules), 'centroid'), \
                                  fuzz.defuzz(Ki.universe, fuzz.interp_membership(Ki.universe, error_fuzzy & error_rate_fuzzy, rules), 'centroid'), \
                                  fuzz.defuzz(Kd.universe, fuzz.interp_membership(Kd.universe, error_fuzzy & error_rate_fuzzy, rules), 'centroid')

# 反模糊化输出
Kp_value = Kp_output
Ki_value = Ki_output
Kd_value = Kd_output

# 打印输出
print(f'Kp: {Kp_value}')
print(f'Ki: {Ki_value}')
print(f'Kd: {Kd_value}')

# 5. PID算法的仿真与测试

### 5.1 PID算法仿真平台搭建

PID算法的仿真平台搭建主要涉及以下步骤：

- 选择仿真工具：常用的仿真工具包括MATLAB/Simulink、Python、C++等。
- 建立系统模型：根据被控对象的特性建立数学模型，描述系统输入和输出之间的关系。
- 设计PID控制器：根据系统模型设计PID控制器的参数，包括比例系数、积分系数和微分系数。
- 编写仿真代码：将系统模型、PID控制器和仿真参数编写成仿真代码。
- 运行仿真：运行仿真代码，观察系统输出响应，并分析PID控制器的性能。

### 5.2 PID算法性能评估

PID算法的性能评估主要通过以下指标进行：

- **上升时间（Tr）：**系统从初始状态达到稳态所需的时间。
- **超调量（Ov）：**系统输出在达到稳态之前超过期望值的幅度。
- **调整时间（Ts）：**系统输出在误差范围内保持稳定的时间。
- **稳态误差（Ess）：**系统输出在稳态时与期望值的偏差。

此外，还可以通过以下方法评估PID算法的性能：

- **阶跃响应：**给系统一个阶跃输入，观察系统输出的响应。
- **频率响应：**给系统一个正弦输入，观察系统输出的频率响应。
- **鲁棒性测试：**改变系统参数或输入条件，观察PID控制器的性能是否稳定。

# 6. PID算法在单片机中的应用

### 6.1 单片机PID算法实现方案

单片机实现PID算法主要有两种方式：

- **中断方式：**每隔一定时间（中断周期）对PID算法进行一次计算，然后根据计算结果输出控制信号。这种方式简单易行，但中断周期过长会导致控制精度下降。
- **轮询方式：**在主程序循环中对PID算法进行计算，无需中断。这种方式控制精度较高，但会占用更多的CPU资源。

### 6.2 PID算法在单片机温度控制中的应用实例

以下是一个使用单片机实现PID算法进行温度控制的示例代码：

#include <stdio.h>
#include <stdlib.h>

// PID参数
float Kp = 1.0;
float Ki = 0.1;
float Kd = 0.01;

// 采样时间
float Ts = 0.1;

// 温度传感器输入
float temperature_input;

// PID输出
float pid_output;

// 误差
float error;

// 积分误差
float integral_error = 0.0;

// 微分误差
float derivative_error = 0.0;

// 主函数
int main() {
    // 初始化温度传感器
    temperature_input = 25.0; // 假设初始温度为25摄氏度

    // 循环执行PID算法
    while (1) {
        // 读取温度传感器输入
        temperature_input = read_temperature_sensor();

        // 计算误差
        error = setpoint - temperature_input;

        // 计算积分误差
        integral_error += error * Ts;

        // 计算微分误差
        derivative_error = (error - previous_error) / Ts;

        // 计算PID输出
        pid_output = Kp * error + Ki * integral_error + Kd * derivative_error;

        // 输出控制信号
        output_control_signal(pid_output);

        // 更新上一次误差
        previous_error = error;
    }

    return 0;
}

在这个示例中：

- `Kp`、`Ki`、`Kd`是PID参数。
- `Ts`是采样时间。
- `temperature_input`是温度传感器输入。
- `pid_output`是PID输出。
- `error`是误差。
- `integral_error`是积分误差。
- `derivative_error`是微分误差。
- `setpoint`是设定值。
- `read_temperature_sensor()`是读取温度传感器输入的函数。
- `output_control_signal()`是输出控制信号的函数。