【CSP-S提高组数学模型构建术】：竞赛中建立正确数学模型的独家秘诀


# 摘要
本文旨在全面阐述数学模型构建的系统方法，涵盖从问题的理解与抽象、模型的构建、求解与验证，到模型的优化与评估，以及模型在具体应用中的实践技巧。首先，探讨了数学问题理解的艺术和抽象问题的策略，强调了问题分解的技巧和实际案例的应用。随后，介绍了数学模型构建过程中的假设建立、数学表述及求解验证方法，为模型的构建提供了科学依据。文章接着讨论了数学模型的优化与评估方法，包括灵敏度分析、健壮性检验和评估标准的选择。最后，将数学模型构建理论应用于CSP-S提高组中，分析了竞赛中的实战技巧、高级模型构建策略以及创新思维的培养。通过本文的系统梳理，读者能够掌握构建高效数学模型的理论和实践技能，以适应不同领域的复杂问题解决。

# 关键字
数学模型；问题理解；问题抽象；模型构建；模型求解；模型优化；模型评估；竞赛应用；创新思维

参考资源链接：[近五年CSP-S提高组真题及解析全集下载](https://wenku.csdn.net/doc/agfj268156?spm=1055.2635.3001.10343)
# 1. 数学模型构建术概览

数学模型构建术是将现实世界问题抽象成数学语言的过程，它是一种科学的思考方法和解决问题的技术。在信息技术和工程领域，数学模型的应用贯穿于数据分析、预测、优化等多个方面，是实现复杂系统设计与决策的关键。

## 数学模型的目的和作用

数学模型可以帮助我们理解复杂现象，并预测可能的发展趋势。在实际应用中，通过建立模型，工程师和科学家们可以模拟系统的行为，进行风险评估，或是优化资源分配。数学模型在IT行业的应用广泛，无论是算法开发、网络优化还是数据挖掘，都需要借助数学模型的构建与分析。

## 数学模型的构建框架

模型构建通常遵循以下步骤：定义问题、建立模型、求解模型、验证模型。整个过程是一个迭代的过程，需要在实际应用中不断调整和完善。而数学模型构建术的目标，就是为了指导我们更高效、更准确地完成这个过程。

在后续章节中，我们将深入探讨如何理解和抽象数学问题，构建和求解模型，以及如何优化和评估模型的有效性。通过具体案例，我们将探索数学模型在解决实际问题中的应用。

# 2. 数学问题的理解与抽象

在这一章节中，我们将深入探讨如何理解和抽象数学问题。这包括掌握快速读懂题目的艺术、提取题目中的关键信息、将实际问题转化为数学问题，以及如何通过问题分解的技巧来简化复杂的挑战。

### 2.1 理解问题的艺术

理解问题是一切数学模型构建过程的起点。这个部分将展示如何快速而准确地理解数学题目，并从中提取关键信息。

#### 2.1.1 如何快速读懂题目

在面对一个数学问题时，迅速准确地理解题目的要求至关重要。要做到这一点，需要注意以下几个步骤：

- **通读题目**：首先快速阅读一遍题目，了解问题的背景和大致内容。
- **圈出关键词**：在第二遍阅读时，圈出题目的关键词汇，如给定条件、要求解决的问题等。
- **识别已知与未知**：明确题目中已知信息和需要求解的未知量。
- **理解问题结构**：将问题分解为更小的部分，理解每个部分的作用和相互关系。

例如，考虑一个典型的优化问题：一家公司需要在不同城市之间运输货物，要求找到最短的运输路线。这里的关键信息包括“最短的运输路线”（目标函数）、“不同城市之间”（约束条件）、“运输”（行为动作）。

graph TD
    A[题目背景] -->|阅读| B[圈出关键词]
    B --> C[识别已知与未知]
    C --> D[理解问题结构]
    D --> E[构建模型]

#### 2.1.2 题目中的关键信息提取

成功提取关键信息是解题的第一步。这需要对数学概念有深入的了解，并能够识别数学结构和模式。

- **概念识别**：识别出题目涉及的主要数学概念，如代数、几何、概率等。
- **结构分析**：分析这些概念如何相互作用，以及它们在整个问题中的作用。
- **模式匹配**：寻找题目中熟悉的模式或已知问题的变体，这有助于快速理解问题本质。

举例来说，如果一个题目涉及到等差数列，识别出这一点后可以应用等差数列的公式来简化问题。

### 2.2 抽象问题的策略

将实际问题转化为数学问题是一项关键技能，它涉及到从现实世界的问题中提炼出数学模型。本节将讨论如何实现这一转化，并通过案例来说明实际问题与数学模型之间的连接。

#### 2.2.1 将实际问题转化为数学问题

在实际问题到数学问题的转化中，涉及以下步骤：

- **识别实际问题的关键要素**：分析问题的实际背景，提取出可以量化的关键因素。
- **建立数学关系**：将关键要素之间的关系用数学语言表达出来，如用函数、方程或不等式。
- **简化假设**：在不影响问题本质的前提下进行简化，以降低问题的复杂度。

例如，在一个经济学问题中，将公司成本和收益的关系抽象为函数模型。

flowchart LR
    A[识别关键要素] --> B[建立数学关系]
    B --> C[简化假设]
    C --> D[构建数学模型]

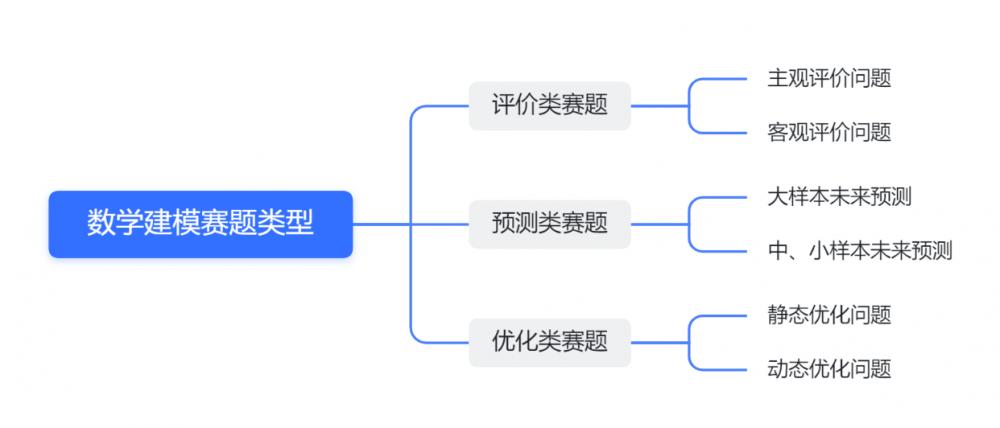
#### 2.2.2 常见问题类型的抽象方法

不同的问题类型需要采取不同的抽象方法。以下是一些常见的问题类型及其对应的抽象方法：

- **优化问题**：确定目标函数和约束条件，使用拉格朗日乘数法、线性规划等方法。
- **统计问题**：定义样本空间、概率分布和统计量，应用期望、方差等概念。
- **动态问题**：构建状态转移方程，使用马尔可夫链、动态规划等技术。

#### 2.2.3 案例分析：实际问题与数学模型的连接

通过具体案例，我们可以看到如何将现实生活中的问题抽象成数学模型。以下是一个案例：

**案例分析：城市交通流量问题**

假设要分析一个城市中主要十字路口的交通流量模式，目的是优化交通信号灯的配置，以减少拥堵。首先，需要收集数据，包括各时段车辆通过路口的数量和方向。然后，将交通流量表示为时间序列数据，并应用概率分布模型来描述不同时间段的交通流量变化。最终，使用优化算法（如遗传算法）对信号灯进行配置，以实现流量最大化。

### 2.3 问题分解的技巧

在处理复杂问题时，将问题分解为更小的模块是一种常用且有效的策略。本节将介绍如何将复杂问题拆分成简单模块、分析模块间关系，并通过案例实操来展示分解和解决问题的过程。

#### 2.3.1 如何将复杂问题拆分成简单模块

分解问题的步骤包括：

- **问题的层次化**：根据问题的结构和要素进行分层，每一层关注不同的细节级别。
- **模块化处理**：将问题的不同部分分隔开来，每个部分作为一个独立模块处理。
- **模块间的接口定义**：确定模块间如何相互作用，包括数据输入输出和依赖关系。

举个例子，将一个复杂的运输问题分解为“货物装载”、“路线规划”和“时间管理”三个模块。

gr