拥塞控制中的梯度下降算法研究

# 1. 网络拥塞控制基础

网络中的拥塞是指网络中的数据流量过大，导致网络设备无法及时处理所有数据包的现象。拥塞控制在网络通信中至关重要，它可以避免网络过载、保障数据传输的稳定性和可靠性。常见的拥塞控制算法包括队列管理算法和TCP拥塞控制算法。队列管理算法通过管理路由器的缓冲区来控制数据包的传输速率，而TCP拥塞控制算法则通过调整拥塞窗口大小来控制数据流量。这些算法在网络中起着至关重要的作用，有效地解决了网络拥塞问题，提高了网络的整体性能和稳定性。在后续章节中，我们将深入探讨梯度下降算法与拥塞控制的结合，以及其在实际应用中的表现。

# 2. 梯度下降算法原理

梯度下降算法是一种常用的优化算法，用于求解函数的最优解。在机器学习和神经网络中，梯度下降算法被广泛应用于参数优化过程。本章将介绍梯度下降算法的基本概念以及批量梯度下降算法的原理。

### 梯度下降概述
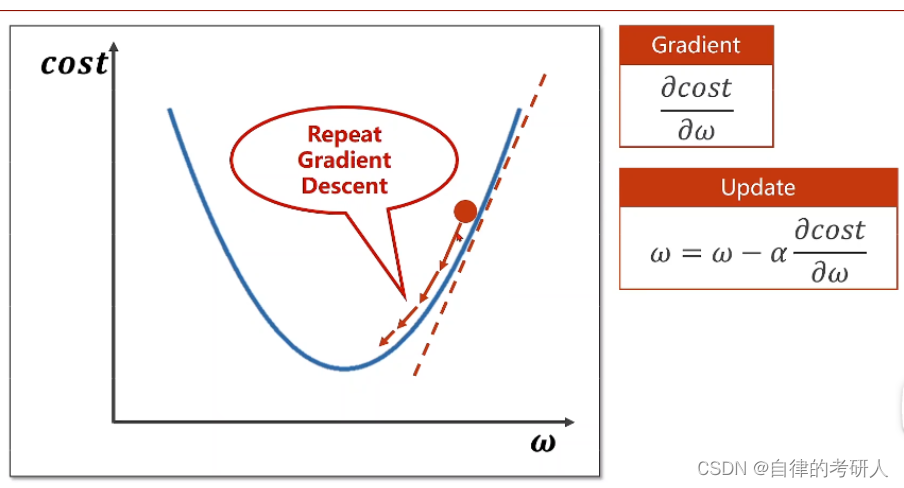
梯度下降是一种基于搜索的优化算法，用于寻找函数的局部最小值。在优化问题中，我们希望通过调整自变量来最小化或最大化目标函数。梯度下降算法通过计算目标函数的梯度方向，并沿着梯度的负方向迭代调整自变量，从而逐步接近最优解。

#### 优化问题背景
优化问题是在给定约束条件下寻找目标函数的最优解。例如，在机器学习中，我们需要最小化损失函数来提高模型的预测性能。

#### 基本思想
梯度下降的基本思想是不断沿着目标函数的梯度方向更新参数，以使函数值逐渐减小。通过迭代优化，最终收敛到局部最优解或全局最优解。

#### 梯度下降示例
假设我们要优化一个简单的二次函数 $f(x) = x^2$，梯度下降会沿着梯度的负方向更新参数。例如，初始值 $x=4$，学习率为 $0.1$，则更新过程为：$x_{new} = x_{old} - \alpha \cdot \nabla f(x) = 4 - 0.1 \cdot 2 \cdot 4 = 3.2$。通过多次迭代，我们可以逐步接近最优解 $x=0$。

### 批量梯度下降算法
批量梯度下降是梯度下降算法的一种形式，它在每一次迭代中都使用全部样本来更新参数。虽然计算开销较大，但通常能获得较稳定的收敛效果。

#### 算法步骤
1. 初始化参数 $\theta$。
2. 计算梯度 $\nabla J(\theta)$。
3. 更新参数：$\theta = \theta - \alpha \cdot \na