【运算放大器稳定性：全面掌握补偿技术】：确保电路稳定运行的黄金法则


参考资源链接：[三级运放架构解析：SMC、SMCNR与NMC的极零点补偿策略](https://wenku.csdn.net/doc/1c6bnjtops?spm=1055.2635.3001.10343)
# 1. 运算放大器稳定性基础

在本章中，我们将揭开运算放大器稳定性的神秘面纱，从基础理论开始，一步步深入探讨运算放大器稳定性的核心要素。首先，我们会了解什么是运算放大器稳定性，以及为什么它对电路性能至关重要。随后，我们将会通过分析开环增益、相位和频率响应等关键因素，来建立稳定性的初步概念。此外，我们会详细探讨在设计过程中，如何通过选择合适的运算放大器和配置外围电路来避免潜在的不稳定问题。通过本章的学习，读者将能够对运算放大器的稳定性有一个清晰和全面的理解，并在实际应用中做出更明智的设计决策。

# 2. 运算放大器的频率响应与补偿

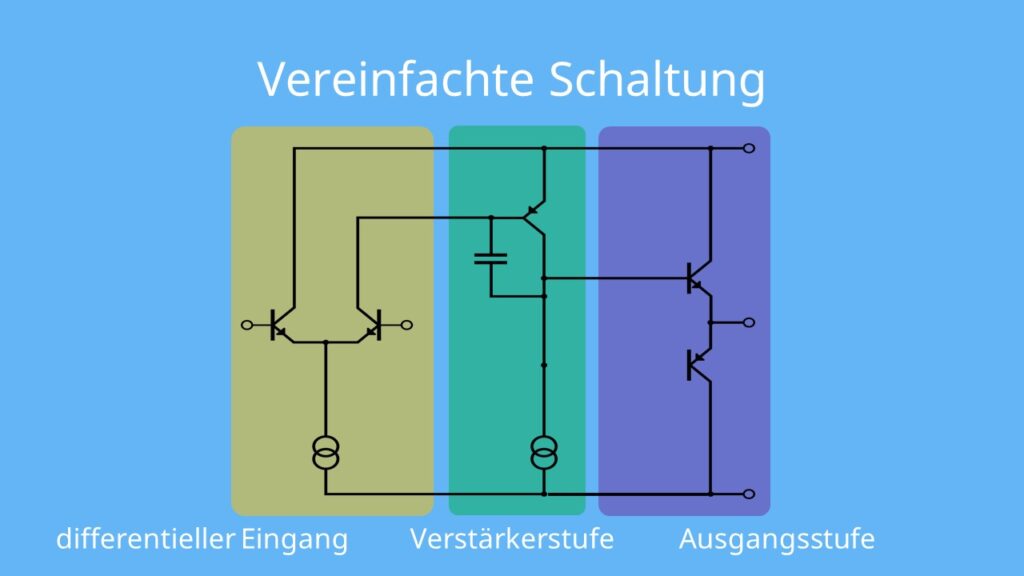
## 2.1 运算放大器的频率响应理论

### 2.1.1 带宽与增益的关系

在分析运算放大器的频率响应时，带宽是一个核心概念。带宽指的是运算放大器能够在不失真情况下放大信号的频率范围，而增益则是放大器放大信号的倍数。在实际应用中，带宽和增益之间存在一种负相关关系，即带宽越大，增益会越小。这种关系是由运算放大器内部电路的设计和制造技术决定的。

具体来说，运算放大器的增益随着频率的增加而下降。在低频区域，增益保持恒定，表现为一个平坦的平台，这一区域称为增益带宽积（GBW）。然而，随着频率继续增加，增益开始下降，运算放大器的放大能力减弱，最终在高频时增益降至1，这一点定义为带宽。

在设计中，当运算放大器用于放大低频信号时，用户可以预设一个较高的增益值而不必担心带宽。但若需要处理的信号频率较高，用户就需要选择一个具有足够带宽的运算放大器，以确保信号在高频下仍能被正确放大。

### 2.1.2 极点和零点对频率响应的影响

为了更好地理解频率响应，需要引入极点和零点的概念。在频域分析中，极点定义为增益降至3dB点的位置，而零点是增益增加的点。运算放大器的频率响应会受到其内部电路极点和零点的影响。

极点对频率响应的影响尤为显著，它决定了运算放大器在特定频率上增益的下降速率。一般来说，运算放大器中第一个极点会确定增益从平坦区域开始下降的转折点。随后的每一个极点都会引起增益曲线在那个频率附近产生一个额外的斜率下降。

零点的作用则相反，它会在其对应的频率点上增加增益，抵消极点的影响。通过合理配置零点，可以改善运算放大器的频率响应特性，例如，通过零点补偿技术来拉平高频增益下降的趋势，增加高频带宽。

## 2.2 补偿技术的基本原理

### 2.2.1 补偿的目的和方法

补偿技术用于稳定运算放大器的频率响应，消除或减少振铃和过冲等不稳定现象。补偿的目的是为了确保运算放大器在整个工作频率范围内提供平稳、无失真的信号放大。

补偿方法通常可以分为外部补偿和内部补偿。外部补偿是指在运算放大器外部通过添加额外的电路元件，如电容和电阻，来改变运算放大器的频率响应。而内部补偿则是将补偿电路集成到运算放大器芯片内部，通常是通过改变内部晶体管的偏置或使用特殊的电路设计来实现。

外部补偿的优点在于灵活性高，可以根据具体的应用需求进行个性化的调整。内部补偿则简化了设计，使用户不需要额外的外部元件就能获得一个比较稳定的工作环境，但是它的调整范围有限，适用于大部分标准应用。

### 2.2.2 典型的补偿电路设计

在讨论典型的补偿电路设计之前，了解基本的电路模型是必要的。一个常见的补偿电路是在运算放大器的反馈路径中插入一个电容，这会引入一个补偿极点，从而改变增益随频率的下降速率。

一个典型的外部补偿电路设计包括一个与运算放大器的输出端串联的电容（Ccomp），和一个与反馈电阻并联的电阻（Rcomp）。通过选择适当的Ccomp和Rcomp的值，可以在特定的频率点产生所需的零点，从而优化频率响应。

举一个简单的例子，如果一个运算放大器需要在更高频率下保持稳定的增益，可以通过减小Ccomp的值来提高第一个极点的位置。而Rcomp则用来调整零点的位置，确保零点在极点之前，以实现有效的频率补偿。

此设计允许工程师在不牺牲过多带宽的情况下，获得更宽的稳定增益范围，从而适用于多种频率敏感的应用场合。

## 2.3 稳定性分析工具

### 2.3.1 相位裕度和增益裕度的概念

在评估运算放大器的稳定性时，相位裕度和增益裕度是两个重要的参数。增益裕度（GM）是指在环路增益达到1（0dB）时，系统相位偏移还能够增加多少度而不失稳。通常情况下，GM越大，系统稳定性越高。

相位裕度（PM）则是指在系统增益为1时，系统相位偏移距离-180度（即系统相位裕度）还有多少度。一般来说，PM大于60度被认为是稳定的。

在实际应用中，这两个参数可以帮助我们了解在特定频率下系统放大信号的能力，以及系统在该频率下是否会产生振铃和过冲等不稳定现象。工程师常常利用这两个参数来设计电路，保证系统既不会太慢也不会太不稳。

### 2.3.2 利用波特图分析稳定性