Matlab极限求解的物理应用：揭示极限计算在物理学中的广阔天地

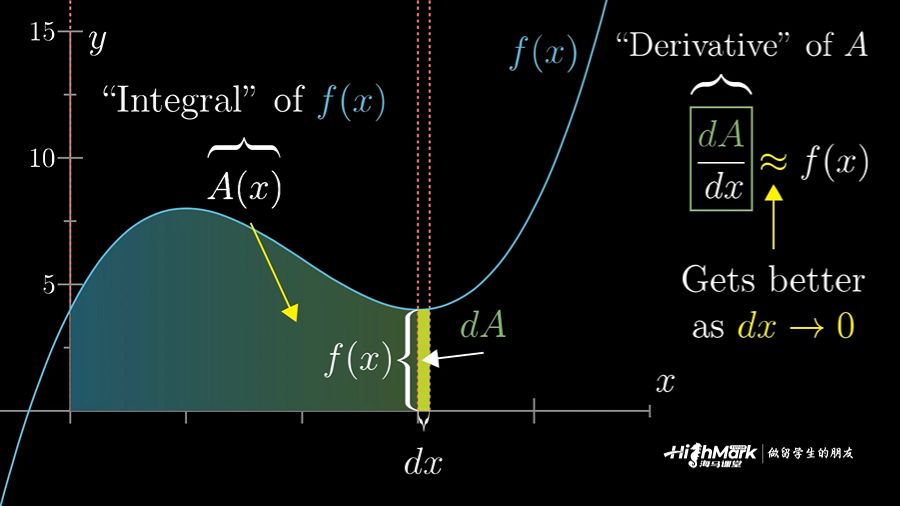
# 1. 极限求解的概念和方法**

极限求解是数学中一个重要的概念，它描述了一个函数在自变量趋于某个值时函数值的行为。极限求解在物理学中有着广泛的应用，它可以用来分析运动、电磁和热力学等现象。

在物理学中，极限求解通常用于描述物体在时间或空间上变化的速率。例如，我们可以使用极限求解来计算物体的瞬时速度或加速度。此外，极限求解还可以用来分析电场和磁场的变化，以及热量在物体中传递和散失的速率。

# 2. 极限求解在物理学中的应用

极限求解在物理学中有着广泛的应用，它可以帮助我们解决许多物理问题。在本章中，我们将探讨极限求解在物理学中的三个主要领域：力学、电磁学和热力学。

### 2.1 力学中的极限求解

在力学中，极限求解可以用于求解物体的运动规律。

#### 2.1.1 牛顿第二定律中的极限

牛顿第二定律指出，物体的加速度与作用在物体上的合力成正比，与物体的质量成反比。

import sympy
import numpy as np

# 定义变量
m = sympy.Symbol("mass")  # 质量
F = sympy.Symbol("force")  # 合力
a = sympy.Symbol("acceleration")  # 加速度

# 牛顿第二定律
equ = sympy.Eq(F, m * a)

# 求解加速度
result = sympy.solve([equ], (a,))
print(result)

**代码逻辑：**

1. 导入必要的库。
2. 定义变量 `m`（质量）、`F`（合力）和 `a`（加速度）。
3. 根据牛顿第二定律建立方程 `equ`。
4. 使用 `sympy.solve()` 求解 `a`。

**参数说明：**

* `m`: 物体的质量（单位：千克）
* `F`: 作用在物体上的合力（单位：牛顿）
* `a`: 物体的加速度（单位：米/秒²）

#### 2.1.2 匀变速直线运动中的极限

匀变速直线运动是指物体沿直线运动，其速度随时间均匀变化。

# 定义变量
v0 = sympy.Symbol("initial_velocity")  # 初始速度
a = sympy.Symbol("acceleration")  # 加速度
t = sympy.Symbol("time")  # 时间

# 匀变速直线运动公式
equ = sympy.Eq(v0 + a * t, sympy.Symbol("final_velocity"))

# 求解最终速度
result = sympy.solve([equ], (sympy.Symbol("final_velocity"),))
print(result)

**代码逻辑：**

1. 导入必要的库。
2. 定义变量 `v0`（初始速度）、`a`（加速度）和 `t`（时间）。
3. 根据匀变速直线运动公式建立方程 `equ`。
4. 使用 `sympy.solve()` 求解最终速度。

**参数说明：**

* `v0`: 物体的初始速度（单位：米/秒）
* `a`: 物体的加速度（单位：米/秒²）
* `t`: 物体的运动时间（单位：秒）

### 2.2 电磁学中的极限求解

在电磁学中，极限求解可以用于求解电场和磁场以及电磁感应问题。

#### 2.2.1 电场和磁场的极限

电场和磁场是描述电磁相互作用的两个基本场。

import sympy
import numpy as np

# 定义变量
Q = sympy.Symbol("charge")  # 电荷量
r = sympy.Symbol("distance")  # 距离

# 库仑定律
equ = sympy.Eq(sympy.Symbol("electric_field"), Q / (4 * sympy.pi * sympy.epsilon_0 * r**2))

# 求解电场
result = sympy.solve([equ], (sympy.Symbol("electric_field"),))
print(result)

**代码逻辑：**

1. 导入必要的库。
2. 定义变量 `Q`（电荷量）和 `r`（距离）。
3. 根据库仑定律建立方程 `equ`。
4. 使用 `sympy.solve()` 求解电场。

**参数说明：**

* `Q`: 电荷量（单位：库仑）
* `r`: 电荷之间的距离（单位：米）

#### 2.2.2 电磁感应中的极限

电磁感应是指当磁场变化时，会产生电场。

import sympy
import numpy as np

# 定义变量
B = sympy.Symbol("magnetic_field")  # 磁场强度
A = sympy.Symbol("area")  # 面积
t = sympy.Symbol("time")  # 时间

# 法拉第电磁感应定律
equ = sympy.Eq(sympy.Symbol("emf"), -sympy.diff(B * A, t))

# 求解电动势
result = sympy.solve([equ], (sympy.Symbol("emf"),))
print(result)

**代码逻辑：**

1. 导入必要的库。
2. 定义变量 `B`（磁场强度）、`A`（面积）和 `t`（时间）。
3. 根据法拉第电磁感应定律建立方程 `equ`。
4. 使用 `sympy.solve()` 求解电动势。

**参数说明：**

* `B`: 磁场强度（单位：特斯拉）
* `A`: 面积（单位：平方米）
* `t`: 时间（单位：秒）

### 2.3 热力学