单片机C语言程序设计数据结构与算法：提升代码效率的秘诀

# 1. 单片机C语言程序设计概述**

单片机C语言程序设计是利用C语言对单片机进行编程，实现特定功能的软件开发过程。它广泛应用于嵌入式系统、工业控制、物联网等领域。

单片机C语言程序设计具有以下特点：

* **资源受限：**单片机通常具有较小的存储空间和处理能力，需要优化代码以提高效率。
* **实时性要求：**单片机系统往往需要对事件做出快速响应，要求程序具有较高的实时性。
* **嵌入式特性：**单片机程序通常嵌入在硬件系统中，需要与硬件设备进行交互。

# 2. 数据结构与算法基础

### 2.1 数据结构的概念和分类

**2.1.1 数组、链表、栈、队列**

数据结构是组织和存储数据的方式，它决定了数据的访问和处理效率。单片机C语言中常用的数据结构包括：

- **数组：**一种线性结构，元素按顺序存储，通过索引访问。
- **链表：**一种非线性结构，元素通过指针连接，支持动态插入和删除。
- **栈：**一种后进先出（LIFO）结构，元素通过栈顶指针访问。
- **队列：**一种先进先出（FIFO）结构，元素通过队头和队尾指针访问。

### 2.2 算法的复杂度分析

**2.2.1 时间复杂度、空间复杂度**

算法的复杂度衡量其执行效率，包括时间复杂度和空间复杂度：

- **时间复杂度：**算法执行所需的时间，通常用大O符号表示，如O(n)、O(n^2)。
- **空间复杂度：**算法执行所需的空间，通常也用大O符号表示，如O(1)、O(n)。

### 2.2.2 算法效率优化

优化算法效率的方法包括：

- **循环展开：**将循环体中的代码复制到循环外，减少循环次数。
- **函数内联：**将函数调用替换为函数体代码，减少函数调用开销。

**代码示例：**

// 循环展开
int sum = 0;
for (int i = 0; i < 10; i++) {
    sum += i;
}

// 展开后的代码
int sum = 0;
sum += 0;
sum += 1;
sum += 2;
sum += 9;

// 函数内联
int square(int x) {
    return x * x;
}

// 内联后的代码
int square(int x) {
    return x * x;
}

**逻辑分析：**

循环展开通过减少循环次数来优化时间复杂度。函数内联通过消除函数调用开销来优化时间复杂度。

# 3. 单片机C语言中数据结构的应用

### 3.1 数组在单片机中的使用

#### 3.1.1 数组的定义、初始化、访问

**定义数组**

在单片机C语言中，数组是一种连续的内存区域，用于存储相同数据类型的多个元素。数组的定义语法如下：

数据类型 数组名[数组大小];

例如，定义一个存储10个整数的数组：

int array[10];

**初始化数组**

数组元素可以在定义时进行初始化，也可以在定义后通过赋值操作进行初始化。

**访问数组元素**

数组元素可以通过下标访问，下标从0开始。数组元素的访问语法如下：

数组名[下标]

例如，访问数组`array`中第5个元素：

array[4];

### 3.2 链表在单片机中的应用

#### 3.2.1 链表的创建、插入、删除

**创建链表**

链表是一种动态数据结构，它由一组节点组成，每个节点包含数据和指向下一个节点的指针。在单片机C语言中，链表的创建需要手动分配内存并管理节点。

**插入节点**

在链表中插入节点需要修改链表结构，将新节点插入到指定位置。

**删除节点**

删除链表中的节点需要修改链表结构，将要删除的节点从链表中移除。

### 3.3 栈和队列在单片机中的应用

#### 3.3.1 栈和队列的实现、操作

**栈**

栈是一种后进先出（LIFO）的数据结构，它通过栈顶指针管理元素的进出。在单片机C语言中，栈可以通过数组或链表实现。

**队列**

队列是一种先进先出（FIFO）的数据结构，它通过队头指针和队尾指针管理元素的进出。在单片机C语言中，队列可以通过数组或链表实现。

# 4. 单片机C语言中算法的应用

在单片机系统中，算法的应用至关重要，它可以帮助优化程序性能，提高程序效率。本章将介绍排序算法、搜索算法和优化算法在单片机C语言中的应用。

### 4.1 排序算法在单片机中的应用

排序算法用于将一组数据按特定顺序排列。在单片机系统中，常用的排序算法包括冒泡排序和快速排序。

#### 4.1.1 冒泡排序

冒泡排序是一种简单的排序算法，它通过比较相邻元素并交换位置来对数据进行排序。其算法流程如下：

graph LR
subgraph 冒泡排序
    A[i] --> A[i+1]
    A[i+1] --> A[i]
    A[i] --> A[i+1]
end

**代码块：**

void bubbleSort(int arr[], int n) {
    int i, j;
    for (i = 0; i < n - 1; i++) {
        for (j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

**逻辑分析：**

* 外层循环 `for (i = 0; i < n - 1; i++)` 遍历数组元素。
* 内层循环 `for (j = 0; j < n - i - 1; j++)` 比较相邻元素。
* 如果 `arr[j]` 大于 `arr[j + 1]`，则交换两个元素。

#### 4.1.2 快速排序

快速排序是一种高效的排序算法，它通过分治法将数组划分为较小的子数组并递归排序。其算法流程如下：

graph LR
subgraph 快速排序
    A[i] --> A[j]
    A[j] --> A[i]
    A[i] --> A[j]
end

**代码块：**

void quickSort(int arr[], int low, int high) {
    if (low < high) {
        int pivot = partition(arr, low, high);
        quickSort(arr, low, pivot - 1);
        quickSort(arr, pivot + 1, high);
    }
}

int partition(int arr[], int low, int high) {
    int pivot = arr[high];
    int i = (low - 1);

    for (int j = low; j <= high - 1; j++) {
        if (arr[j] < pivot) {
            i++;
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }

    int temp = arr[i + 1];
    arr[i + 1] = arr[high];
    arr[high] = temp;

    return (i + 1);
}

**逻辑分析：**

* `partition` 函数将数组划分为两部分，一部分包含小于基准值（`pivot`）的元素，另一部分包含大于基准值的元素。
* `quickSort` 函数递归地对两个子数组进行排序。

### 4.2 搜索算法在单片机中的应用

搜索算法用于在数据集中查找特定元素。在单片机系统中，常用的搜索算法包括顺序搜索和二分搜索。

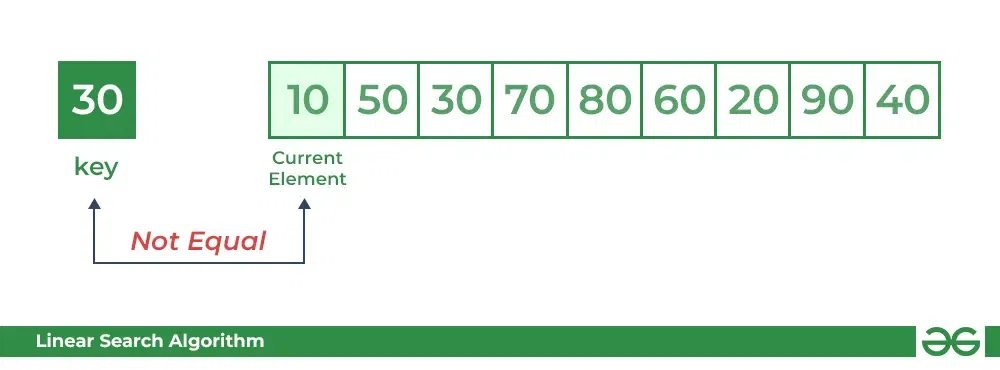
#### 4.2.1 顺序搜索

顺序搜索是一种简单的搜索算法，它通过逐个比较元素来查找特定元素。其算法流程如下：

graph LR
subgraph 顺序搜索
    A[i] --> A[i+1]
    A[i+1] --> A[i]
    A[i] --> A[i+1]
end

**代码块：**

int linearSearch(int arr[], int n, int key) {
    for (int i = 0; i < n; i++) {
        if (arr[i] == key) {
            return i;
        }
    }

    return -1;
}

**逻辑分析：**

* 循环遍历数组元素，比较每个元素是否等于 `key`。
* 如果找到 `key`，则返回其索引。
* 如果没有找到 `key`，则返回 -1。

#### 4.2.2 二分搜索

二分搜索是一种高效的搜索算法，它通过将数据分成两半并递归搜索来查找特定元素。其算法流程如下：

graph LR
subgraph 二分搜索
    A[i] --> A[j]
    A[j] --> A[i]
    A[i] --> A[j]
end

**代码块：**

int binarySearch(int arr[], int n, int key) {
    int low = 0;
    int high = n - 1;

    while (low <= high) {
        int mid = (low + high) / 2;

        if (arr[mid] == key) {
            return mid;
        } else if (arr[mid] < key) {
            low = mid + 1;
        } else {
            high = mid - 1;
        }
    }

    return -1;
}

**逻辑分析：**

* 初始化 `low` 和 `high` 变量，表示数组的范围。
* 在循环中，计算中间索引 `mid`。
* 如果 `arr[mid]` 等于 `key`，则返回 `mid`。
* 如果 `arr[mid]` 小于 `key`，则将 `low` 更新为 `mid + 1`。
* 如果 `arr[mid]` 大于 `key`，则将 `high` 更新为 `mid - 1`。
* 如果循环结束时没有找到 `key`，则返回 -1。

### 4.3 优化算法在单片机中的应用

优化算法用于提高算法的效率和性能。在单片机系统中，常用的优化算法包括循环展开和函数内联。

#### 4.3.1 循环展开

循环展开是一种优化技术，它将循环体中的代码复制到循环之外。这可以减少循环开销，提高性能。

**代码块：**

// 循环展开前
for (int i = 0; i < n; i++) {
    a[i] = b[i] + c[i];
}

// 循环展开后
a[0] = b[0] + c[0];
a[1] = b[1] + c[1];
a[2] = b[2] + c[2];
a[n-1] = b[n-1] + c[n-1];

**逻辑分析：**

* 将循环体中的代码复制到循环之外。
* 减少了循环开销，提高了性能。

#### 4.3.2 函数内联

函数内联是一种优化技术，它将函数调用直接替换为函数体。这可以减少函数调用开销，提高性能。

**代码块：**

// 函数内联前
int sum(int a, int b) {
    return a + b;
}

int main() {
    int x = sum(1, 2);
}

// 函数内联后
int main() {
    int x = 1 + 2;
}

**逻辑分析：**

* 将函数调用替换为函数体。
* 减少了函数调用开销，提高了性能。

# 5. 单片机C语言程序设计实践**

**5.1 基于数据结构和算法的单片机程序设计**

**5.1.1 数据采集与处理**

数据采集是单片机系统中常见的任务，需要使用适当的数据结构和算法来实现。

**数据采集方法：**

- **模拟信号采集：**使用ADC将模拟信号转换为数字信号。
- **数字信号采集：**使用GPIO或中断直接读取数字信号。

**数据结构：**

- **数组：**存储采集到的数据，方便后续处理。
- **链表：**存储不规则数据，如传感器读数。

**算法：**

- **平均值计算：**使用数组存储数据，计算数组元素的平均值。
- **最大值/最小值查找：**使用链表存储数据，遍历链表查找最大值或最小值。
- **数据过滤：**使用移动平均或卡尔曼滤波器等算法过滤噪声。

**5.1.2 控制系统设计**

单片机广泛用于控制系统中，需要使用数据结构和算法来实现控制逻辑。

**控制算法：**

- **PID控制：**使用比例、积分、微分算法调节输出。
- **模糊控制：**使用模糊逻辑规则实现控制。
- **神经网络控制：**使用神经网络模型实现自适应控制。

**数据结构：**

- **状态机：**存储控制系统的状态，根据输入触发状态转换。
- **队列：**存储控制指令，按先进先出原则执行。

**示例代码：**

// 数据采集和处理
uint16_t adc_data[100];
float avg_adc_data;

void adc_init() {
    // ADC初始化代码
}

void adc_data_collect() {
    for (int i = 0; i < 100; i++) {
        adc_data[i] = ADC_Read();
    }
}

void adc_data_process() {
    avg_adc_data = 0;
    for (int i = 0; i < 100; i++) {
        avg_adc_data += adc_data[i];
    }
    avg_adc_data /= 100;
}

// 控制系统设计
enum state {
    STATE_INIT,
    STATE_RUN,
    STATE_STOP
};

struct queue {
    uint8_t data[10];
    uint8_t head;
    uint8_t tail;
};

void queue_init(struct queue *q) {
    q->head = 0;
    q->tail = 0;
}

void queue_push(struct queue *q, uint8_t data) {
    q->data[q->tail] = data;
    q->tail = (q->tail + 1) % 10;
}

uint8_t queue_pop(struct queue *q) {
    uint8_t data = q->data[q->head];
    q->head = (q->head + 1) % 10;
    return data;
}

void control_system() {
    enum state current_state = STATE_INIT;
    struct queue command_queue;

    queue_init(&command_queue);

    while (1) {
        switch (current_state) {
            case STATE_INIT:
                // 初始化代码
                break;
            case STATE_RUN:
                // 执行控制逻辑
                break;
            case STATE_STOP:
                // 停止控制
                break;
        }

        // 处理队列中的命令
        while (!queue_empty(&command_queue)) {
            uint8_t command = queue_pop(&command_queue);
            switch (command) {
                case CMD_START:
                    current_state = STATE_RUN;
                    break;
                case CMD_STOP:
                    current_state = STATE_STOP;
                    break;
            }
        }
    }
}