R语言数据包coxph进阶：掌握图形化生存分析与结果解释

# 1. coxph包基础介绍

在生存分析的庞大领域内，`coxph`包在R语言统计软件中占据了重要的位置。本章节将作为全书的起点，为读者提供对`coxph`包的初步认识。`coxph`包全称是Cox比例风险模型（Cox Proportional Hazards），它是一种用于分析生存时间数据的半参数模型，广泛应用于医学研究、生物统计学和可靠性工程等领域。

我们将从`coxph`包的安装和加载开始，简述如何在R环境中调用这一工具包进行生存数据的初步分析。接着，通过实例演示如何建立一个基础的Cox比例风险模型，并解读模型输出结果的基本组成部分。这一章的目的是为读者搭建一个理解后续章节复杂内容的基础框架。

以下是`coxph`包的一个简单使用示例：

# 安装和加载coxph包
install.packages("survival")
library(survival)

# 假设数据集为lung
data(lung)
# 建立Cox比例风险模型
cox_model <- coxph(Surv(time, status) ~ age + sex + ph.ecog, data = lung)
summary(cox_model)  # 查看模型详细结果

在这个例子中，`Surv(time, status)`定义了生存时间及其状态，`~` 后面的`age + sex + ph.ecog`是模型中的协变量，它们将被用来解释生存时间的变化。本章将以浅入深的方式，让读者理解上述代码背后的逻辑。

# 2. coxph模型的理论基础

### 2.1 生存分析的基本概念
生存分析是一种统计分析方法，主要用于研究生存时间以及与生存时间相关的影响因素。它广泛应用于医学、生物、金融等多个领域。在这一部分，我们将深入理解生存时间与事件发生的含义，以及生存函数与风险函数的构建和应用。

#### 2.1.1 生存时间与事件发生

生存时间是指从某一特定的起始时间点到某一终点事件发生的时间长度。例如，可以是从确诊癌症开始到患者死亡的这段时间，也可以是从手术完成到恢复健康的这段时间。生存时间的关键特性是右删失，意味着在研究结束时，一些个体并未经历感兴趣的事件，因此我们无法观测到他们的完整生存时间。

在定义生存时间时，我们通常会定义感兴趣的事件，比如死亡、疾病复发或机械故障等。这些事件在生存分析中被称为终点事件。

#### 2.1.2 生存函数与风险函数

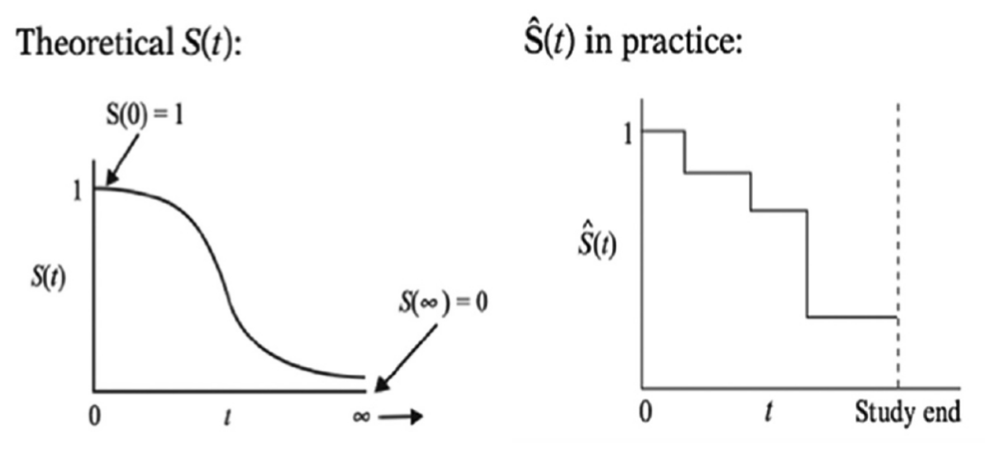
生存函数，通常表示为S(t)，是指在时间t或之前尚未发生感兴趣事件的概率。生存函数是衡量生存时间分布的重要指标。对于一个特定的时间点，生存函数值越低，意味着在该时间点之前发生事件的概率越高。

风险函数（或称为危险函数），通常表示为h(t)，是指在时间t时，在该时刻仍然存活的个体发生感兴趣事件的瞬时发生率。风险函数能够告诉我们，在任意给定的时间点，个体发生事件的可能性有多大。

在生存分析中，我们经常使用Kaplan-Meier法来估计生存函数，使用Nelson-Aalen法来估计风险函数。

### 2.2 cox比例风险模型原理

Cox比例风险模型，简称为Cox模型，是由D.R. Cox于1972年提出的，这是一种半参数模型，它假设风险比（hazard ratio）是时间的函数，并且考虑了协变量的影响，但不假定生存时间的分布形式。

#### 2.2.1 比例风险假设

比例风险假设是Cox模型的基础。它假设不同个体的风险比（即生存风险的比例）在所有时间点都是恒定的。这意味着任何两个个体的风险比随时间的函数图是平行的。这个假设允许模型在不需要具体生存时间分布形式的情况下，就能够估计协变量对生存时间的影响。

比例风险假设的检验通常是使用Schoenfeld残差来进行，如果模型违反了这个假设，就需要考虑使用时间依赖协变量或其它非比例风险模型。

#### 2.2.2 cox模型的数学表达

Cox模型可以表达为：

h(t, X) = h0(t)exp(β1X1 + β2X2 + ... + βpXp)

其中，h(t, X)是风险函数；h0(t)是基线风险函数，即所有协变量值为0时的风险函数；exp(β1X1 + β2X2 + ... + βpXp)是协变量的影响部分，表示协变量对风险的相对影响。

在该模型中，系数β的估计并不依赖于基线风险函数h0(t)的具体形式，这也是Cox模型“半参数”名称的由来。使用最大偏似然估计（partial likelihood estimation）来估计模型参数。

### 2.3 coxph模型的统计推断

统计推断是生存数据分析中的重要步骤，它包括参数估计、标准误差、假设检验和模型诊断等。

#### 2.3.1 参数估计与标准误

参数估计是通过最大似然方法得到模型中未知参数的估计值。标准误（standard error）是对参数估计值的标准偏差的估计，它可以用来进行统计检验和建立置信区间。

#### 2.3.2 假设检验与模型诊断

假设检验主要用来评估模型中协变量是否显著影响生存时间。常用的是Wald检验、似然比检验（likelihood ratio test）和score检验。

模型诊断的目的是检查模型是否适当拟合数据。其中包括比例风险假设检验，如果违反了该假设，则需要考虑模型的进一步改进。还有基于残差的模型拟合优度检验，如Schoenfeld残差检验。

为了具体展示Cox模型的理论基础，下面给出一个Cox模型的R实现示例：

# 安装并加载survival包
install.packages("survival")
library(survival)

# 示例数据：lung数据集
data(lung)

# 建立coxph模型
cox_model <- coxph(Surv(time, status) ~ age + sex + ph.ecog, data = lung)

# 输出模型结果
summary(cox_model)

在上述代码中，我们首先加载了`survival`包，然后使用`coxph()`函数来建立模型。`Surv()`函数创建了一个生存对象，其中`time`和`status`是数据集中的变量，分别代表生存时间与生存状态（通常1代表事件发生，0代表右删失）。模型中的协变量是`age`、`sex`和`ph.ecog`。最后，我们使用`summary()`函数对模型结果进行总结和分析。

在模型的输出结果中，可以查看每个协变量的估计值、标准误、Wald统计量、自由度和p值等信息，以及基线生存函数的估计。

以上章节内容仅作为对Cox模型理论基础的简要介绍，接下来的章节将深入探讨Cox模型在实际应用中的具体操作和分析。

# 3. coxph模型的图形化分析

## 3.1 生存曲线的绘制与解读

### 3.1.1 Kaplan-Meier生存曲线

Kaplan-Meier曲线是生存分析中最常用的非参数估计方法，它是一种估计生存函数的方法，可以在没有分布假设的情况下，估计随时间变化的生存概率。其核心是通过样本数据来估计累积生存概率，从而描绘出生存曲线。在R语言中，可以使用`survival`包中的`survfit()`函数来绘制Kaplan-Meier曲线。

以下是使用`survfit()`函数绘制Kaplan-Meier生存曲线的基本示例代码：

# 加载survival包
library(survival)

# 假设mydata是已经处理好的包含生存时间和事件发生指示的R数据框
# Surv(time, event)用于创建生存对象，time为生存时间，event为指示变量
# status=1表示事件发生，status=0表示右删失数据（censored）
surv_obj <- Surv(time=mydata$time, event=mydata$status)

# 使用survfit()函数计算Kaplan-Meier估计
km_fit <- survfit(surv_obj ~ 1)

# 绘制Kaplan