掌握LabVIEW中DSP的快速傅里叶变换(FFT)：算法原理与实践，优化你的信号处理流程


# 摘要
本文全面探讨了快速傅里叶变换（FFT）的基础知识、在LabVIEW环境中的应用、实践案例分析、性能优化以及高级应用，并针对LabVIEW项目中的FFT实现问题提供了具体解决方案。文章首先介绍了FFT的基本原理和理论背景，接着详述了如何在LabVIEW中利用内置模块进行FFT实现，并通过案例分析展现了FFT在实时数据采集、声音信号处理和无线信号频谱监测等方面的实际应用。文章进一步探讨了提高FFT计算效率的策略、高级FFT分析技术，并讨论了如何实现自定义FFT算法。最后，文章对LabVIEW与数字信号处理（DSP）技术的未来发展进行了展望，强调了在实时系统和新兴领域中LabVIEW的应用前景和创新可能。

# 关键字
快速傅里叶变换；LabVIEW；信号处理；性能优化；实时数据采集；数字信号处理；虚拟仪器

参考资源链接：[LabVIEW DSP Module入门教程：设计与应用指南](https://wenku.csdn.net/doc/3zy5apb9e5?spm=1055.2635.3001.10343)
# 1. 快速傅里叶变换（FFT）基础

快速傅里叶变换（FFT）是现代数字信号处理中的核心技术之一，它能够将时域信号转换为频域信号，从而便于进行频谱分析。FFT的发明大幅降低了傅里叶变换的计算复杂度，使得实时处理大容量数据成为可能。在本章中，我们将概述FFT的历史背景、理论基础，并简要介绍其在不同领域的应用潜力。通过学习本章，读者将对FFT有初步的认识，并为进一步深入研究和应用FFT打下坚实的基础。

## 1.1 历史背景和重要性

傅里叶变换是数学家让-巴蒂斯特·约瑟夫·傅里叶提出的一个概念，它允许我们将复杂的信号分解为一系列简单正弦波的总和。而快速傅里叶变换作为一种高效的算法，使得这一过程在计算机上得以高效实现，大幅缩短了计算时间，极大地推动了信号处理、图像处理、音频分析和无线通信等领域的进步。

## 1.2 FFT的工作原理

FFT的核心在于利用信号的对称性以及周期性，对计算过程进行优化，减少冗余计算。经典的FFT算法有Cooley-Tukey算法等，它们通过将长序列的变换分解为多个较短序列的变换，实现快速计算。这种方法显著降低了传统离散傅里叶变换（DFT）的计算复杂度，从O(N^2)降低到O(NlogN)，其中N是采样点数。

## 1.3 时间复杂度分析

时间复杂度是衡量算法运行时间随输入规模增长变化趋势的指标。FFT的O(NlogN)复杂度意味着其运行时间的增长速度与输入数据量的对数成正比。相较于原始DFT的O(N^2)复杂度，FFT在处理大规模数据时的效率提升是显而易见的。这种性能提升对于需要进行快速数据处理的实时系统和高精度分析应用尤其重要。

# 2. LabVIEW中的信号处理与FFT

## 2.1 LabVIEW环境简介

### 2.1.1 LabVIEW的用户界面和编程概念

LabVIEW（Laboratory Virtual Instrument Engineering Workbench）是一个由美国国家仪器（National Instruments，简称NI）开发的图形化编程环境。它广泛应用于数据采集、仪器控制，以及工业自动化等领域。LabVIEW的用户界面（Front Panel）和编程代码（Block Diagram）是其两大核心元素。

**用户界面（Front Panel）**
用户界面是LabVIEW程序的可视部分，提供了与最终用户交互的前端。用户可以通过控件（如按钮、滑动条、图表等）输入数据，也可以通过指示器（如图表、LED等）查看数据和结果。这是LabVIEW区别于传统文本编程语言的一个显著特点。

**编程代码（Block Diagram）**
代码部分是LabVIEW程序的“幕后”工作区域，由一系列的图形化函数和结构组成，形成了数据流编程模型。在这里，程序员可以使用各种内置的函数节点（Function Nodes）和结构（如While Loop、For Loop、Case Structure等）来设计程序的逻辑和数据流动。

### 2.1.2 基于图形的编程范式

LabVIEW的编程范式基于图形和数据流，而非传统编程语言的顺序执行文本代码。它使工程师能够使用图形化的编程块来快速构建应用程序，尤其是那些涉及到实时数据采集和仪器控制的应用。

图形化编程有几个关键优势：
- **直观性**：图形化编程使得程序逻辑对于新手和非程序员来说更加容易理解。
- **快速开发**：使用预构建的函数库可以快速实现复杂功能，加快开发速度。
- **并行执行**：数据流编程自然支持并行处理，这对于多核心处理器和实时系统至关重要。

## 2.2 FFT算法的理论基础

### 2.2.1 傅里叶分析的历史和重要性

傅里叶分析是数学中一个强大的工具，它能够将复杂的周期函数或信号分解为一系列简单的正弦波。这个过程被称为傅里叶级数。

傅里叶分析的历史可以追溯到19世纪初，由法国数学家让-巴蒂斯特·约瑟夫·傅里叶提出。它的主要贡献在于提供了一种方式，可以将任何周期函数分解为其构成的正弦和余弦函数（基本频率和各阶谐波）的和。

在信号处理领域，傅里叶分析至关重要，因为它允许工程师从频域角度理解信号，这对于滤波、噪声减少、频谱分析等领域是必不可少的。

### 2.2.2 FFT算法的工作原理

快速傅里叶变换（FFT）是傅里叶分析中的一种高效算法。它使得在计算机上计算离散傅里叶变换（DFT）变得非常快速和实用。FFT算法由詹姆斯·W·库利和约翰·W·图基于1965年提出。

DFT是将时域中的信号转换到频域，其公式如下：

\[ X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-j\frac{2\pi}{N}kn} \]

其中，\( x[n] \) 是时域信号的样本，\( X[k] \) 是对应的频域表示，\( N \) 是样本点的总数。

FFT算法通过一种高效的递归分解方式，大幅减少了DFT的计算量。对于一个长度为\( N \)的序列，经典的DFT算法需要进行\( N^2 \)次复数乘法，而FFT算法只需要\( N \log N \)次。

### 2.2.3 时间复杂度分析

傅里叶变换的时间复杂度直接关系到其在实际应用中的可行性。一个\( N^2 \)的时间复杂度对于大规模数据来说是不可接受的，因为它意味着计算量随数据长度的增加呈二次方增长。

FFT算法的时间复杂度为\( N \log N \)，这使得它能够处理比DFT大得多的数据集。在现代计算机中，\( \log N \)的增长几乎可以忽略不计，因此FFT算法可以非常快速地完成计算。

例如，一个长度为1024的序列：
- 使用DFT需要约1百万次复数乘法。
- 使用FFT只需要约1万次复数乘法。

这样的效率提升对于现代通信、图像处理等领域来说至关重要。

## 2.3 实现FFT的LabVIEW模块

### 2.3.1 使用LabVIEW内置FFT函数

在LabVIEW环境中，内置的FFT函数位于函数选板的信号处理子选板中。使用这个函数可以非常方便地对信号进行快速傅里叶变换。其步骤如下：

1. **打开LabVIEW** 并创建一个新的VI（虚拟仪器）。
2. **定位到信号处理函数选板**：通常在编程->函数选板->信号处理路径下。
3. **选择FFT VI**：这个VI将执行FFT转换。
4. **连接输入和输出**：将时域信号数组连接到FFT VI的输入端，FFT VI将输出频域信号数组。

在使用FFT VI之前，需要准备时域信号数组。通常通过数据采集VI获取信号样本或通过模拟函数生成测试信号样本。

### 2.3.2 调整参数和配置FFT分析

FFT VI提供了许多配置选项，以适应不同的分析需求。主要参数包括：

- **长度**：FFT操作的点数。
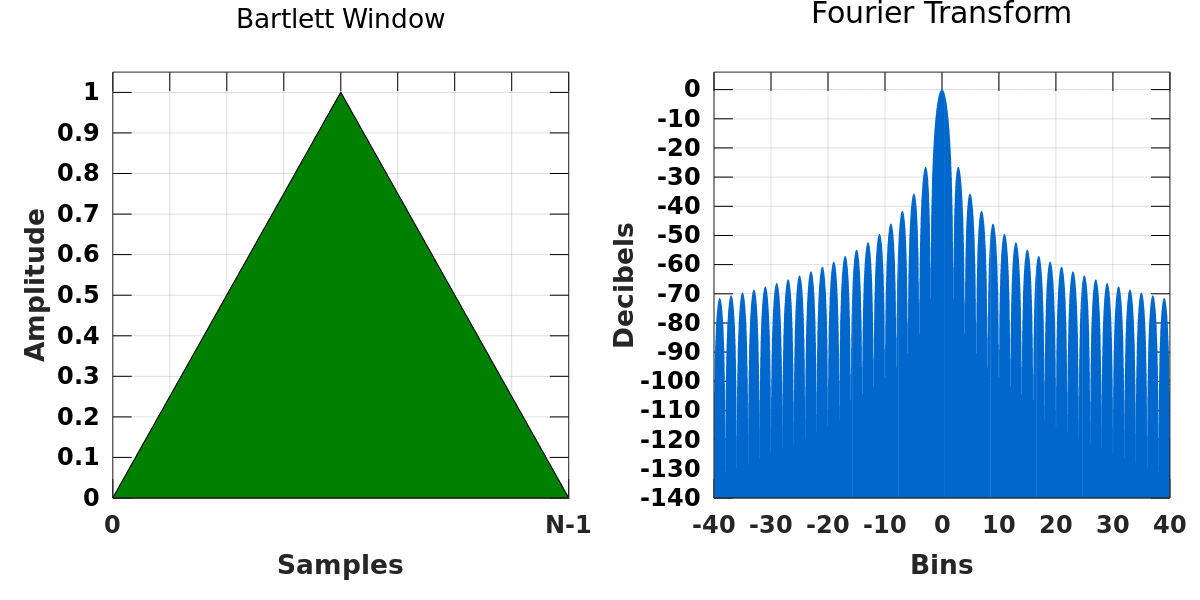
- **窗函数**：用于减少频谱泄露的函数。
- **变换类型**：正向FFT（时域到频域）或逆向FFT（频域到时域）。
- **排列方式**：输入信号样本的排列顺序。

为了得到准确的FFT结果，可能需要根据具体情况调整这些参数。

- **调整FFT长度**：FFT的长度应该与信号的周期特性相匹配。理想情况下，长度应该是信号周期的整数倍。
- **选择窗函数**：不同的窗函数会影响频谱的形状，特别是主瓣和旁瓣宽度。
- **设置变换类型**：根据分析的目的，选择是进行正