OpenCV图像轮廓点坐标提取：从图像中提取轮廓点坐标的扩展应用

# 1. OpenCV图像轮廓概述**

图像轮廓是描述图像中对象形状和边界的重要特征。在计算机视觉中，轮廓提取是指从图像中提取这些轮廓的过程。OpenCV（Open Source Computer Vision Library）是一个流行的计算机视觉库，它提供了丰富的轮廓提取功能。

OpenCV中的轮廓表示为一组连续的点，这些点连接起来形成对象的外边界。轮廓可以用来描述对象的形状、大小、位置和方向等信息。轮廓提取在许多计算机视觉应用中至关重要，例如对象检测、跟踪、分割和分析。

# 2. 图像轮廓点坐标提取理论

### 2.1 轮廓的概念和特征

**概念：**

轮廓是指图像中物体边界或区域的形状轮廓。它是一条连接图像中所有边界像素的闭合曲线。

**特征：**

* **闭合性：**轮廓是一条闭合曲线，始于并终于同一像素。
* **连通性：**轮廓上的所有像素都彼此相邻，没有断点。
* **方向性：**轮廓具有方向性，沿着边界像素的顺序排列。
* **形状：**轮廓的形状可以是规则的（如圆形、矩形）或不规则的。

### 2.2 轮廓提取算法

#### 2.2.1 边缘检测

边缘检测是轮廓提取的第一步。它通过识别图像中像素灰度值的突然变化来检测图像中的边缘。常用的边缘检测算法包括：

* **Sobel算子：**使用一阶导数近似来检测边缘。
* **Canny算子：**一种多步算法，包括降噪、梯度计算、非极大值抑制和滞后阈值化。
* **Laplacian算子：**使用二阶导数近似来检测边缘。

#### 2.2.2 轮廓跟踪

边缘检测后，需要跟踪边缘像素以形成轮廓。常用的轮廓跟踪算法包括：

* **链式编码：**将轮廓像素编码为一系列方向代码，描述轮廓的形状。
* **Douglas-Peucker算法：**一种递归算法，通过迭代去除不必要的轮廓点来简化轮廓。
* **Ramer-Douglas-Peucker算法：**Douglas-Peucker算法的一种变体，使用最大允许误差来简化轮廓。

**代码块：**

import cv2

# 使用Canny算子进行边缘检测
edges = cv2.Canny(image, 100, 200)

# 使用轮廓跟踪算法查找轮廓
contours, hierarchy = cv2.findContours(edges, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)

# 遍历轮廓并绘制
for contour in contours:
    cv2.drawContours(image, [contour], -1, (0, 255, 0), 2)

**逻辑分析：**

* `cv2.Canny()`函数使用Canny算子进行边缘检测，并返回一个二值图像，其中边缘像素为白色，其他像素为黑色。
* `cv2.findContours()`函数使用链式编码算法查找轮廓，并返回一个轮廓列表和一个层次结构。
* `cv2.drawContours()`函数绘制轮廓到图像上。

**参数说明：**

* `image`：输入图像。
* `edges`：边缘检测后的图像。
* `contours`：轮廓列表。
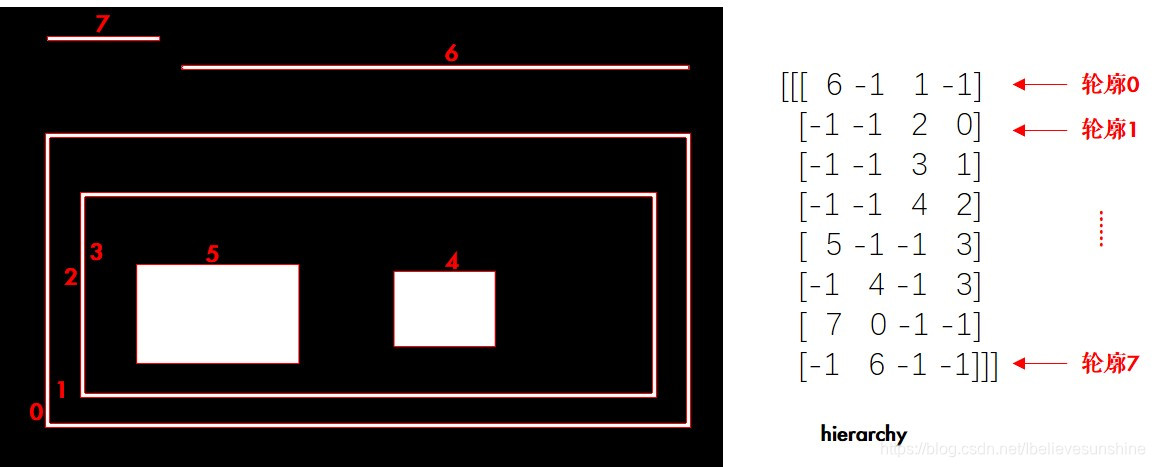
* `hierarchy`：轮廓层次结构。

# 3.1 OpenCV中的轮廓提取函数

OpenCV提供了丰富的轮廓提取函数，其中最常用的有以下几个：

- **cv2.findContours()**：用于查找图像中的轮廓。它返回一个轮廓列表，每个轮廓都是一个由点组成的数组。
- **cv2.drawContours()**：用于在图像上绘制轮廓。它可以根据指定的颜色和厚度绘制轮廓。
- **cv2.approxPolyDP()**：用于对轮廓进行多边形逼近。它可以将轮廓近似为多边形，减少轮廓点的数量。
- **cv2.arcLength()**：用于计算轮廓的长度。它返回轮廓的周长。
- **cv2.contourArea()**：用于计算轮廓的面积。它返回轮廓所包围的区域。

### 3.2 轮廓点坐标的获取

获取轮廓点坐标的方法有两种：

1. **直接访问轮廓数组**：轮廓是一个由点组成的数组，可以通过索引直接访问每个点的坐标。例如：

import cv2

# 加载图像
image = cv2.imread('image.jpg')

# 查找轮廓
contours, hierarchy = cv2.findContours(image, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)

# 获取第一个轮廓的点坐标
points = contours[0]

# 遍历点坐标
for point in points:
    x, y = point[0]
    print(f'点坐标：({x}, {y})')

2. **使用轮廓迭代器**：OpenCV提供了轮廓迭代器，可以遍历轮廓中的所有点。例如：

import cv2

# 加载图像
image = cv2.imread('image.jpg')

# 查找轮廓
contours, hierarchy = cv2.findContours(image, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)

# 获取第一个轮廓的点坐标
contour = contours[0]

# 使用轮廓迭代器遍历点坐标
for point in contour:
    x, y = point[0]
    pri