【围棋博弈中的启发式搜索】：PlantomGo中启发式算法的应用


# 摘要
本文对围棋博弈中启发式搜索算法进行了全面的介绍和分析。首先概述了启发式搜索的基本理论，包括其定义、发展历程、分类及特点。接着，重点介绍了PlantomGo启发式算法的架构、搜索策略以及性能评估。在实战应用与优化方面，本文探讨了启发式搜索在围棋实战中的应用，并提供了一些算法优化技巧，同时展望了启发式搜索结合深度学习的未来趋势。最后，本文还探索了启发式算法在围棋之外的应用领域，强调了其在AI发展中的重要性。通过对启发式算法的研究，本文旨在提升围棋AI的性能，推动AI领域技术进步，并加深对启发式算法教育意义的理解。

# 关键字
围棋博弈；启发式搜索；算法分类；PlantomGo；性能评估；深度学习；AI应用

参考资源链接：[幻影围棋：计算机博弈大赛亚军代码开源](https://wenku.csdn.net/doc/nywfavewpn?spm=1055.2635.3001.10343)
# 1. 围棋博弈与启发式搜索概述

围棋，这一古老的智力游戏，一直以来都是人类与人工智能领域较量的重要战场。随着计算机技术的飞速发展，如何利用启发式搜索算法提高围棋AI的博弈水平成为了一个重要的研究课题。本章节旨在为读者提供一个基础的概念框架，梳理围棋与启发式搜索的关系，并为后续章节中更深入的探讨铺垫理论基础。

在探讨围棋博弈时，离不开对启发式搜索的理解。启发式搜索是人工智能中一种利用经验法则来指导搜索过程的策略，它能够在搜索空间巨大且搜索时间受限的情况下，帮助我们快速找到可接受的解。在围棋这种动态策略游戏中，启发式搜索算法为AI提供了一种分析棋局并制定策略的方法。

启发式算法虽然不能保证找到最优解，但其高效性在围棋AI中的应用已经取得了显著的成就。在本章中，我们将先简要介绍启发式搜索的基本概念，然后重点分析启发式算法在围棋博弈中的应用，以及当前面临的挑战，为读者呈现启发式搜索在围棋领域的全貌。在下一章节中，我们将深入探讨启发式算法的理论基础，为理解其在围棋AI中的应用打下坚实的基础。

# 2. 启发式算法基础理论

在这一章节中，我们将深入探讨启发式算法的基础理论，包括其定义、发展历程、分类以及在围棋领域的应用挑战。这一章节旨在为读者提供对启发式算法的全面理解，不仅是作为一个技术工具，而且作为一个对问题求解和决策过程具有指导意义的理论体系。

## 2.1 启发式搜索的定义与发展

### 2.1.1 启发式搜索的定义

启发式搜索是一种用于解决搜索问题的算法方法，它通过使用启发式信息（heuristic information），即关于问题的“经验法则”，来指导搜索过程，以期在复杂的搜索空间中高效地找到解决方案。这种信息通常是基于问题的特定知识，而不是通过穷举搜索来获得。启发式算法不同于确切算法（如广度优先搜索和深度优先搜索），因为它们不能保证找到最优解，但它们在求解大规模问题时，往往可以更快地找到一个可接受的解。

### 2.1.2 算法的发展历程

启发式搜索算法的发展史与计算机科学和人工智能的发展紧密相连。早期的算法如贪心搜索和最佳优先搜索，都是基于简单的启发式信息进行指导。随着计算能力的提升和问题复杂度的增加，算法的发展逐渐聚焦于提高搜索效率和解的质量。20世纪60年代到80年代，A*搜索算法的提出标志着启发式搜索的成熟，而21世纪初蒙特卡洛树搜索（MCTS）在围棋等游戏中的成功应用，则显示了启发式搜索算法在不确定环境下的巨大潜力。

## 2.2 启发式算法的分类与特点

### 2.2.1 贪心算法

贪心算法是最简单的启发式算法之一。它在每一步选择中都采取当前状态下最好或最优（即最有利）的选择，从而希望导致结果是全局最好或最优的算法。贪心算法并不保证会得到最优解，其效率依赖于问题的具体情况。在某些问题上，贪心算法能够获得最优解，但对于其他问题来说，贪心算法可能只能得到次优解。

### 2.2.2 A*搜索算法

A*搜索算法是一种利用启发式函数来评估节点在图形中到达目标的成本的算法。它被广泛用于路径搜索和图遍历。A*算法的效率来自于其启发式函数的设计，该函数需要满足“可采纳性”（admissibility）条件，即实际成本从当前节点到达目标节点的下限。A*算法是完备的，当存在解时，它总会找到解，并且是最优的。这一点，结合其较优的性能，使得A*算法成为解决许多优化问题的首选方法。

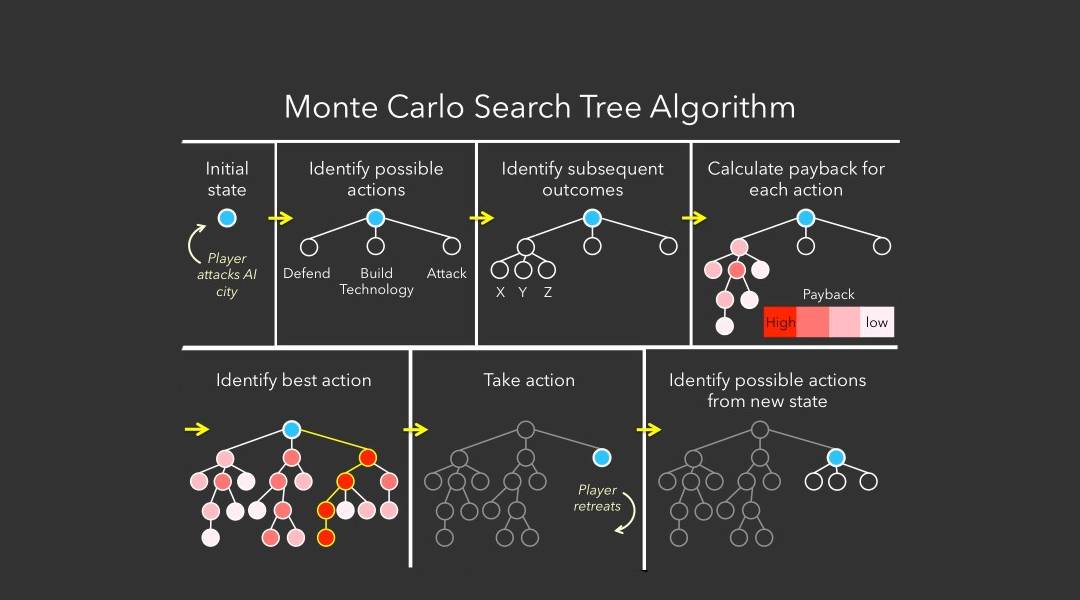
### 2.2.3 蒙特卡洛树搜索（MCTS）

蒙特卡洛树搜索（MCTS）是一种比较现代的启发式搜索算法，它利用随机模拟来探索可能的路径，并通过树状结构来优化搜索方向。MCTS不需要传统的启发式评估函数，而是依靠统计和随机模拟来评估节点的好坏。MCTS因其在围棋和其他复杂游戏中的成功应用而受到广泛关注，特别是在AlphaGo击败李世石后，MCTS引起了全球对人工智能的极大兴趣。

## 2.3 启发式算法在围棋中的挑战

### 2.3.1 围棋的复杂性分析

围棋的复杂性源于其庞大的搜索空间和难以预测的游戏局势。围棋棋盘的大小为19x19，这意味着可能的落子组合数量是天文数字级别的。此外，围棋游戏的策略和战术丰富多变，不仅仅依赖于局部的棋型，还需要对全局棋局的把控。这些特性使得围棋成为测试启发式算法性能的理想平台。

### 2.3.2 启发式算法的局限性

尽管启发式算法在许多领域取得了成功，但其在围棋等复杂游戏中仍面临许多挑战。主要挑战包括如何设计一个有效的启发式函数，以及如何处理局部搜索与全局策略之间的平衡。另外，围棋游戏中存在大量不确定性和模糊性，这使得传统的基于确切计算的算法难以应对。因此，启发式算法需要不断地适应和改进，以应对这些挑战。

在本章节中，我们简要介绍了启发式搜索算法的定义、发展历程、分类及其特点，并针对围棋这种复杂游戏的特定挑战进行了探讨。接下来，我们将深入探讨PlantomGo启发式算法的架构和围棋策略，以及该算法的性能评估，进而分析启发式算法在围棋实战中的具体应用与优化策略。

# 3. PlantomGo启发式算法详解

## 3.1 PlantomGo算法架构
### 3.1.1 算法原理
PlantomGo是一种在围棋游戏领域应用的启发式搜索算法，其核心在于模仿人类棋手的直觉和经验，通过评估棋局的潜在价值来进行决策。算法的目标是找到最优的落子位置，以最大化己方的胜率或优势。

算法利用棋局状态树对所有可能的走法进行评估，每个节点代表一种特定的棋局状态，通过评估函数对每个节点进行价值评分，指导搜索向最有希望的方向发展。评估函数考虑了诸如棋型、活棋、死棋、气的数量和棋子的连接等因素。

### 3.1.2 算法核心组成部分
PlantomGo的算法架构主要由以下几个核心部分组成：

1. 搜索引擎：负责遍历状态空间，并使用启发式评估函数来确定搜索方向。
2. 评估函数：用于评估当前棋局状态的价值，并引导搜索过程。
3. 走法生成器：负责生成给定棋局状态下所有合法的走法。
4. 剪枝策略：以减少搜索树的大小，提高搜索效率。

## 3.2 启发式搜索与围棋策略
### 3.2.1 搜索策略优化
在围棋游戏中，搜索策略至关重要。为了在有限的时间内找到最佳落子点，搜索策略需要优化以考虑以下因素：

- **深度优先与广度优先的平衡**：在搜索初期进行广度优先搜索以探索