XPS峰拟合的统计学原理：误差分析与模型选择的智慧


# 摘要
X射线光电子能谱（XPS）峰拟合是一种分析材料表面化学状态的技术，对理解和优化材料特性具有重要意义。本文首先介绍了XPS峰拟合理论的基础，并探讨了统计学方法在XPS峰拟合中的应用，如误差分析和模型选择。随后，本文详细阐述了XPS峰拟合实践操作，包括软件使用和案例分析。进一步地，文章深入探讨了XPS峰拟合模型的参数估计、稳健性分析以及交叉验证技术。最后，文章展望了人工智能与机器学习在XPS峰拟合中的潜在应用以及未来技术发展趋势，强调了跨学科技术融合对峰拟合技术进步的重要性。

# 关键字
XPS峰拟合；统计学；误差分析；模型选择；稳健性分析；人工智能；机器学习

参考资源链接：[XPSPeak41峰拟合教程：从导入到数据输出的详细步骤](https://wenku.csdn.net/doc/59css4rwfc?spm=1055.2635.3001.10343)
# 1. XPS峰拟合理论基础

XPS（X射线光电子能谱）峰拟合是表面科学分析中的一项关键技术，通过理论模型的构建与优化，能够在原子层面上对材料表面的化学状态进行精确的表征。拟合过程通常涉及对实验数据与理论模型间的差异进行最小化处理，从而获得材料的组成、化学环境及其电子状态等重要信息。

在本章中，我们将探索XPS峰拟合的基本原理，包括峰形函数的选取、背景扣除的基本方法以及模型参数的调整原则。理解这些基础概念对于深入研究后续章节中涉及的统计学应用、误差分析、模型选择以及实际操作至关重要。

为了更好的理解XPS峰拟合，我们将重点介绍如下几个基础问题：
- 峰形函数的选择及其物理意义；
- 如何通过数学方法对实验数据进行合适的背景扣除；
- 参数调整的优化策略，包括手动与自动优化方法的对比与选择。

# 2. 统计学在XPS峰拟合中的应用

## 2.1 统计学基础概念

### 2.1.1 随机变量与概率分布

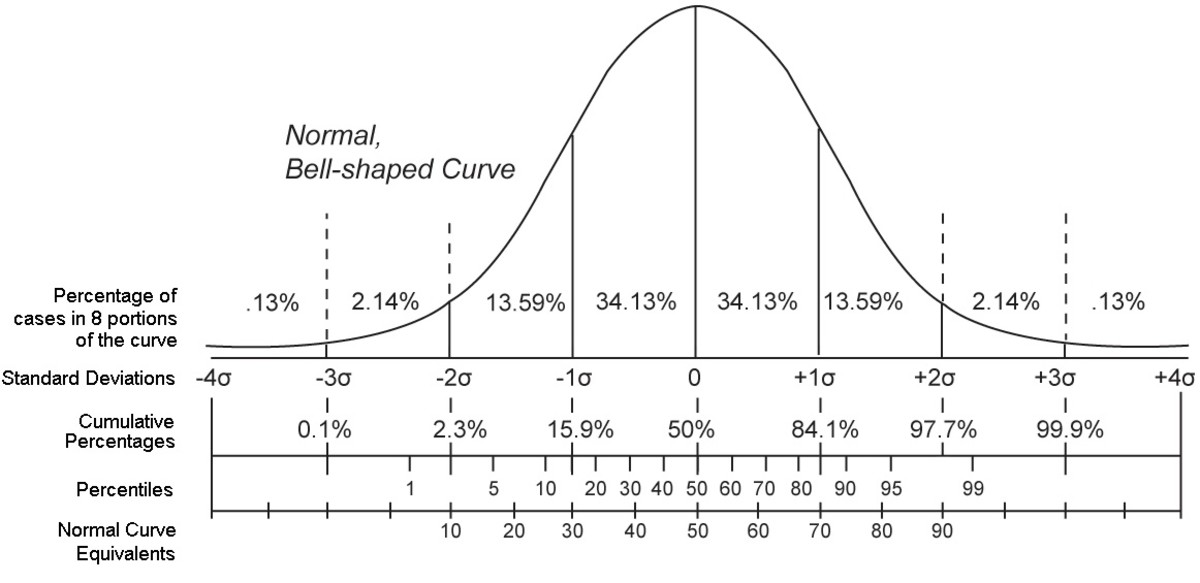
在统计学中，随机变量是一个可以取不同值的变量，其取值结果遵循一定的概率规律。XPS（X射线光电子能谱）峰拟合中，测量得到的光电子强度可以视为随机变量，其强度的波动可以通过概率分布来描述。常见的概率分布包括正态分布（高斯分布）、泊松分布等。

正态分布是最常见的连续概率分布，其概率密度函数具有特定的对称钟形曲线形状，数学表达式如下：

f(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}

其中，$\mu$ 是分布的均值，$\sigma^2$ 是方差，反映了数据的分散程度。在XPS峰拟合中，若测量误差服从正态分布，则可通过最大似然估计等方法来确定峰值位置、峰宽等参数的最优估计。

### 2.1.2 样本、总体与抽样分布

在统计学中，总体指的是研究对象的全部数据，样本则是从总体中抽取的一部分数据。抽样分布是样本统计量（如样本均值）的概率分布。在XPS分析中，总体是指所有可能的测量值，而样本则是我们实际测量到的数据点。

抽样分布的核心在于中心极限定理，该定理指出，不管总体分布为何种形式，只要样本量足够大，样本均值的分布接近正态分布。这意味着，无论XPS峰的形状如何，通过足够数量的测量，我们可以通过拟合一个近似的高斯峰来估计其参数。

### 2.1.3 统计推断

统计推断是从样本数据推断总体参数的过程。在XPS峰拟合中，统计推断包括点估计和区间估计。点估计是对总体参数（如峰位、峰高和峰宽）的单一估计值，而区间估计则给出一个区间，该区间以一定概率包含总体参数的真实值。

## 2.2 XPS峰拟合的误差分析

### 2.2.1 峰位误差与峰宽误差

在XPS峰拟合过程中，峰位误差和峰宽误差是两个关键参数的误差评估指标。峰位误差通常指峰位的估计值与真实值之间的差异，而峰宽误差则是指估计的峰宽与真实峰宽的差异。

对峰位和峰宽误差的分析可以帮助我们评估拟合模型的准确性和可靠性。这些误差可能来源于测量过程中的统计波动、仪器分辨率、背景噪声等。

### 2.2.2 信号噪声与误差传播

在XPS测量中，信号噪声是影响数据质量的主要因素之一。噪声通常来自电子计数的随机性、样品表面的不均匀性以及环境电磁干扰等。

误差传播是指当一个或多个输入量存在误差时，这些误差如何影响最终结果的问题。在XPS峰拟合中，误差传播分析可以帮助我们了解各种来源的误差对峰位、峰宽等参数的估计产生的影响。

### 2.2.3 误差最小化策略

为了减少XPS峰拟合中的误差，可以采用多种策略。常用的策略包括提高测量精度、使用高分辨率的仪器、增加信号的累积时间以减少噪声等。

通过优化拟合模型和算法，例如使用加权最小二乘法来减少不同数据点的权重影响，也能有效地减小误差。此外，合理的数据预处理，比如背景扣除、平滑处理等，也是减少误差的重要手段。

## 2.3 拟合模型选择的统计学方法

### 2.3.1 拟合优度检验

拟合优度检验是统计学中评估拟合模型与实际数据吻合程度的方法。在XPS峰拟合中，常用的拟合优度检验包括残差分析、卡方检验等。

残差是指拟合模型预测值与实际观测值之间的差异。若模型拟合得很好，则残差应接近于零且随机分布。卡方检验则通过比较观测值与理论值之间的差异来评估模型的拟合程度。

### 2.3.2 模型选择标准：AIC与BIC

赤池信息量准则（AIC）和贝叶斯信息量准则（BIC）是评价统计模型复杂性和拟合优度的两种方法。它们基于似然函数并惩罚模型的复杂度，从而帮助选择最简洁且拟合良好的模型。

AIC值越小，表示模型对数据的拟合越好，同时模型复杂度越低。BIC也是类似的，但它的惩罚项更大，因此通常倾向于选择更为简洁的模型。

### 2.3.3 贝叶斯信息准则在模型选择中的应用

贝叶斯信息准则（BIC）是一种基于贝叶斯概率论的方法，用于模型选择。它考虑了模型复杂性和数据拟合程度，定义为：