MATLAB对数插值：解决非线性数据的插值难题，实现数据平滑

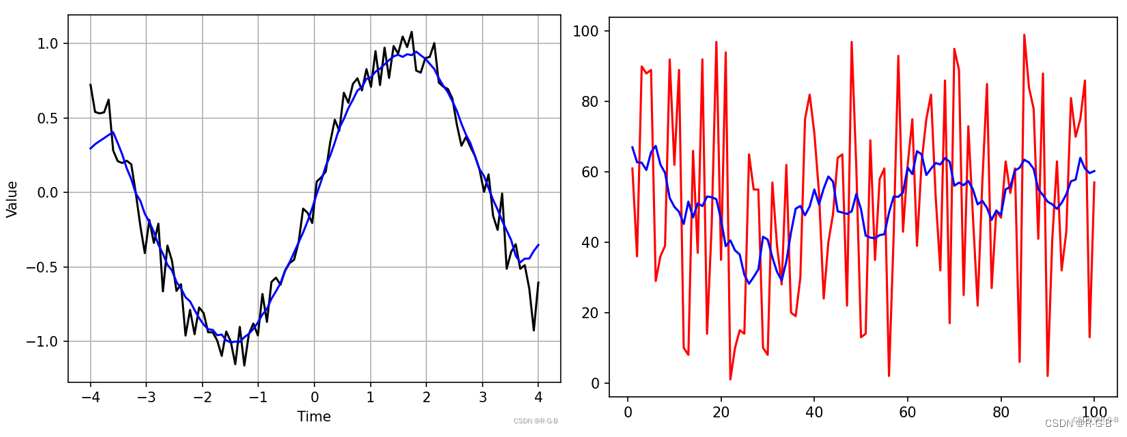
# 1. 对数插值简介**

对数插值是一种插值技术，用于估计给定一组已知数据点之间未知值。它通过对数据进行对数变换，然后使用传统的插值方法（如线性插值或样条插值）来计算未知值。

对数插值特别适用于数据分布不均匀或具有非线性趋势的数据集。通过对数据进行对数变换，可以将数据分布拉平，从而使插值更加准确。

# 2. 对数插值理论**

## 2.1 对数变换的原理

对数变换是一种非线性变换，它将输入数据的范围压缩到一个更窄的范围内。对数变换的公式为：

y = log(x)

其中：

* `x` 是输入数据
* `y` 是对数变换后的数据

对数变换具有以下性质：

* 将正实数映射到实数域
* 将乘法转换为加法
* 将幂转换为乘法

## 2.2 对数插值的数学公式

对数插值是一种基于对数变换的插值方法。它通过对输入数据进行对数变换，然后使用线性插值的方法进行插值，最后再将插值结果进行反对数变换得到最终结果。

对数插值的数学公式为：

y = exp(a + bx)

其中：

* `y` 是插值结果
* `x` 是插值点
* `a` 和 `b` 是通过线性插值得到的系数

**参数说明：**

* `a`：线性插值得到的截距
* `b`：线性插值得到的斜率

**代码块：**

import numpy as np

def log_interpolation(x, y, x_interp):
    """
    对数插值函数

    Args:
        x: 输入数据点的x坐标
        y: 输入数据点的y坐标
        x_interp: 插值点

    Returns:
        插值结果
    """

    # 对输入数据进行对数变换
    log_x = np.log(x)
    log_y = np.log(y)

    # 使用线性插值得到系数a和b
    a, b = np.polyfit(log_x, log_y, 1)

    # 对插值点进行对数变换
    log_x_interp = np.log(x_interp)

    # 计算插值结果
    y_interp = np.exp(a + b * log_x_interp)

    return y_interp

**代码逻辑分析：**

1. `log_x = np.log(x)`：对输入数据点的x坐标进行对数变换。
2. `log_y = np.log(y)`：对输入数据点的y坐标进行对数变换。
3. `a, b = np.polyfit(log_x, log_y, 1)`：使用 `np.polyfit` 函数进行线性插值，得到系数 `a` 和 `b`。
4. `log_x_interp = np.log(x_interp)`：对插值点进行对数变换。
5. `y_interp = np.exp(a + b * log_x_interp)`：计算插值结果，并进行反对数变换。

**流程图：**

graph LR
subgraph 对数插值
    x --> log(x)
    log(x) --> a + bx
    a + bx --> exp(a + bx)
end

# 3. 对数插值