从理论到实践：Radon变换的算法实现指南

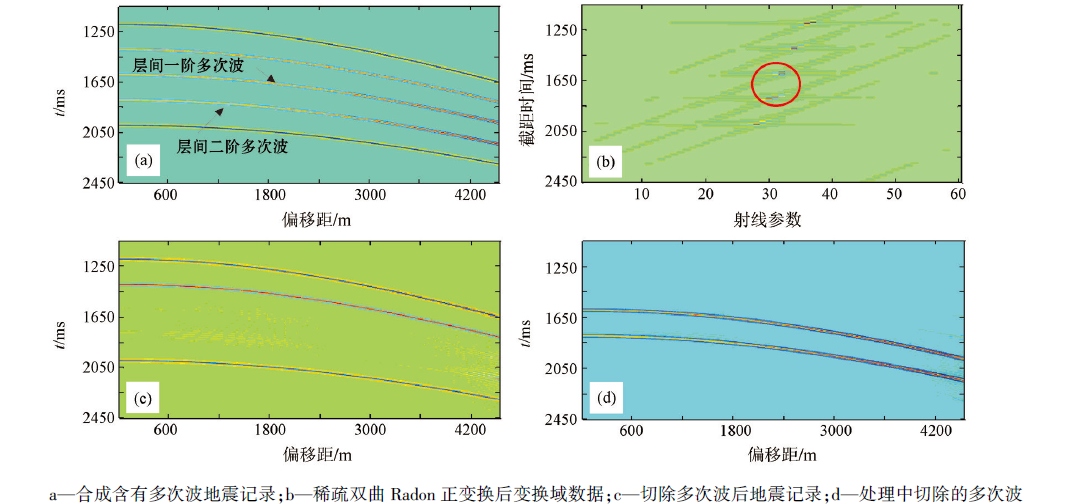
# 1. Radon变换的基础理论**

Radon变换是一种积分变换，它将图像或信号中的直线投影映射到一个新的二维空间中。其数学定义为：

R[f](s, θ) = ∫∫ f(x, y) δ(x cos θ + y sin θ - s) dx dy

其中：

* f(x, y) 是原始图像或信号
* s 是投影线到原点的距离
* θ 是投影线的角度
* δ(x) 是狄拉克δ函数

Radon变换的逆变换，即反Radon变换，可以将投影数据恢复为原始图像或信号。反Radon变换的数学定义为：

f(x, y) = (1/2π) ∫0^π ∫-∞^∞ R[f](s, θ) |x cos θ + y sin θ - s| ds dθ

Radon变换在图像处理、信号处理和计算机视觉等领域有着广泛的应用。它可以用于图像重建、去噪、增强和特征提取等任务。

# 2. Radon变换的算法实现

### 2.1 离散Radon变换算法

离散Radon变换（DRT）将连续Radon变换离散化，使其可以在计算机上进行计算。DRT的两种主要算法是滤波反投影算法和加权反投影算法。

#### 2.1.1 滤波反投影算法

滤波反投影算法（FBP）是DRT中最常用的算法。其步骤如下：

1. **滤波：**将投影数据沿每个角度方向进行滤波，以抑制噪声和伪影。常用的滤波器包括拉姆拉克滤波器和谢帕德滤波器。
2. **反投影：**将滤波后的投影数据沿每个角度反投影回图像空间。
3. **求和：**将所有角度的反投影结果相加，得到重建的图像。

import numpy as np
from scipy.ndimage import convolve

def radon_fbp(projections, angles, filter):
    """
    滤波反投影算法进行Radon变换

    参数：
        projections: 投影数据，形状为 (角度数量, 投影长度)
        angles: 投影角度，形状为 (角度数量,)
        filter: 滤波器，形状为 (滤波器长度,)

    返回：
        重建的图像，形状为 (图像大小, 图像大小)
    """

    # 滤波
    filtered_projections = np.zeros_like(projections)
    for i in range(projections.shape[0]):
        filtered_projections[i] = convolve(projections[i], filter)

    # 反投影
    reconstructed_image = np.zeros((projections.shape[1], projections.shape[1]))
    for i in range(projections.shape[0]):
        reconstructed_image += filtered_projections[i] * np.sin(angles[i])

    return reconstructed_image

**逻辑分析：**

* `radon_fbp`函数接受投影数据、投影角度和滤波器作为输入。
* 首先，对投影数据沿每个角度方向进行滤波。
* 然后，将滤波后的投影数据沿每个角度反投影回图像空间。
* 最后，将所有角度的反投影结果相加，得到重建的图像。

#### 2.1.2 加权反投影算法

加权反投影算法（WBP）与FBP类似，但它使用权重函数来补偿反投影过程中引入的伪影。权重函数通常是拉姆拉克滤波器的倒数。

import numpy as np
from scipy.ndimage import convolve

def radon_wbp(projections, angles, filter):
    """
    加权反投影算法进行Radon变换

    参数：
        projections: 投影数据，形状为 (角度数量, 投影长度)
        angles: 投影角度，形状为 (角度数量,)
        filter: 滤波器，形状为 (滤波器长度,)

    返回：
        重建的图像，形状为 (图像大小, 图像大小)
    """

    # 滤波
    filtered_projections = np.zeros_like(projections)
    for i in range(projections.shape[