MATLAB反三角函数的精度陷阱：避免计算误区，提升代码可靠性

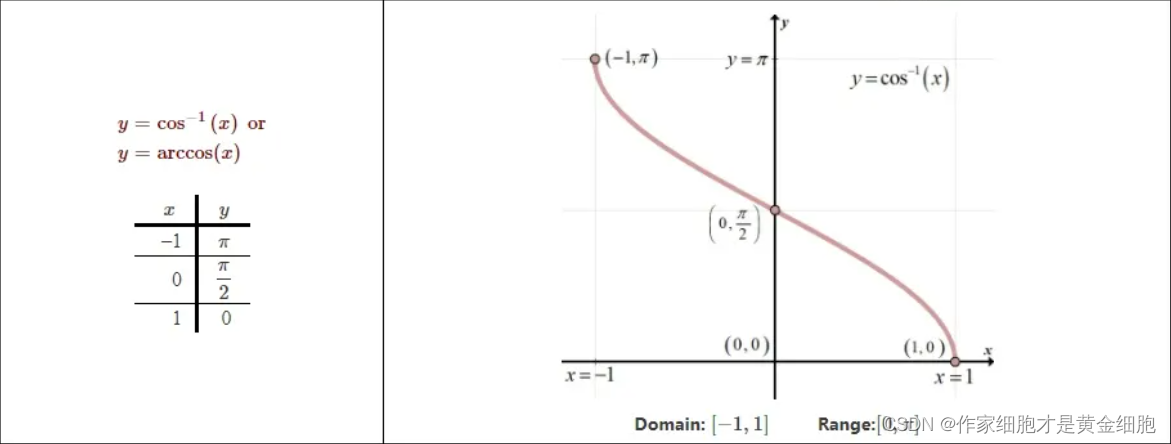
# 1. MATLAB反三角函数概述

反三角函数，也称为反圆函数，是一类将角度作为输入并返回其对应的三角函数值的函数。MATLAB提供了丰富的反三角函数，包括`asin`、`acos`和`atan`，用于计算正弦、余弦和正切的反函数。这些函数在科学计算、工程和数据分析中广泛应用。

反三角函数的计算涉及到复杂且精细的数学运算。在MATLAB中，反三角函数的精度受限于计算机的有限精度计算能力。因此，在使用反三角函数时，需要充分了解其精度陷阱，并采取适当的措施来避免潜在的误差。

# 2. 反三角函数的精度陷阱

反三角函数在计算中广泛应用，但由于其固有的精度限制，可能导致意想不到的误差。本章节将深入分析反三角函数的精度陷阱，探讨误差的成因、类型和影响，并提供避免这些陷阱的实践技巧。

### 2.1 精度误差的成因分析

#### 2.1.1 有限精度计算

计算机以有限精度表示数字，这意味着数值只能近似表示为有限位数的二进制小数。当进行反三角函数计算时，输入参数和计算结果都受到有限精度的影响，可能导致舍入误差。

#### 2.1.2 输入参数范围的影响

反三角函数的精度也受输入参数范围的影响。对于某些输入值，反三角函数的导数接近于零，这会放大舍入误差。例如，当输入参数接近于 π/2 时，反正弦函数的导数接近于零，导致计算结果的精度下降。

### 2.2 常见误差类型和影响

#### 2.2.1 角度范围限制

反三角函数只定义在特定角度范围内，超出该范围的输入值会产生错误或不准确的结果。例如，反正弦函数只定义在 [-π/2, π/2] 范围内，超出该范围的输入值会返回 NaN（非数字）。

#### 2.2.2 特殊值处理

反三角函数在处理无穷大、负无穷大和 NaN 等特殊值时，可能会产生不直观的结果。例如，反正切函数在输入为无穷大时返回 π/2，而输入为负无穷大时返回 -π/2。

# 3. 避免精度陷阱的实践技巧

### 3.1 选择合适的精度模式

**3.1.1 双精度计算**

MATLAB 中的双精度计算使用 64 位浮点数，提供比单精度计算更高的精度。对于反三角函数计算，双精度计算可以有效减少精度误差，特别是在输入参数范围较大的情况下。

% 双精度计算
x = 1e10;
asin_double = asin(x);

% 单精度计算
x_single = single(x);
asin_single = asin(x_single);

% 比较结果
disp(['双精度结果：', num2str(asin_double)]);
disp(['单精度结果：', num2str(asin_single)]);

**代码逻辑分析：**

* `asin_double` 和 `asin_single` 分别存储双精度和单精度计算的反三角函数值。
* `num2str` 函数将数字转换为字符串，便于显示。

**3.1.2 符号计算**

符号计算使用符号变量和表达式，而不是浮点数，进行计算。这可以消除舍入误差，从而获得精确的结果。MATLAB 中的 `syms` 函数可以创建符号变量，`vpa` 函数可以进行符号计算。

% 符号计算
syms x;
asin_symbolic = asin(x);

% 将符号结果转换为双精度浮点数
asin_double = double(asin_symbolic);

% 比较结果
disp(['符号计算结果：', char(asin_symbolic)]);
disp(['双精度浮点数结果：', num2str(asin_double)]);

**代码逻辑分析：**

* `syms x` 创建符号变量 `x`。
* `asin_symbolic` 存储符号计算的反三角函数结果。
* `double(asin_symbolic)` 将符号结果转换为双精度浮点数。
* `ch