量子效应模拟基础与应用
发布时间: 2024-12-15 10:33:09 阅读量: 2 订阅数: 4 


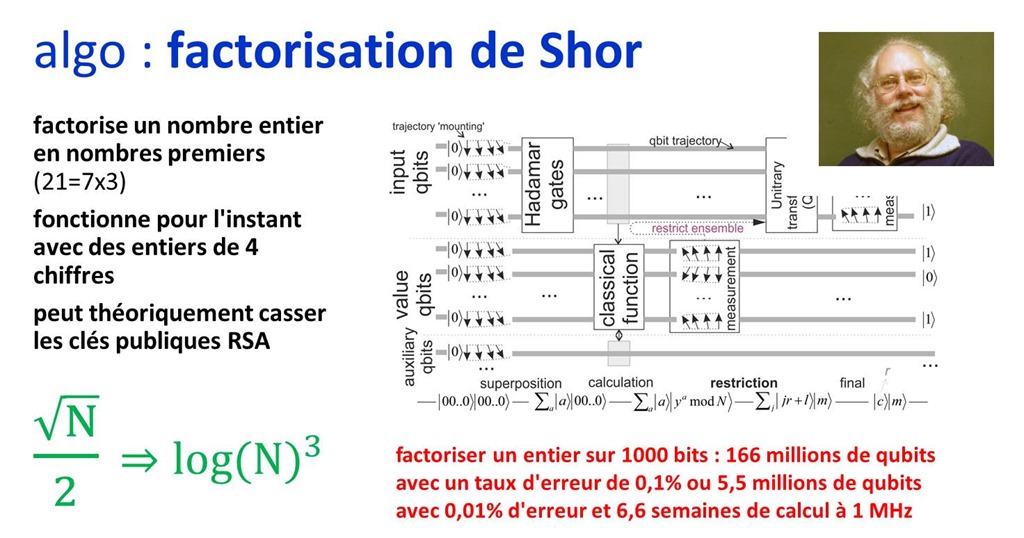
量子计算加速装备设计与模拟.pptx
参考资源链接:[Silvaco TCAD器件仿真教程:材料与物理模型设定](https://wenku.csdn.net/doc/6moyf21a6v?spm=1055.2635.3001.10343)
# 1. 量子效应模拟基础
## 量子效应模拟的起源与重要性
量子效应模拟是研究微观世界的重要工具,它允许科学家和工程师在计算机上再现量子系统的动态行为。模拟量子系统要求我们理解量子力学的基本原则,包括波粒二象性、叠加原理和纠缠现象。这些原则为量子计算、量子通信和量子信息处理等前沿科学领域提供了理论基础。
量子效应模拟不仅对于基本科学研究至关重要,它在材料科学、药物发现和纳米技术等领域也有广泛应用。通过模拟,研究人员能够在不实际创建材料或设备的情况下预测其属性和性能。本章将探讨量子模拟的基本概念和方法,为读者进入量子模拟的世界打下坚实的基础。
# 2. 量子力学理论与模拟方法
## 2.1 量子力学基本原理
量子力学是研究物质世界最基本层面的物理理论,它的基本原理为我们提供了一套理解和模拟量子现象的框架。
### 2.1.1 波函数与薛定谔方程
波函数是量子力学的核心概念之一,它描述了粒子在量子态中的概率分布。薛定谔方程是描述量子系统状态随时间演化的基本方程。在时间独立的情况下,我们可以得到时间无关的薛定谔方程:
```
iħ∂ψ/∂t = Ĥψ
```
其中 `i` 是虚数单位,`ħ` 是约化普朗克常数,`ψ` 是波函数,而 `индивидуальн` 是哈密顿算符。在给定系统的边界条件和初始状态后,求解薛定谔方程可以得到系统的能量本征值和对应的本征态。
```python
import numpy as np
import scipy.linalg as la
# 假设我们有一个简单的一维势能井问题
def hamiltonian_operator(V, dx):
tridiagonal_matrix = np.diag(np.ones(len(V)-1), k=1) + np.diag(np.ones(len(V)-1), k=-1)
diagonal_matrix = np.diag(V)
return tridiagonal_matrix + diagonal_matrix
def solve_schrodinger(V, dx):
H = hamiltonian_operator(V, dx)
eigenvalues, eigenvectors = la.eigh(H)
return eigenvalues, eigenvectors
# 示例势能井
V = np.zeros(100)
V[40:60] = 1 # 在40到60位置创建势能井
eigenvalues, eigenvectors = solve_schrodinger(V, 0.1)
```
### 2.1.2 测量与不确定性原理
海森堡不确定性原理说明了粒子的位置和动量不可能同时被精确测量,这反映了量子系统的本质波动性。不确定性原理可以用公式表示为:
```
Δx * Δp >= ħ/2
```
其中 `Δx` 是位置的标准差,`Δp` 是动量的标准差。此原理意味着在量子尺度上,我们无法精确预知粒子的未来行为,只能计算出发生各种结果的概率。
## 2.2 数值模拟方法
在量子模拟中,数值方法提供了一种强大的工具,可以帮助我们解决那些无法找到解析解的复杂问题。
### 2.2.1 有限差分法与矩阵对角化
有限差分法是将连续的空间划分为离散的点,并利用差分近似来代替微分方程中的导数。这种方法通常用于求解偏微分方程,如时间无关的薛定谔方程。矩阵对角化是一种数学技术,用于找到矩阵的本征值和本征向量。这对于求解量子系统的能量本征态和计算物理量非常有用。
```python
# 使用有限差分法近似求解二维薛定谔方程
def finite_difference_schrodinger_2d(V, dx, dy):
N = int((1/dx)**2)
H = np.zeros((N, N))
# 有限差分法的实现细节
# ...
eigenvalues, eigenvectors = la.eigsh(H, k=10) # 近似求解本征值问题
return eigenvalues, eigenvectors
```
### 2.2.2 蒙特卡洛方法与随机模拟
蒙特卡洛方法是一种基于随机抽样的计算技术,用于模拟粒子系统的行为。在量子模拟中,它通常被用来估计量子态的某些物理属性。这种方法在高维问题中特别有用,因为它不需要显式地解决薛定谔方程。
```python
import random
# 简单的蒙特卡洛方法示例
def monte_carlo_simulation(number_of_samples):
results = []
for _ in range(number_of_samples):
random_value = random.random()
results.append(random_value)
return sum(results)/number_of_samples
```
### 2.2.3 时间演化算符与时间分裂技术
时间演化算符描述了量子态随时间的变化。时间分裂技术是一种将时间演化算符分成几个简单的操作,并分别计算每个操作对量子态的影响的方法。这在模拟动态系统时非常有用。
```python
# 时间分裂技术的示例
def time_splitting_operator(H1, H2, dt):
# 假设 H1 和 H2 是时间分裂中的两个算符
U1 = np.exp(-1j * H1 * dt / 2)
U2 = np.exp(-1j * H2 * dt)
U = U1 @ U2
return U
```
## 2.3 模拟软件与工具
有许多软件和工具可以帮助我们进行量子模拟,它们各有特色,适合不同类型的模拟任务。
### 2.3.1 常用量子模拟软件介绍
一些常用的量子模拟软件包括Qiskit、Cirq和Qiskit。这些工具提供了创建量子电路、执行量子算法以及模拟量子计算机行为的接口。
### 2.3.2 软件的选择与配置
选择合适的模拟软件需要考虑任务的类型、模拟的规模以及熟悉度。例如,对于初学者,可能会从Qiskit开始,因为它有丰富的文档和教程。而对于更高级的研究,可能需要使用Cirq,它提供了更底层的操作。
```python
# 使用Qiskit的示例代码
from qiskit import QuantumCircuit, Aer, execute
simulator = Aer.get_backend('qasm_simulator')
circuit = QuantumCircuit(2, 2)
circuit.h(0)
circuit.cx(0, 1)
circuit.measure([0,1], [0,1])
job = execute(circuit, simulator, shots=1024)
result = job.result()
counts = result.get_counts(circuit)
```
量子力学理论与模拟方法是进行量子模拟不可或缺的基础。在接下来的章节中,我们将深入实践操作,并探索量子模拟在材料科学和化学反应中的应用。随着量子技术的不断发展,这些方法和工具也在不断演化,为研究者提供了更多可能。
# 3. 量子效应模拟实践操作
在理解了量子效应模拟的理论基础和数值模拟方法之后,我们来到了实践操作的环节。在这一章节中,我们将以两个角度来探索量子效应模拟的实际应用,分别是理想量子系统模拟和非理想条件下的模拟。此外,还会探讨杂质和缺陷如何影响量子系统的模拟结果。
## 3.1 理想量子系统模拟
理想量子系统模拟主要关注于在完美控制条件下的量子行为。这里我们将分析如何使用模
0
0






