MATLAB求平均值的正确姿势：掌握函数和循环，高效处理数据

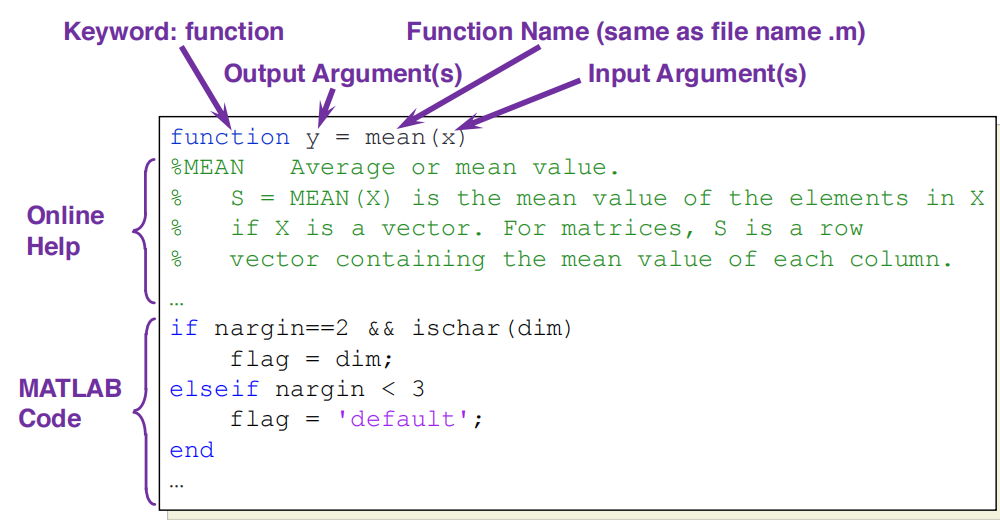
# 1. MATLAB求平均值的理论基础

平均值是统计学中常用的一个概念，表示一组数据的中心趋势。在MATLAB中，求平均值有以下几种方法：

- 使用mean()函数：mean()函数是MATLAB中专门用于求平均值的函数，它可以对向量、矩阵或多维数组进行求平均值操作。
- 使用sum()和numel()函数：sum()函数可以对数组中的元素求和，numel()函数可以返回数组中的元素个数。通过这两个函数的配合，也可以实现求平均值的功能。

# 2. MATLAB求平均值的函数实现

在MATLAB中，求平均值可以通过多种函数实现，其中最常用的函数是`mean()`函数。

### 2.1 mean()函数的用法和特点

`mean()`函数用于计算输入数组中所有元素的算术平均值。其语法格式如下：

mean(X)

其中：

* `X`：输入数组。

`mean()`函数的输出是一个标量，表示输入数组中所有元素的平均值。

**特点：**

* `mean()`函数可以处理任意维度的数组。
* `mean()`函数对NaN（非数字）值进行忽略，不会影响平均值的计算。
* `mean()`函数可以沿指定维度计算平均值。

**示例：**

% 计算一维数组的平均值
x = [1, 2, 3, 4, 5];
avg_x = mean(x)

% 计算二维数组的平均值
A = [1, 2, 3; 4, 5, 6; 7, 8, 9];
avg_A = mean(A)

% 沿指定维度计算平均值
avg_A_row = mean(A, 1) % 按行计算平均值
avg_A_col = mean(A, 2) % 按列计算平均值

### 2.2 sum()和numel()函数的配合应用

除了`mean()`函数，还可以使用`sum()`和`numel()`函数配合计算平均值。`sum()`函数用于计算数组中所有元素的和，`numel()`函数用于计算数组中元素的个数。

**语法格式：**

avg = sum(X) / numel(X)

其中：

* `X`：输入数组。

**特点：**

* 这种方法可以处理任意维度的数组。
* 这种方法对NaN值进行忽略，不会影响平均值的计算。

**示例：**

% 计算一维数组的平均值
x = [1, 2, 3, 4, 5];
avg_x = sum(x) / numel(x)

% 计算二维数组的平均值
A = [1, 2, 3; 4, 5, 6; 7, 8, 9];
avg_A = sum(A) / numel(A)

**代码块：**

% 计算一维数组的平均值
x = [1, 2, 3, 4, 5];
avg_x = sum(x) / numel(x);

% 计算二维数组的平均值
A = [1, 2, 3; 4, 5, 6; 7, 8, 9];
avg_A = sum(A) / numel(A);

% 打印结果
disp(['平均值（一维数组）：', num2str(avg_x)]);
disp(['平均值（二维数组）：', num2str(avg_A)]);

**逻辑分析：**

* 对于一维数组`x`，使用`sum()`函数计算所有元素的和，再除以`numel()`函数计算的元素个数，得到平均值`avg_x`。
* 对于二维数组`A`，使用`sum()`函数计算所有元素的和，再除以`numel()`函数计算的元素个数，得到平均值`avg_A`。

# 3. MATLAB求平均值的循环实现

### 3.1 for循环的遍历求和

for循环是一种迭代语句，它允许我们遍历数组中的每个元素并执行特定的操作。在求平均值的情况下，我们可以使用for循环来遍历数组中的所有元素，将其求和，然后将总和除以元素总数。

% 创建一个数组
data = [1, 2, 3, 4, 5];

% 初始化总和变量
sum = 0;

% 使用for循环遍历数组
for i = 1:length(data)
    % 将每个元素添加到总和中
    sum = sum + data(i);
end

% 计算平均值
mean_value = sum / length(data);

% 输出平均值
disp(['平均值：', num2str(mean_value)]);

**代码逻辑逐行解读：**

1. 创建一个数组`data`，其中包含要计算平均值的值。
2. 初始化一个变量`sum`来存储元素的总和。
3. 使用`for`循环遍历数组中的每个元素。
4. 在每次迭代中，将当前元素添加到`sum`中。
5. 计算平均值，方法是将`sum`除以数组的长度。
6. 输出平均值。

### 3.2 while循环的条件求和

while循环是一种迭代语句，它允许我们重复执行一个代码块，直到满足特定的条件。在求平均值的情况下，我们可以使用while循环来遍历数组中的所有元素，将其求和，然后将总和除以元素总数。

% 创建一个数组
data = [1, 2, 3, 4, 5];

% 初始化总和变量
sum = 0;

% 初始化元素计数器
count = 0;

% 使用while循环遍历数组
while count < length(data)
    % 将当前元素添加到总和中
    sum = sum + data(count + 1);
    % 递增元素计数器
    count = count + 1;
end

% 计算平均值
mean_value = sum / length(data);

% 输出平均值
disp(['平均值：', num2str(mean_value)]);

**代码逻辑逐行解读：**

1. 创建一个数组`data`，其中包含要计算平均值的值。
2. 初始化一个变量`sum`来存储元素的总和。
3. 初始化一个变量`count`来跟踪已遍历的元素数。
4. 使用`while`循环遍历数组中的每个元素，直到`count`达到数组长度。
5. 在每次迭代中，将当前元素添加到`sum`中。
6. 递增`count`以跟踪已遍历的元素数。
7. 计算平均值，方法是将`sum`除以数组的长度。
8. 输出平均值。

# 4. MATLAB求平均值的进阶应用

### 4.1 多维数组的平均值计算

在实际应用中，经常会遇到多维数组的平均值计算问题。MATLAB提供了多种方法来计算多维数组的平均值。

**mean()函数的应用**

mean()函数可以计算多维数组沿指定维度的平均值。例如，对于一个三维数组`A`，沿第一维度计算平均值：

B = mean(A, 1);

此时，`B`是一个二维数组，其每一行是`A`沿第一维度（行）的平均值。

**reshape()函数的配合应用**

reshape()函数可以将多维数组重新排列为一维数组，然后使用mean()函数计算平均值。例如，对于一个三维数组`A`，沿所有维度计算平均值：

B = mean(reshape(A, [], 1));

此时，`B`是一个标量，表示`A`的平均值。

### 4.2 加权平均值的计算

加权平均值是根据每个元素的权重计算的平均值。MATLAB提供了`weightedmean()`函数来计算加权平均值。

**weightedmean()函数的用法**

weightedmean()函数的语法为：

weightedmean(X, W)

其中：

* `X`：输入数据，可以是一维或多维数组。
* `W`：权重向量，与`X`具有相同的大小。

**示例**

计算一组数据的加权平均值：

data = [1, 2, 3, 4, 5];
weights = [0.2, 0.3, 0.1, 0.2, 0.2];
weighted_avg = weightedmean(data, weights);

此时，`weighted_avg`的值为2.6。

**扩展**

* **权重归一化：**在计算加权平均值之前，通常需要对权重进行归一化，以确保权重之和为1。
* **加权标准差：**MATLAB提供了`weightedstd()`函数来计算加权标准差。

# 5. MATLAB 求平均值的实践案例

### 5.1 数据分析中的平均值应用

**案例：计算一组数据的平均值**

% 数据准备
data = [2, 4, 6, 8, 10];

% 使用 mean() 函数计算平均值
avg = mean(data);

% 输出结果
fprintf('数据平均值：%.2f\n', avg);

### 5.2 图像处理中的平均值滤波

**案例：使用平均值滤波器平滑图像**

% 读取图像
img = imread('image.jpg');

% 定义滤波器大小
filter_size = 3;

% 创建平均值滤波器
avg_filter = ones(filter_size) / (filter_size^2);

% 应用平均值滤波
filtered_img = imfilter(img, avg_filter);

% 显示原图和滤波后的图像
figure;
subplot(1, 2, 1);
imshow(img);
title('原图');
subplot(1, 2, 2);
imshow(filtered_img);
title('滤波后图像');