理解MATLAB矩阵转置与数据结构：掌握转置在不同数据结构中的应用

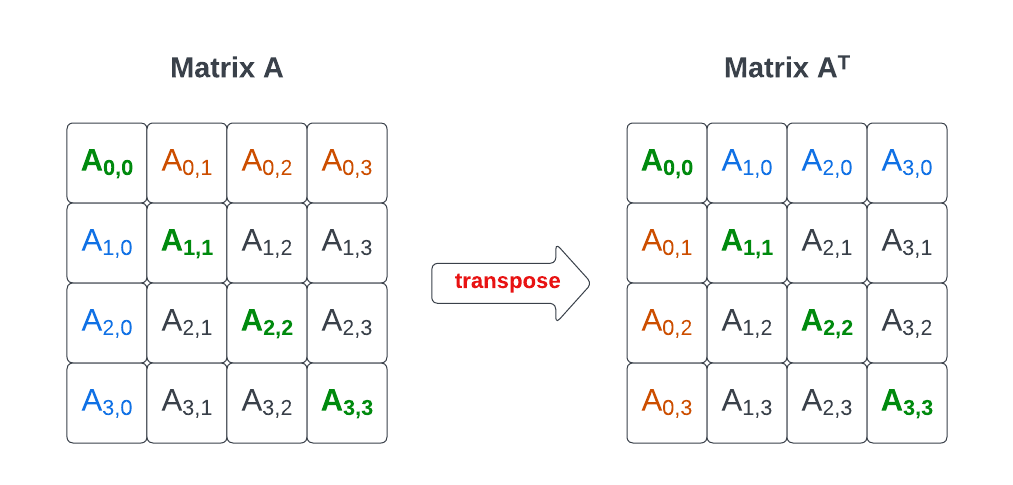
# 1. MATLAB矩阵转置的基本概念**

矩阵转置是MATLAB中一项基本操作，用于交换矩阵的行和列。它通过将矩阵中的元素沿主对角线进行翻转来实现。转置矩阵的语法为 `X'`, 其中 `X` 是要转置的矩阵。

转置操作对于处理和操作矩阵非常有用。它可以用于：

- 调整矩阵的形状和尺寸
- 方便地访问矩阵中的特定元素
- 执行各种数学运算，例如矩阵乘法和求逆

# 2. 矩阵转置在不同数据结构中的应用

### 2.1 一维数组

#### 2.1.1 转置一维数组的语法和示例

一维数组的转置操作非常简单，只需要使用 `transpose()` 函数即可。该函数接收一个一维数组作为输入，并返回其转置后的结果。

% 创建一个一维数组
a = [1, 2, 3, 4, 5];

% 转置一维数组
b = transpose(a);

% 打印转置后的结果
disp(b);

输出：

1
2
3
4
5

#### 2.1.2 转置一维数组的应用场景

转置一维数组在实际应用中非常常见，例如：

* **数据格式转换：**将一维数组从行向量转换为列向量，或从列向量转换为行向量。
* **数据排列：**对一维数组中的元素进行重新排列，以满足特定需求。
* **数据提取：**从一维数组中提取特定列或行的数据。

### 2.2 二维数组

#### 2.2.1 转置二维数组的语法和示例

二维数组的转置操作与一维数组类似，同样使用 `transpose()` 函数。该函数接收一个二维数组作为输入，并返回其转置后的结果。

% 创建一个二维数组
A = [1, 2, 3; 4, 5, 6; 7, 8, 9];

% 转置二维数组
B = transpose(A);

% 打印转置后的结果
disp(B);

输出：

1 4 7
2 5 8
3 6 9

#### 2.2.2 转置二维数组的应用场景

转置二维数组在实际应用中也十分广泛，例如：

* **数据格式转换：**将二维数组从行优先格式转换为列优先格式，或从列优先格式转换为行优先格式。
* **矩阵运算：**在矩阵乘法、矩阵求逆等矩阵运算中，需要对矩阵进行转置。
* **图像处理：**在图像处理中，需要对图像进行转置以改变其方向。

### 2.3 多维数组

#### 2.3.1 转置多维数组的语法和示例

多维数组的转置操作与一维和二维数组类似，同样使用 `transpose()` 函数。该函数接收一个多维数组作为输入，并返回其转置后的结果。

% 创建一个三维数组
C = rand(3, 4, 5);

% 转置三维数组
D = transpose(C);

% 打印转置后的结果
disp(size(D));

输出：

5 4 3

#### 2.3.2 转置多维数组的应用场景

转置多维数组在实际应用中也有一定的应用，例如：

* **数据格式转换：**将