数据结构在EDID256位设计中的决定性作用：存储与处理的高效艺术


# 摘要
数据结构是计算机科学的基础，直接影响到EDID（Extended Display Identification Data）设计的效率和性能。本文全面介绍了数据结构与EDID设计的关系，强调了核心数据结构的理论基础及其在EDID设计中的实际应用。特别关注了树形结构、图结构和散列表在EDID索引、路由优化和数据检索中的关键作用。同时，探讨了数据结构在存储优化、实时处理和安全机制中的创新应用。通过案例分析，本文提供了实践应用指导，并展望了数据结构在未来EDID设计中的发展趋势。本文旨在为EDID开发者提供深入的理论知识和实践工具，以提高EDID系统的性能和安全性。

# 关键字
数据结构；EDID设计；树形结构；图结构；散列表；实时数据处理；安全性

参考资源链接：[解析256字节EDID设计规范与详细解读](https://wenku.csdn.net/doc/jykq2hqbb1?spm=1055.2635.3001.10343)
# 1. 数据结构与EDID256位设计概述

随着信息技术的快速发展，数据结构作为计算机科学的核心基础之一，它对于数据的存储、处理和检索效率起着至关重要的作用。尤其在设计和实现EDID（Enhanced Data Identification）系统的256位数据结构时，对数据结构的理解与应用变得尤为关键。EDID系统是一种先进的数据管理解决方案，它需要在保证数据一致性和完整性的同时，提供高速的数据检索和处理能力。本章将对数据结构与EDID设计的关系进行概述，并介绍数据结构设计的基本原则和目标，为后续章节中对数据结构在EDID256位设计中应用的深入探讨打下坚实的基础。

# 2. 核心数据结构的理论基础

## 2.1 数据结构的分类与特性

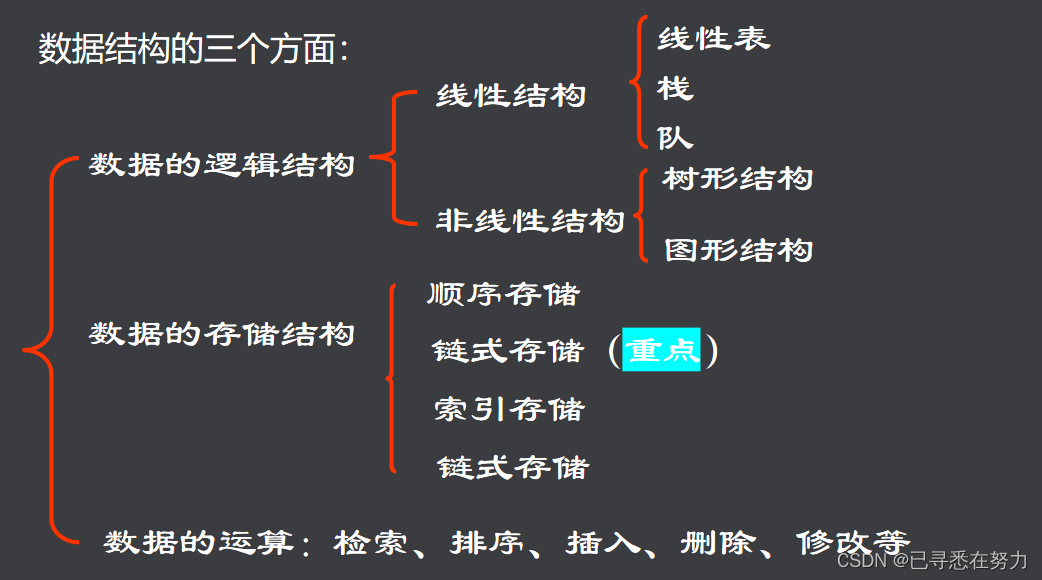
### 2.1.1 线性结构和非线性结构

数据结构是组织和存储数据的一种方式，以便可以高效地访问和修改。在数据结构领域，我们可以将其分为两大类：线性结构和非线性结构。理解这两种结构的特性对于设计高效的数据管理系统至关重要。

**线性结构**是指数据元素之间存在一对一的关系。例如，在数组和链表中，每个元素（除了第一个和最后一个）都有一个前驱和一个后继元素。线性结构易于实现和理解，但在处理大量数据时可能会引起性能问题。典型的数据结构如栈、队列、列表和数组都属于线性结构。

**非线性结构**指的是数据元素之间存在一对多或多对多的关系。最常见的非线性结构包括树和图。在这种结构中，数据元素之间的连接更加复杂，这使得它们在表达复杂数据关系时更加灵活。例如，树结构允许快速查找、插入和删除操作，而图结构则在表达网络和关系数据库方面更为合适。

### 2.1.2 数据结构的抽象数据类型（ADT）

抽象数据类型（ADT）提供了一种定义数据结构的高级视图，它与数据结构的具体实现无关。通过ADT，我们可以专注于数据结构能够执行的操作，而不必关心这些操作是如何实现的。这种抽象有助于简化复杂的数据结构设计和使用。

ADT的基本组成包括数据的表示方式以及一组操作。这些操作定义了数据结构可以进行的合法操作集合。常见的ADT包括列表、栈、队列、集合、映射和字典等。例如，栈的ADT通常包含push、pop和peek等操作，而映射的ADT则包括put、get和remove等操作。

通过ADT，开发者可以编写与具体数据结构解耦的通用代码，使得代码更加模块化和易于维护。同时，这也允许开发者在不影响程序其他部分的情况下，更换不同的数据结构实现。

# 示例：栈的抽象数据类型实现
class Stack:
    def __init__(self):
        self.items = []

    def is_empty(self):
        return len(self.items) == 0

    def push(self, item):
        self.items.append(item)

    def pop(self):
        if not self.is_empty():
            return self.items.pop()
        raise IndexError("pop from an empty stack")
    def peek(self):
        if not self.is_empty():
            return self.items[-1]
        raise IndexError("peek from an empty stack")

在上述Python示例中，`Stack`类定义了一个简单的栈ADT，包括初始化、检查是否为空、添加元素到栈顶、移除栈顶元素以及查看栈顶元素等操作。

## 2.2 数据结构在存储中的角色

### 2.2.1 存储结构的选择标准

选择合适的数据存储结构对于任何系统来说都是一个关键的决策点，因为不同的数据结构直接影响到数据的存储效率和访问速度。存储结构的选择通常基于数据的使用模式和操作需求。

**数据使用模式**是指数据是如何被访问和修改的，以及这种访问和修改的频率如何。例如，如果一个应用需要频繁地在数据集的末尾添加新元素，那么使用队列或链表可能比使用数组更为高效。

**操作需求**包括所需执行的各种操作类型，如插入、删除、查找和更新等。数据结构的设计应该使得最频繁的操作尽可能高效。例如，如果一个应用主要执行查找操作，那么散列表可能是最佳选择，因为它提供了接近常数时间的查找效率。

### 2.2.2 时间复杂度与空间复杂度的权衡

在选择数据存储结构时，必须在时间复杂度和空间复杂度之间找到一个平衡点。时间复杂度指的是执行操作所需的步骤数量，而空间复杂度指的是所需存储空间的大小。

例如，数组提供了快速的随机访问能力，但它在插入和删除操作时可能需要移动大量的元素，这导致较高的时间复杂度。相比之下，链表在插入和删除时非常高效，但查找特定元素时需要遍历整个链表，这导致较高的时间复杂度。

在许多情况下，开发者需要根据具体应用需求，在快速访问和插入/删除操作之间做出选择。一个常见的解决方案是使用如平衡二叉搜索树或哈希表这样的高级数据结构，这些结构尝试在不同操作之间提供更好的折衷。

graph TD;
    A[存储结构选择] --> B[数组]
    A --> C[链表]
    A --> D[散列表]
    A --> E[树]
    B --> F[快速随机访问]
    B --> G[高插入删除时间复杂度]
    C --> H[快速插入删除]
    C --> I[慢速随机访问]
    D --> J[常数时间复杂度的查找]
    E --> K[有序数据高效操作]

在上述mermaid流程图中，展示了存储结构选择的决策树，帮助开发者根据不同的使用模式和操作需求来选择最合适的存储结构。

## 2.3 数据结构在处理中的效率

### 2.3.1 常见操作的时间复杂度分析

时间复杂度是衡量算法性能的一个重要指标，尤其在处理大量数据时。在数据结构的上下文中，常见的操作包括插入、删除、查找和遍历等。不同数据结构对这些操作的时间复杂度影响很大。

例如，在数组中查找特定元素的时间复杂度为O(n)，因为可能需要遍历整个数组。相比之下，在二叉搜索树中，查找特定元素的时间复杂度为O(log n)，这得益于树的层级结构。散列表通常提供接近O(1)的查找时间，但这也依赖于散列函数的质量和负载因子。

### 2.3.2 结构操作对整体性能的影响

结构操作不仅影响单个操作的性能，还可能对整体系统的性能产生重大影响。例如，在一个数据库系统中，如果底层存储结构不能快速处理查询请求，那么整体响应时间将会增加。同样，在一个网络系统中，如果路由表结构不能迅速更新和查找路由信息，那么网络效率将受到影响。

此外，数据结构的选择还会影响到系统的可扩展性。例如，在设计一个大规模分布式系统时，选择适合分布式环境的数据结构（如一致性哈希）可以有效地提升系统的性能和可靠性。

graph LR;
    A[数据操作] --> B[查找]
    A --> C[插入]
    A --> D[删除]
    B --> E[时间复杂度分析]
    C --> E
    D --> E
    E --> F[影响系统性能]
    F --> G[单个操作性能]
    F --> H[整体系统性能]
    F --> I[系统可扩展性]

上述mermaid流程图展示了数据操作如何通过时间复杂度分析影响系统的各个方面，从单个操作到整个系统的性能和可扩展性。

以上内容介绍了核心数据结构的理论基础，包括线性与非线性结构的区别，抽象数据类型的概念，以及存储结构选择时的标准和性能权衡。通过对比不同数据结构的操作效率和对系统性能的潜在影响，我们可以为特定的应用选择最合适的