【Python多返回值解包】：掌握元组与解包技巧

# 1. Python多返回值的基础概念

## 1.1 多返回值的定义和用途
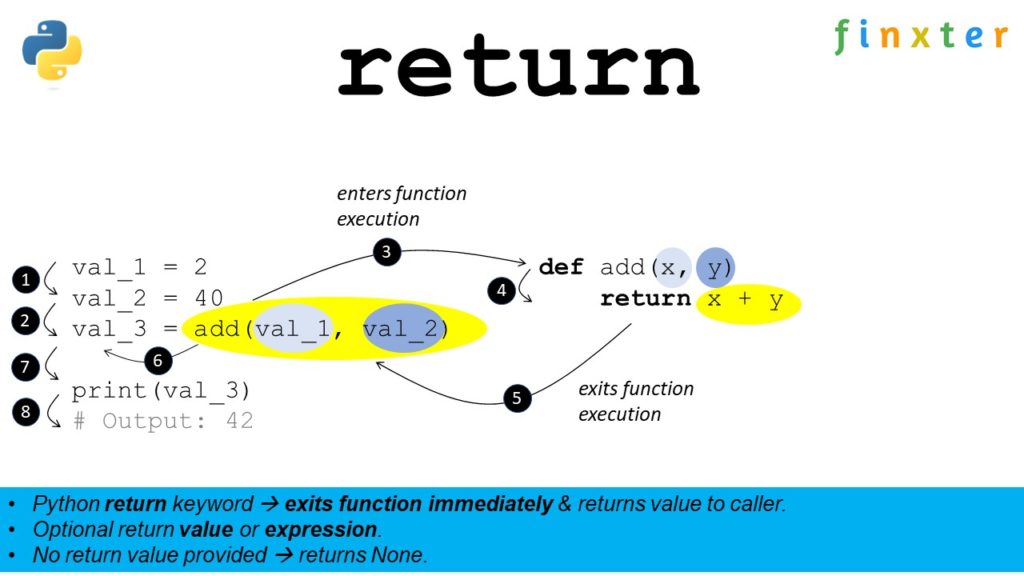
Python 中的函数可以返回多个值，这被称为多返回值。这种机制允许函数将多个数据项作为一个元组返回，极大地增加了代码的灵活性和表达能力。

def divide(a, b):
    quotient = a // b
    remainder = a % b
    return quotient, remainder  # 返回两个值

## 1.2 多返回值的语法结构
在定义函数时，通过逗号分隔多个返回值，Python 会自动将它们封装成一个元组。调用函数时，可以使用多变量接收这些返回值。

q, r = divide(10, 3)  # 接收返回的两个值

## 1.3 多返回值的优势
多返回值使得函数可以传递更多的信息，同时简化了数据的打包和解包过程，减少了代码冗余，提高开发效率。

def employee_info():
    return 'John Doe', 'Engineer', 85000  # 返回姓名、职位和薪水

name, position, salary = employee_info()  # 解包赋值给三个变量

以上章节内容介绍了Python中多返回值的概念和基本用法，为后续章节中深入探讨元组的创建与解包提供了基础。

# 2. 元组的创建与解包原理

## 2.1 元组的基本操作

### 2.1.1 创建元组的方法

元组是Python中一种不可变的序列类型，它可以用来存储一系列的值。元组通常用于存储异构数据，也就是说，一个元组内的元素类型可以各不相同。创建元组的方法多种多样，最简单的是直接用圆括号括起来，并用逗号分隔元素。

# 创建一个空元组
empty_tuple = ()

# 创建一个包含多个元素的元组
single_element_tuple = (1,)
multiple_elements_tuple = (1, 2, 3, 4, 5)

# 使用内置函数tuple创建元组
tuple_from_list = tuple([1, 2, 3])

print(multiple_elements_tuple)
print(tuple_from_list)

在上述代码中，我们使用了两种创建元组的方法：直接使用括号和元素，以及使用`tuple`函数。特别注意，只有一个元素的元组需要用逗号来表示，否则括号会和数学运算优先级混淆，导致创建的是一个普通变量而非元组。

### 2.1.2 元组的基本属性和方法

元组本身是不可变的，这意味着一旦创建完毕，你不能改变其内容。但这并不意味着元组是完全静态的，它还是提供了一些方法来访问和管理数据。

# 假设我们有如下元组
my_tuple = ('apple', 'banana', 'cherry')

# 获取元组的长度
print(len(my_tuple))

# 访问元组中的元素
print(my_tuple[0]) # 输出: apple

# 检查元组中是否存在某个元素
print('banana' in my_tuple)

# 获取元组中最后一个元素的索引
print(my_tuple.index('cherry'))

# 计算某个元素在元组中出现的次数
print(my_tuple.count('banana'))

在上述代码中，我们演示了使用几个基本的属性和方法来操作元组。元组提供的方法包括：`len()`获取元组长度，`in`检查元素是否存在于元组，`index()`获取元素的索引，以及`count()`计算元素出现次数。

## 2.2 解包操作的机制

### 2.2.1 理解解包的本质

解包是Python中的一个强大特性，它允许程序员在赋值时拆分序列（如元组、列表或字符串）和映射（如字典）中的元素。解包的本质在于同时为多个变量赋值。

# 创建一个包含三个元素的元组
my_tuple = (1, 2, 3)

# 通过解包同时为三个变量赋值
a, b, c = my_tuple

print(a) # 输出: 1
print(b) # 输出: 2
print(c) # 输出: 3

在这个例子中，我们首先创建了一个元组`my_tuple`，然后通过解包将三个元素分别赋值给了变量`a`、`b`和`c`。这种方式简化了多个变量赋值的过程，避免了复杂的索引操作。

### 2.2.2 单变量与多变量解包

解包不仅可以应用在变量数量与元组中的元素数量相等的情况下，还可以用于只取元组中的一部分数据。在单变量解包的情况下，可以使用单个星号`*`来收集所有剩余的元素。

# 创建一个包含五个元素的元组
my_tuple = (1, 2, 3, 4, 5)

# 单变量解包，收集所有剩余元素到一个变量
*a, = my_tuple

print(a) # 输出: [1, 2, 3, 4, 5]

在上述代码中，使用`*a`来收集所有剩余元素到列表`a`中，这样的操作非常方便，尤其是在你不知道元组长度的情况下。

在多变量解包的情况下，我们通常指定特定数量的变量来匹配元组中的元素。

# 多变量解包，前三个元素赋值给a, b, c，其余元素赋值给rest
a, b, c, *rest = my_tuple

print(a) # 输出: 1
print(b) # 输出: 2
print(c) # 输出: 3
print(rest) # 输出: [4, 5]

在该例中，`a`、`b`和`c`分别接收了元组中的前三个元素，而剩余的元素则被赋值给列表`rest`。

## 2.3 解包的高级用法

### 2.3.1 星号(*)扩展解包

星号`*`在解包中是一个扩展操作符，它允许我们将元组中的部分元素赋值给一个变量（通常是一个列表），当元组中的元素数量超过变量数量时，这种用法特别有用。

# 创建一个包含七个元素的元组
my_tuple = (1, 2, 3, 4, 5, 6, 7)

# 使用星号(*)扩展解包，前三个元素赋值给a, b, c，剩余元素赋值给rest
a, b, c, *rest = my_tuple

print(a) # 输出: 1
print(b) # 输出: 2
print(c) # 输出: 3
print(rest) # 输出: [4, 5, 6, 7]

在此例子中，`a`、`b`、`c`接收了前三个元素，而`rest`接收了剩余的所有元素。这种用法特别适用于对元组进行部分解包。

### 2.3.2 解包在循环和条件表达式中的应用

解包不仅限于单行赋值语句，它还可以在for循环和条件表达式中使用。

# 在for循环中使用解包
for a, b in [(1, 2), (3, 4), (5, 6)]:
    print(f'({a}, {b})')

# 在条件表达式中使用解包
a, b = (1, 2)
c, d = (3, 4)

if (a, b) == (c, d):
    print("元组相等")
else:
    print("元组不相等")

在这个例子中，解包在for循环中被用来迭代一个元组列表，每次迭代为`a`和`b`赋值。同时，解包在条件表达式中比较两个元组是否相等。

综上所述，元组解包是Python中一个极其有用的特性，它能够简化代码，使数据的处理变得更为直观和高效。通过本章节对元组创建与解包原理的深入分析，你可以更加灵活地运用这些知识，提升你的编程技能。接下来，我们将探索函数多返回值的解包实践，进一步拓展我们对解包操作的理解。

# 3. 函数多返回值的解包实践

函数在Python中是实现逻辑封装的基本单位，而多返