【Alpha Shapes算法的几何魔法】：计算几何基础与数学原理深入解析


# 摘要
Alpha Shapes算法是一种强大的计算几何工具，用于分析和表示点集的形状特征。本文首先概述了Alpha Shapes算法的基本概念和计算几何基础，探讨了几何实体的表示方法、几何图形的基本性质以及算法效率。接着，深入分析了Alpha Shapes的数学原理，包括其定义、性质、参数选择和拓扑结构。在实践应用部分，详细介绍了点集数据的预处理以及Alpha Shapes算法在不同领域的应用实例。最后，本文探讨了算法的优化技术、局限性与挑战，并展望了Alpha Shapes在未来交叉学科中的应用前景以及算法研究的新趋势。

# 关键字
Alpha Shapes算法；计算几何；点集数据；算法优化；多尺度分析；交叉学科应用

参考资源链接：[使用Python和Alpha Shapes算法高效提取点云边缘](https://wenku.csdn.net/doc/5hbwz4x8n1?spm=1055.2635.3001.10343)
# 1. Alpha Shapes算法概述

在数据科学和计算几何的交叉领域中，Alpha Shapes算法是一种强大的工具，用于从无序的点集数据中提取形状和结构信息。本章将对Alpha Shapes算法进行基础性介绍，为读者搭建理解后续章节内容的框架。

## 1.1 算法的定义和应用背景

Alpha Shapes算法，由Edelsbrunner和Mücke提出，是一种用于构建多边形或三维模型的拓扑结构的方法。该算法能够从一组散乱的点集中构建出一个能够反映数据内在结构的连续边界，尤其是在点集中存在噪声或数据不完全时，依然能够提取出有意义的几何特征。

## 1.2 算法的优势和应用场景

与传统的凸包算法相比，Alpha Shapes算法的优势在于其灵活性。它通过一个参数Alpha来控制形状的复杂度，允许从精细到粗糙的各种形状提取。Alpha Shapes在三维空间的点云数据处理、生物信息学以及地理信息系统（GIS）中有着广泛的应用前景。

通过本章的介绍，读者应该能够对Alpha Shapes算法有一个初步的认识，并理解它在数据处理中的重要性。随着文章的深入，将逐步展开对Alpha Shapes更复杂的理论背景和实践应用的探讨。

# 2. 计算几何基础

## 2.1 几何实体的表示方法
在计算几何中，准确地表示点、线、面等基本几何实体是构建复杂算法的基石。几何实体不仅需要以数学模型进行定义，还涉及其在计算机中的表示和运算方式。本节将重点介绍这些基本几何实体的数学模型以及向量运算和几何变换。

### 2.1.1 点、线、面的数学模型
点是几何空间中最基本的元素，通常在二维空间由一对有序数对`(x, y)`表示，而在三维空间则增加一个维度成为`(x, y, z)`。线和面作为由点组成的集合，它们在数学上的表示方法更为丰富。例如，在二维空间中，线可以通过线性方程`Ax + By + C = 0`表示，而在三维空间中，平面也可以通过类似的线性方程`Ax + By + Cz + D = 0`表示。线可以通过两个点定义直线方程，面可以通过三个不共线的点定义平面方程。

### 2.1.2 向量运算和几何变换
向量是计算几何中另一个核心概念，它不仅是几何实体的一种表示方式，还允许我们执行多种几何运算。向量运算包括向量加法、减法、数乘以及点积和叉积等。这些运算在几何变换（例如平移、旋转、缩放）中扮演着关键角色。例如，通过对点表示的向量进行数乘，可以实现缩放操作；通过向量的叉积可以确定三个点构成的平面的法向量，这对于后续章节中的Alpha Shapes算法具有重要意义。

## 2.2 几何图形的基本性质
几何图形的性质描述了它们的基本特征和分类。了解这些性质对于后续算法的设计和优化至关重要。

### 2.2.1 凸包与多边形
凸包是一个重要的概念，它是一个最小的凸多边形，包含给定点集中的所有点。在二维空间中，Graham扫描算法和Jarvis步进算法是常用的凸包计算方法。多边形是具有至少三条边的简单闭合图形。在计算机中，多边形的表示可以通过其顶点序列来进行。

### 2.2.2 点集的划分与分类
点集的划分通常基于某种规则，如将点集划分为凸集和凹集，或基于距离将点集划分为近邻点和远点。这些划分结果对于算法的决策和优化过程至关重要。在几何图形中，点、线、面可以根据其特征被归入不同的类别，比如按照边数将多边形分类为三角形、四边形等，而按照凸性将多边形分类为凸多边形和凹多边形。

## 2.3 几何算法的效率分析
在几何计算中，算法的效率是一个关键因素，通常通过时间复杂度和空间复杂度来衡量。

### 2.3.1 时间复杂度与空间复杂度
时间复杂度是衡量算法执行时间与输入数据规模之间关系的度量，常用大O符号表示。空间复杂度则是衡量算法在运行过程中占用存储空间的大小。例如，对于点集数据进行凸包计算，Jarvis步进算法的时间复杂度为O(nh)，其中n是点的数量，h是凸包点的数量。

### 2.3.2 优化算法的关键策略
优化算法通常涉及减少不必要的计算、避免重复计算、使用更高效的算法和数据结构等策略。例如，在凸包计算中，如果可以预先知道一部分凸包点，则可以减少后续计算量。此外，选择合适的算法对于性能提升至关重要，如将递归算法改写为迭代算法有时可以提高性能。

graph TD
    A[开始] --> B[数据预处理]
    B --> C[选择基础算法]
    C --> D[算法优化]
    D --> E[结果输出]
    E --> F[结束]

上述流程图展示了从数据预处理到结果输出的一般算法处理流程，其中每个步骤都可能包含对时间复杂度和空间复杂度的考虑。在几何算法中，每个步骤都必须精心设计，以确保整体性能的最优化。

在计算几何领域，对于点、线、面的数学模型及其表示，以及向量运算和几何变换的理解是基础。几何图形的基本性质和分类方法为后续的算法实现打下扎实的基础。而对几何算法效率的分析，包括时间和空间复杂度的考量，以及优化算法的关键策略，则是实现高性能计算几何应用的关键。以上这些内容构成了后续深入探讨Alpha Shapes算法的基础，为其提供了坚实的理论和实践基础。

# 3. Alpha Shapes的数学原理

Alpha Shapes算法是一种用于描述和识别多维数据点集中形状的几何构造技术。它的核心是Alpha参数，该参数控制着形状的粗糙度与细节。理解这一算法的数学原理对于应用Alpha Shapes解决实际问题至关重要。本章将深入探讨Alpha Shapes的定义、性质、以及Alpha参数的作用。此外，本章还将分析Alpha Shapes的拓扑结构，以及其边、顶点和面的生成规则。

## 3.1 Alpha Shapes的定义与性质

Alpha Shapes不仅在计算几何学领域中占有一席之地，而且在多个学科中都有广泛的应用，如计算机图形学、分子生物学和地理信息系统等。其定义和性质的深入理解，有助于我们更好地利用这一工具。

### 3.1.1 Alpha Shapes的几何含义

Alpha Shapes是一种基于点集的几何结构，可以通过设置不同的Alpha值来调整其形态。在一个二维空间中，Alpha Shapes可以理解为在一个点集内形成一个能够包含所有点的最小凸包。当Alpha值设置为无穷大时，Alpha Shapes退化为这个凸包；当Alpha值减少到某个点集特定的特征值时，Alpha Shapes则会转变为最接近该点集拓扑特性的结构，甚至能识别出空洞和边界。

### 3.1.2 形态学滤波与形态学开闭运算

形态学滤波是一种使用预定义结构元素对图像进行处理的数学方法，而Alpha Shapes与形态学滤波有着紧密的联系。通过调整Alpha值，可以执行形态学开闭运算。形态学开运算能够去除小的凸出部分，而形态学闭运算则可以填补小的空洞。Alpha Shapes在处理点云数据时，可以模拟这些操作，使数据更加平滑和规律。

## 3.2 Alpha参数的作用与选择

Alpha参数在Alpha Shapes算法中起着决定性的作用，它直接决定了所得到的形状的粗糙程度。

### 3.2.1 参数对形状复杂度的影响

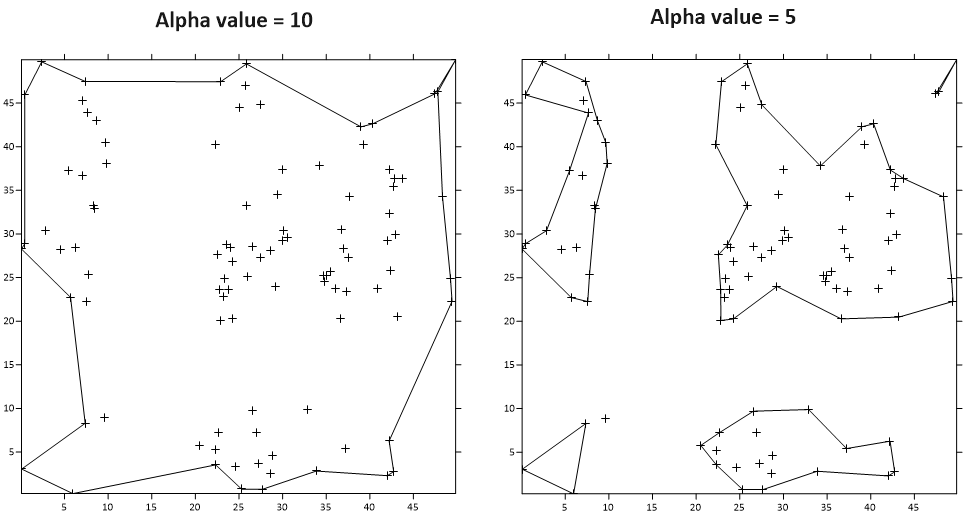
Alpha值的大小直接影响了Alpha Shapes的复杂度。当Alpha值较大时，所得到的形状较为平滑，能够忽略数据点中的小凹凸和噪声，但同时可能会丢失一些有意义的特征。反之，较小的Alpha值会捕捉到更