【概率论基础】：掌握随机过程概率空间与随机变量，不再迷茫


# 摘要
本文旨在介绍概率论的核心概念、构建概率空间的性质、随机变量的分类及其概率分布、多维随机变量的相关性以及随机过程的基本理论与分类。通过深入分析概率空间的定义、公理化定义、以及概率的计算方法，本文为读者提供了概率论的坚实基础。在随机变量及其分布章节，文章详细探讨了不同类型的随机变量、分布函数与密度函数，以及常见概率分布的应用。随后，本文进一步阐述了多维随机变量的联合分布、独立性、相关系数和函数的分布。最后，文章介绍了随机过程的描述、分类、主要类型和统计特性，并通过多个实际应用案例，展示了随机过程在自然科学、工程技术以及计算机科学中的广泛应用。

# 关键字
概率论；概率空间；随机变量；概率分布；多维随机变量；随机过程

参考资源链接：[随机过程复习题（含答案）](https://wenku.csdn.net/doc/6412b4b9be7fbd1778d40971?spm=1055.2635.3001.10343)
# 1. 概率论的起源与基本概念

## 1.1 概率论的历史脉络

概率论起源于17世纪，当时的法国赌徒和意大利数学家开始对赌博中出现的问题进行数学上的探讨。他们试图找出决定游戏胜负的关键因素，并预测结果发生的可能性。这一数学分支最初主要用于解决赌博中遇到的问题，随后逐步发展成为一门严谨的数学学科。

## 1.2 基本概念的界定

概率论的基本概念包括事件、概率和随机变量。**事件**是随机实验中结果的集合，而**概率**是衡量一个事件发生可能性大小的数学度量。**随机变量**则是将样本空间中的每一个元素映射到实数线上的一个变量。这三个概念是概率论分析任何随机现象的基石。

## 1.3 理论的重要性与应用

概率论不仅在数学理论研究中占据重要地位，它在实际生活中的应用也极为广泛。例如，天气预报、保险精算、金融市场分析以及公共卫生政策等领域都广泛应用了概率论的原理和方法。随着科技的进步，概率论在数据分析、机器学习和人工智能领域的重要性日益凸显。

# 2. 概率空间的构建与性质

## 2.1 概率空间的定义与组成

### 2.1.1 样本空间

概率空间是概率论的基本概念之一，它由样本空间、事件及其运算组成。样本空间是指进行随机试验的所有可能结果组成的集合，通常用大写字母S表示。每一个样本点是样本空间中的一个元素，代表了一个可能发生的简单事件。

在构建样本空间时，需要明确随机试验的定义和可能的结果。例如，抛掷一枚硬币的样本空间可以表示为S = {正面, 反面}。对于掷骰子，样本空间则包含了六个元素，S = {1, 2, 3, 4, 5, 6}。

### 2.1.2 事件及其运算

事件是从样本空间中选取的一个或多个结果组成的集合。单个样本点是一个基本事件，而包含两个或更多样本点的组合则称为复合事件。事件可以进行各种集合运算，如并集、交集和补集。

- 并集运算：A ∪ B 表示事件A和事件B至少有一个发生的事件。
- 交集运算：A ∩ B 表示事件A和事件B同时发生的事件。
- 补集运算：A' 表示事件A不发生的事件。

例如，在掷骰子的试验中，事件A为得到偶数点，事件B为得到3以上的点数，则 A = {2, 4, 6}，B = {3, 4, 5, 6}。事件A和B的并集A ∪ B表示得到偶数或3以上的点数，A ∩ B表示同时得到偶数和3以上的点数，即得到4或6点。

## 2.2 概率的公理化定义

### 2.2.1 古典概型

古典概型是概率论中一种简单而重要的模型。它假设随机试验的每个简单事件发生的概率相等，且所有事件是等可能的。在古典概型中，事件A的概率定义为：

P(A) = 有利事件数 / 样本空间的总数

例如，在掷硬币的试验中，样本空间S = {正面, 反面}，如果要求得到正面的概率，那么 P(正面) = 有利事件数 / 样本空间的总数 = 1/2。

### 2.2.2 几何概型

几何概型是基于几何空间的模型，其中的概率与几何区域的长度、面积或体积成比例。在这种情况下，事件的概率与其所占据的几何位置相关。

例如，在投掷飞镖的游戏中，飞镖落在靶心的概率与靶心面积大小有关。如果靶心的面积是整个靶面的1/4，那么飞镖落在靶心的概率就是1/4。

### 2.2.3 条件概率与贝叶斯定理

条件概率是指在已知某些信息或条件发生的前提下，求另一事件发生的概率。条件概率的定义是：

P(A|B) = P(A ∩ B) / P(B)

当P(B)不为0时，事件A在事件B发生的条件下发生的概率是事件A与B同时发生的概率除以事件B发生的概率。

贝叶斯定理是概率论中的一个重要公式，它提供了从条件概率反推出无条件概率的方法。贝叶斯定理的公式是：

P(B|A) = P(A|B) * P(B) / P(A)

利用贝叶斯定理，可以解决诸如诊断测试中，根据测试结果来推断患病概率的问题。

## 2.3 概率的计算方法与实践应用

### 2.3.1 组合数学在概率论中的应用

组合数学是研究离散对象组合方式的数学分支，在概率论中尤为关键。许多问题可以通过组合数学的方法来求解概率问题。例如，计算掷骰子得到特定点数的组合方式数，可以使用组合数公式C(n, k)表示。

以下是计算掷骰子得到5或6点的组合数的一个例子：

# 计算得到5或6点的组合数
import math

# 样本空间大小
n = 6

# 有利事件数：掷出5或6点
k = 2

# 计算组合数C(n, k)
有利事件数 = math.comb(n, k)

# 计算总概率
总概率 = 有利事件数 / (n ** k)

print("有利事件数:", 有利事件数)
print("掷出5或6点的概率:", 总概率)

这段代码计算了掷一个骰子两次，至少得到一个5或6点的概率。通过组合数学的原理，我们可以使用`math.comb`函数来计算得到5或6点的组合方式数。

### 2.3.2 实际问题的概率计算实例

实际问题中，概率计算往往涉及到更复杂的模型和数据。例如，在市场调研中，可能需要计算某一产品被接受的概率，这涉及到对目标群体的深入了解和市场条件的综合分析。

下面，我们用一个简化的例子来说明：

假设在一个市场调研中，有50%的受访者表示他们更倾向于购买新型号产品。现在需要对10位随机选出的受访者进行调查，计算其中至少有8位表示愿意购买的概率。

这是一个典型的二项分布问题，可以用二项分布公式来解决。二项分布的概率质量函数为：

P(X = k) = C(n, k) * p^k * (1-p)^(n-k)

其中，`n`是试验次数（受访者人数），`k`是成功次数（表示愿意购买的人数），`p`是单次试验的成功概率（愿意购买的概率）。

import math
from scipy.stats import binom

# 参数设定
n = 10           # 受访者人数
p = 0.5          # 愿意购买的概率
k_values = range(8, 11)  # 想要计算的概率区间

# 计算概率
for k in k_values:
    probability = binom.pmf(k, n, p)
    print(f"恰好有{k}位受访者表示愿意购买的概率为: {probability}")

在这个例子中，我们使用了`scipy.stats`模块中的`binom`类来计算恰好有8位、9位和10位受访者表示愿意购买的概率。

结合实际问题，概率论不仅能够帮助我们更好地理解和预测未来，还能指导我们做出更加合理的决策。无论是自然科学、工程技术还是社会科学，概率论都发挥着不可或缺的作用。

# 3. 随机变量及其分布

在概率论和统计学中，随机变量及其分布是理解随机现象内在规律的关键。随机变量是从概率空间到实数线的映射，其取值带有随机性。而概率分布则是随机变量取各个值的可能性大小的描述。本章将深入探讨随机变量的概念、分类以及常见的概率分布，并通过实例展示其在实际中的应用。

## 3.1 随机变量的概念与分类

随机变量是理解随机现象的桥梁。在讨论随机变量之前，先要清楚随机变量并不是一个固定的数值，而是一个可以取不同值的量，每个值都对应一个概率。

### 3.1.1 离散随机变量与连续随机变量

根据随机变量取值的性质，可以分为离散随机变量和连续随机变量：

- **离散随机变量**：只取有限个或可数无限个值的随机变量。例如，抛硬币的结果（正面或反面），或者投掷骰子的点数（1到6）。离散随机变量的概率分布可以用概率质量函数（PMF）来描述，表示变量取每一个具体值的概率。

    (* 例如，二项分布的PMF *)
    PMF[x_, n_, p_] := Binomial[n, x] * p^x * (1 - p)^(n - x)

在上述代码块中，`PMF` 函数计算了离散随机变量x服从二项分布（参数为n次试验，每次试验成功的概率为p）的概率质量函数。

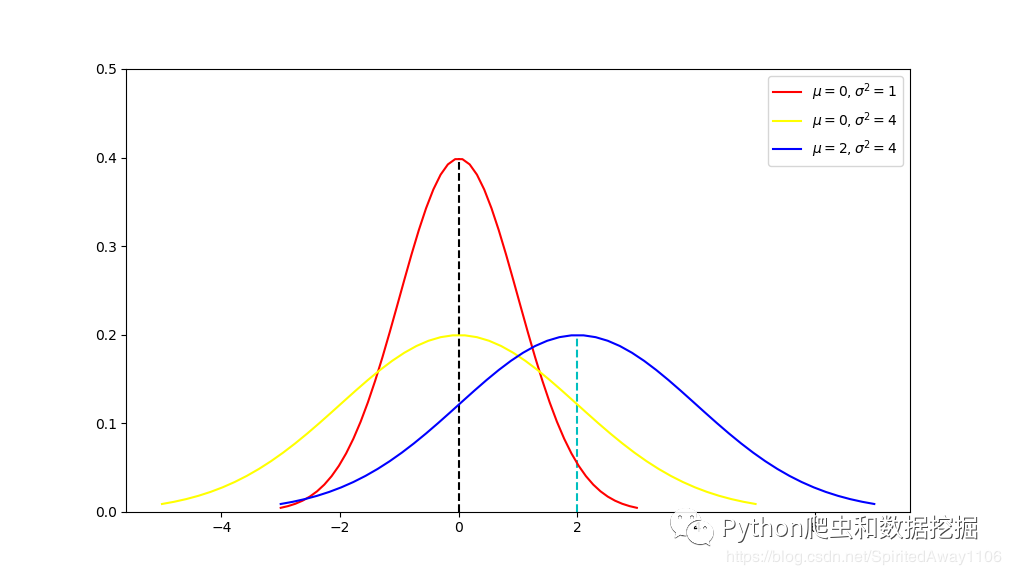
- **连续随机变量**：可以取某个区间内任意值的随机变量。连续随机变量的概率分布可以通过概率密度函数（PDF）来描述。概率密度函数在任何区间内的积分等于该区间内随机变量取值的概率。

    import scipy.stats as stats
    import matplotlib.pyplot as plt

    # 生成正态分布数据
    x = np.linspace(-3, 3, 100)
    y = stats.norm.pdf(x, 0, 1)

    # 绘制概率密度函数
    plt.plot(x, y)
    plt.title('Normal Distribution PDF')
    plt.xlabel('x')
    plt.ylabel('Density')
    plt.show()

在这段Python代码中，我们使用了`scipy.stats`模块来绘制标准正态分布的概率密度函数。`x`是值的范围，`y`是对应的密度值。绘图部分使用了`matplotlib`库。

### 3.1.2 随机变量的函数

随机变量的函数同样是一个随机