【LS-PrePost网格编辑进阶】：高级技巧助你掌握网格艺术


参考资源链接：[LS-PrePost：高级前处理与后处理全面教程](https://wenku.csdn.net/doc/22ae10d9h1?spm=1055.2635.3001.10343)
# 1. LS-PrePost网格编辑概览

在计算机辅助工程领域，网格编辑是一项关键的技术，它允许工程师和研究人员在复杂的模拟环境中对几何模型进行精确的控制。LS-PrePost作为一款功能强大的前后处理软件，提供了一个综合的环境来创建、编辑和优化有限元网格。

## 1.1 网格编辑的重要性

网格编辑是数值分析中的基石，特别是在有限元分析（FEA）和计算流体动力学（CFD）等领域。精确的网格能够为模拟提供准确的结果，减少错误和不确定性，从而提高模拟的可靠性。网格编辑涉及创建或修改网格以满足特定的分析要求，例如提升计算精度或降低计算成本。

## 1.2 LS-PrePost在网格编辑中的作用

LS-PrePost提供了一系列工具和功能，使得工程师能够有效地管理整个网格编辑流程。从基本的网格创建到高级的优化和编辑，LS-PrePost通过直观的用户界面和丰富的内置功能，简化了网格设计的复杂性。此外，它还支持自动化脚本和宏，这可以进一步提升网格编辑的效率。

## 1.3 本章学习目标

本章的目标是为读者提供LS-PrePost网格编辑的初步认识，包括软件界面的介绍、基础操作流程，以及网格编辑在工程模拟中的应用。我们将通过案例演示如何使用LS-PrePost进行网格的创建和编辑，从而为接下来深入探讨网格创建与编辑的理论基础打下坚实的基础。

# 2. 网格创建与编辑的理论基础

网格技术是计算流体力学（CFD）、有限元分析（FEA）以及其他工程模拟领域不可或缺的一部分。一个良好的网格结构可以大大提高模拟的精确度和效率。本章将深入探讨网格创建与编辑过程中的理论基础，为读者提供坚实的理论支撑。

## 2.1 网格结构的基本概念

### 2.1.1 网格类型与特性

网格是将连续的物理空间离散化为有限数量的单元，以便于数值求解过程。根据其结构，网格可以分为结构网格和非结构网格。

- **结构网格**（Structured Grids）：这类网格通常由规则排列的单元组成，如正方形或六面体，易于生成，并能高效地表示流体流动的规则区域。结构网格的缺点在于难以适应复杂的几何形状。
- **非结构网格**（Unstructured Grids）：与结构网格不同，非结构网格由不规则的单元组成，如三角形、四面体等。这种类型的网格能够较好地适应复杂的几何边界，但其计算成本通常更高。

### 2.1.2 网格质量评估标准

网格质量对计算模拟结果的准确性至关重要。一个高质量的网格应满足以下标准：

- **正交性**（Orthogonality）：单元的各个面应尽可能垂直相交。
- **等角性**（Isotropy）：单元的形状应尽可能接近正多边形或多面体。
- **尺寸变化**（Size Variation）：网格在不同区域的尺寸应平滑变化，避免尺寸突变。
- **网格密度**（Mesh Density）：需要重点分析的区域应具有较高的网格密度。

## 2.2 网格生成的数学原理

### 2.2.1 网格生成算法

网格生成算法是将几何模型转换为计算网格的过程。常见的算法包括：

- **四叉树/八叉树**（Quadtree/Octree）：递归地将空间划分为更小的单元。
- **Delaunay三角化**：为一组点生成一组互不重叠且最大化最小角的三角形。
- **推进前沿法**（Advancing Front Method）：基于几何边界逐层推进生成网格。

### 2.2.2 网格加密与稀疏化方法

- **网格加密**（Mesh Refinement）：为了提高某些区域的模拟精度，可以对这些区域进行网格细化。
- **网格稀疏化**（Mesh Coarsening）：通过合并小单元为大单元来减少计算量。

## 2.3 网格编辑中的材料模型理论

### 2.3.1 材料属性的网格表示

网格不仅用于模拟几何形状，还需承载物理和材料属性。例如，在有限元分析中，每个单元可能具有不同的弹性模量、密度、热导率等属性。

### 2.3.2 边界条件在网格中的应用

边界条件在网格中的应用决定了物理问题的约束条件，常见的边界条件类型包括：

- **狄利克雷边界条件**（Dirichlet Conditions）：指定解在边界上的值。
- **诺伊曼边界条件**（Neumann Conditions）：指定解在边界上的法向导数。

以上是网格创建与编辑理论基础的简要介绍。这些基础理论对理解后续章节中的技巧和应用至关重要。下一部分，我们将深入探讨网格生成的数学原理及其在实际操作中的应用。

# 3. LS-PrePost网格编辑技巧

## 3.1 网格生成的高级操作

### 3.1.1 控制点与网格划分技术

在高级网格编辑中，控制点技术用于精确地指导网格生成过程，以适应复杂的几何形状和变化的物理量分布。通过在几何模型的关键位置定义控制点，网格划分算法能够生成与控制点相关联的网格，从而使得网格在这些关键区域具有更高的分辨率。

例如，在LS-PrePost中，用户可以定义控制点，然后选择适当的网格划分策略，如映射网格或四边形/六面体网格。使用控制点技术时，网格生成器会尝试在控制点处创建高质量的网格单元，同时保持整个区域网格的一致性和光滑性。

graph LR
A[开始] --> B[定义几何模型]
B --> C[设置控制点]
C --> D[选择网格划分策略]
D --> E[生成网格]

控制点的设置通常需要一定的领域经验，以确保网格的质量和计算效率。控制点设置不当可能会导致网格质量下降或计算资源浪费。

### 3.1.2 自适应网格生成技术

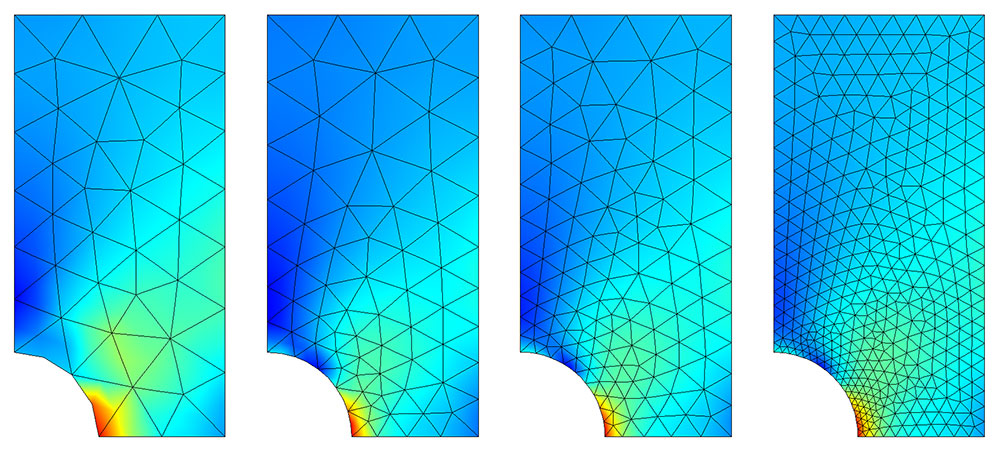
自适应网格生成技术是一种动态调整网格密度的方法，通常用于提高计算精度和减少计算成本。自适应网格技术根据物理场的分布或梯度信息自动调整网格的大小和形状，确保在关键区域有较高的网格分辨率。

在LS-PrePost中，用户可以根据模拟结果的误差估计来指导网格的自适应调整。例如，在热传导分析中，温度梯度较大的区域需要更细致的网格以捕获精确的温度变化。通过执行一系列迭代计算，并根据误差指标对网格进行自适应细化或粗化，可以达到提高计算精度的目的。

graph LR
A[开始] --> B[进行初步网格划分]
B --> C[执行初始模拟]
C --> D[计算误差指标]
D --> E[根据误差指标自适应调整网格]
E --> F[重复模拟直到满足精度要求]

自适应网格技术需要较高的计算资源，并且在网格生成和模拟过程中需要反复迭代，但在处理复杂问题时，这种方法可以显著提高计算效率和精度。

## 3.2 网格编辑与优化

### 3.2.1 网格简化与优化策略

网格简化是指通过算法减少网格单元的数量，以降低计算复杂性和节省资源，同时尽可能保持模型的精确度。优化策略通常涉及移除不必要的网