SciPy和NumPy深度学习：Anaconda中的高效科学计算基础

# 1. SciPy和NumPy简介

在现代科学计算和数据分析领域，**SciPy** 和 **NumPy** 库是Python编程语言中不可或缺的工具。本章将为读者提供这两个库的基础知识概览，并探讨它们在数据科学中的重要性。

## 1.1 Python中的科学计算

Python语言因其简洁和可读性在科学计算社区中获得了广泛的认可。SciPy和NumPy正是基于Python的开源软件包，它们提供了一系列高效的数值计算和科学计算功能，使得Python成为数据科学和工程领域的强大工具。

## 1.2 SciPy库的特点

SciPy是一个专门用于数学、科学和工程计算的开源库，它建立在NumPy基础之上，提供了各种算法的实现，包括优化、线性代数、积分和统计等。它旨在快速处理科学任务，支持高级数据处理和分析。

## 1.3 NumPy库的作用

NumPy是SciPy库的基础，专注于提供一个强大的N维数组对象ndarray。它提供对大型多维数组和矩阵运算的快速、灵活的操作。NumPy中的数组是同质的，这意味着它们包含相同类型的数据，并且操作通常比原生Python更快。

通过本章的学习，您将对NumPy和SciPy有初步的理解，并能够把握其在后续章节中如何应用于更复杂的科学计算和数据分析任务。接下来，我们将深入探讨NumPy的核心概念，开始构建高效计算的基础。

# 2. NumPy基础与数据结构

在深入探讨NumPy的高级功能和应用之前，我们需要对其基础数据结构有一个全面的了解。NumPy数组是数值计算的核心，它的性能和灵活性使其成为处理大数据集和进行科学计算的首选工具。本章节将深入探究NumPy数组的核心概念、计算功能以及高级特性。

## 2.1 NumPy数组的核心概念

### 2.1.1 数组创建与维度操作

NumPy数组的创建是进行科学计算的第一步。我们可以使用多种方式来创建一个数组，包括从Python列表直接转换或者使用NumPy的内置函数。一旦数组被创建，我们通常需要对其进行维度操作以适应特定的数据处理需求。以下是如何创建和操作数组的一些基础示例：

import numpy as np

# 从列表创建数组
a = np.array([1, 2, 3])

# 创建一个多维数组
b = np.array([[1, 2, 3], [4, 5, 6]])

# 使用np.zeros创建指定大小的全零数组
c = np.zeros((2, 3))

# 使用np.ones创建指定大小的全一数组
d = np.ones((3, 2))

# 使用np.arange创建一个有序数组
e = np.arange(10)

# 使用np.linspace创建包含指定数量元素的数组
f = np.linspace(0, 1, 5)

在创建多维数组时，理解数组的维度（shape）和步长（stride）非常重要。数组的维度告诉我们每个维度的大小，而步长则是在内存中检索数组元素时每一维增加的字节数。

维度操作主要包括改变数组的形状（reshape）、增加新的维度（newaxis）、合并数组（concatenate）和数组的转置（transpose）等。例如，以下是一些常见的维度操作代码：

# 改变数组形状
f = e.reshape(2, 5)

# 在第二维度前增加一个新的维度
g = f[np.newaxis, :]

# 合并两个数组
h = np.concatenate((a, b))

# 数组转置
i = g.T

### 2.1.2 索引和切片技术

索引和切片是数组操作中不可或缺的部分，它们允许我们从数组中提取特定的元素或者子数组。NumPy的索引机制非常灵活，支持整数索引、切片索引、布尔索引和花式索引。

# 使用整数索引获取单个元素
j = a[1]

# 使用切片索引获取子数组
k = b[0, 1:]

# 使用布尔索引
l = b[b > 2]

# 使用花式索引，创建一个索引列表
m = b[[0, 1, 0], [1, 2, 1]]

在上述代码中，`l = b[b > 2]` 这行代码利用了一个布尔数组来从 `b` 中选择所有大于 2 的元素。花式索引则通过一个索引数组来选择元素，这在处理多维数据时非常有用。

索引和切片技术的灵活性使得我们可以进行复杂的数据操作，这是进行高效数据分析的关键。

## 2.2 NumPy数组的计算功能

### 2.2.1 广播机制和通用函数

NumPy的广播机制允许不同形状的数组进行数学运算。这在实际应用中极为有用，尤其是当我们需要在数组的一个维度上重复操作时。下面是一个简单的广播示例：

# 一个一维数组和二维数组的广播操作
a = np.array([1, 2, 3])
b = np.array([[1, 2, 3], [4, 5, 6]])

# 广播机制允许a与b进行元素级别的加法
c = a + b

在上述示例中，一维数组 `a` 被自动扩展为二维数组，以便与 `b` 的每一行相加。如果两个数组的维度不匹配，但它们在某些维度上的大小是相同的或者一个是1，NumPy将自动进行广播。

通用函数（ufunc）提供了一系列对数组中每个元素执行快速、元素级计算的函数。这些函数在NumPy中被高度优化，执行速度快，是进行数值计算的核心工具。

### 2.2.2 线性代数、统计和随机数生成

NumPy提供了丰富的线性代数计算功能，包括矩阵乘法、矩阵求逆、特征值分解等。线性代数的函数大都包含在 `numpy.linalg` 模块中。以下是一个简单的线性代数示例：

import numpy.linalg as la

# 创建一个3x3的矩阵
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# 计算矩阵的逆
A_inv = la.inv(A)

在统计方面，NumPy提供了计算均值、中位数、标准差等常用的统计函数。它们位于 `numpy` 模块中，可以对整个数组或者数组的特定轴进行操作。例如：

# 计算数组的均值
mean_value = np.mean(a)

# 计算数组的标准差
std_dev = np.std(a)

随机数生成是数据分析和模拟的另一个重要部分。NumPy提供了多种方法来生成随机数，这些方法都封装在 `numpy.random` 模块中。例如：

# 生成一个均匀分布的随机数
random_number = np.random.rand()

# 生成一个正态分布的随机数
normal_number = np.random.randn()

## 2.3 NumPy数组的高级特性

### 2.3.1 结构化数组和记录数组

结构化数组和记录数组是NumPy数组的两种特殊类型，允许数组的元素是复合数据类型，比如由不同数据类型的字段组成的结构体。这在处理结构化数据，如表格数据或者与数据库相关的数据时非常有用。

# 创建一个结构化数组
dt = np.dtype([('name', 'S10'), ('age', 'i4')])
people = np.array([("Alice", 30), ("Bob", 25)], dtype=dt)

# 访问结构化数组中的字段
names = people['name']
ages = people['age']

在上述示例中，我们首先定义了一个数据类型 `dt`，它包含两个字段：`name` 和 `age`。然后，我们创建了一个结构化数组 `people`，并存储了一些人的姓名和年龄。最后，我们访问了 `name` 和 `age` 字段。

### 2.3.2 性能考量与内存使用

NumPy数组相比于Python原生的列表和元组，提供了更高的性能和更低的内存消耗。这是因为NumPy数组在内存中连续存储数据，并且所有元素都具有相同的数据类型，这使得CPU缓存的使用更加高效。通过使用NumPy数组，可以显著提高计算密集型任务的性能。

为了更有效地使用内存，NumPy提供了一系列的内存管理工具，如 `np.DataSource` 来载入数据，`np.zeros` 和 `np.ones` 来创建初始化数组，以及 `np.copy` 来复制数组。此外，通过使用视图和拷贝的概念，我们可以更精确地控制数据在内存中的使用和复制。

在处理大规模数据集时，了解和掌握NumPy的内存使用和性能优化知识是非常重要的。它可以帮助开发者编写出既快速又高效的数值计算代码。

# 3. SciPy库的科学计算能力

SciPy库是Python中用于科学和技术计算的标准库之一，它建立在NumPy之上，提供了许多用于解决科学计算问题的高级工具。SciPy构建了多样的子模块，使得用户能够方便地解决各类数学、科学、工程问题。在本章节中，我们将深入探索SciPy库的核心功能和应用，以理解其如何提升数据处理和科学计算的效率。

### 3.1 SciPy的子模块概述

SciPy提供了一系列子模块，每个子模块针对特定领域的问题提供了功能丰富的函数集合。我们将重点探讨优化器、积分和常微分方程求解器以及线性代数扩展和稀疏矩阵操作。

#### 3.1.1 优化器、积分和常微分方程求解器

SciPy的`optimize`模块提供了一系列用于解决优化问题的工具。这些问题包括无约束和有约束的最优化问题，以及全局优化。在实际应用中，诸如工程设计、经济模型分析等领域都需要运用这些优化算法。

例如，使用`scipy.optimize.minimize`函数求解一个简单的目标函数的最小值：

from scipy.optimize import minimize

def objective_function(x):
    return x[0]**2 + x[1]**2

x0 = [1.35, 0.881]  # 初始猜测值
result = minimize(objective_function, x0)

print(result)

在上述代码中，我们定义了一个目标函数`objective_function`，该函数接受一个变量`x`，并返回`x[0]**2 + x[1]**2`的结果，我们的目标是找到使该函数值最小的`x`值。通过调用`minimize`函数并提供初始猜测值`x0`，我们可以找到函数的局部最小值。

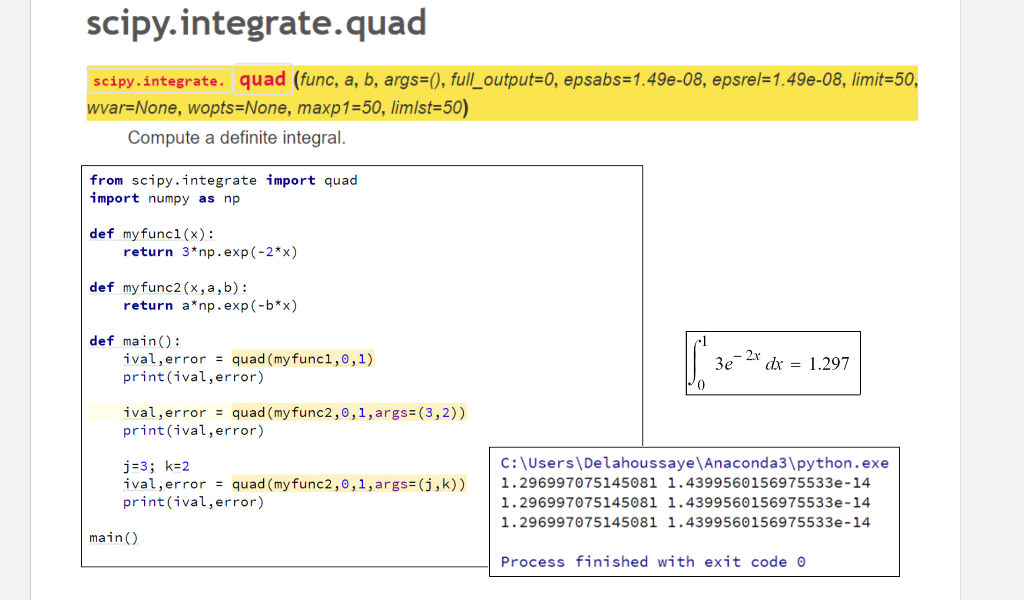
SciPy中的积分子模块提供了