功率因数校正的仿真与建模：预测性能，优化设计

# 1. 功率因数校正的基本原理**

功率因数是衡量交流电路中有效功率与视在功率之比的指标，反映了电能利用效率。功率因数低会导致电网损耗增加、电能浪费，并对电网稳定性产生负面影响。

功率因数校正（PFC）是一种技术，通过增加电路中的无功功率分量，提高功率因数。无功功率不产生实际功，但会占用电网容量，导致电网损耗。PFC通过添加电容器或电感等无功元件，抵消电路中的感性或容性无功功率，从而提高功率因数。

# 2. 功率因数校正仿真建模

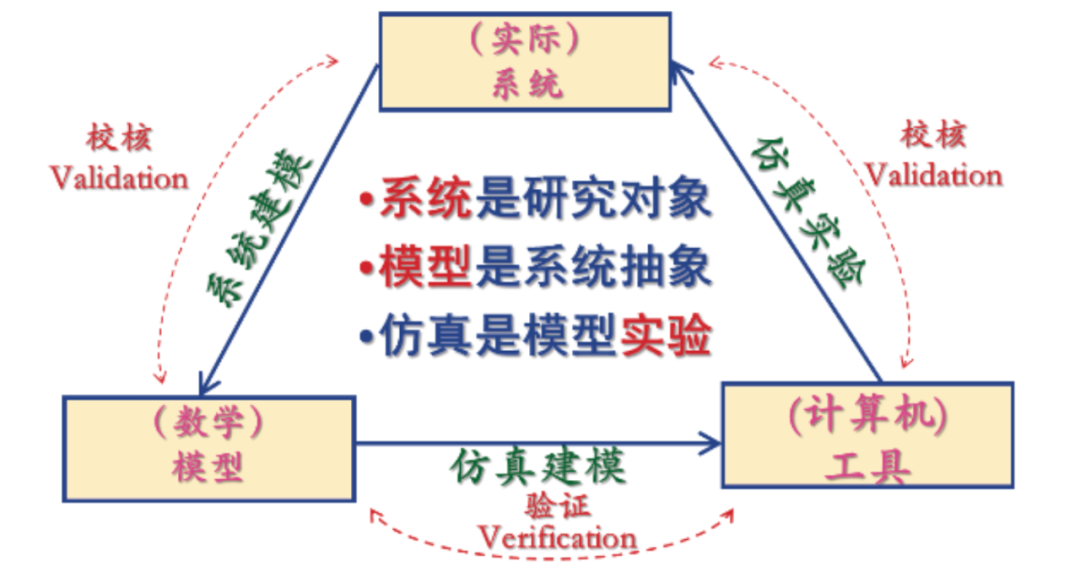
功率因数校正仿真建模是通过建立数学模型来模拟功率因数校正器的行为，为其设计、优化和性能评估提供依据。

### 2.1 数值建模方法

#### 2.1.1 等效电路模型

等效电路模型将功率因数校正器简化为一个由电阻、电感和电容等元件组成的电路网络。这种模型易于建立和分析，适用于稳态和瞬态条件下的基本特性研究。

// 等效电路模型代码块
import numpy as np
import matplotlib.pyplot as plt

# 电路参数
R = 10  # 电阻（欧姆）
L = 0.1  # 电感（亨利）
C = 100e-6  # 电容（法拉）

# 输入电压
V_in = 100  # 输入电压（伏特）
f = 50  # 输入频率（赫兹）

# 计算阻抗
Z = R + 1j * 2 * np.pi * f * L - 1j / (2 * np.pi * f * C)

# 计算功率因数
pf = np.cos(np.angle(Z))

# 打印结果
print("阻抗：", Z)
print("功率因数：", pf)

# 绘制波形
t = np.linspace(0, 0.1, 1000)
v_in = V_in * np.sin(2 * np.pi * f * t)
i_in = v_in / Z
plt.plot(t, v_in, label="输入电压")
plt.plot(t, i_in, label="输入电流")
plt.legend()
plt.show()

**逻辑分析：**

* `Z`计算电路的阻抗，包括电阻、电感和电容的影响。
* `pf`计算功率因数，即阻抗的相位角余弦值。
* 绘制输入电压和电流波形，展示功率因数校正器的动态响应。

#### 2.1.2 状态空间模型

状态空间模型将功率因数校正器描述为一组微分方程，其中状态变量代表电路的能量存储元件（电感和电容）的状态。这种模型适用于复杂系统的动态分析和控制设计。

// 状态空间模型代码块
import numpy as np
import scipy.integrate as integrate

# 电路参数
L = 0.1  # 电感（亨利）
C = 100e-6  # 电容（法拉）
R = 10  # 电阻（欧姆）

# 输入电压
V_in = 100  # 输入电压（伏特）

# 状态变量
x = np.array([0, 0])  # 电感电流和电容电压

# 微分方程
def dxdt(t, x):
    i_L = x[0]
    v_C = x[1]
    di_Ldt = (V_in - v_C - i_L * R) / L
    dv_Cdt = (i_L - v_C / R) / C
    return np.array([di_Ldt, dv_Cdt])

# 求解微分方程
t_span = [0, 0.1]  # 时间范围
sol = integrate.solve_ivp(dxdt, t_span, x, method="RK45")

# 打印结果
print("电感电流：", sol.y[0, -1])
print("电容电压：", sol.y[1, -1])

# 绘制波形
p