揭秘自平衡树的奥秘：从原理到应用的全面解析

# 1. 自平衡树的基本原理**

自平衡树是一种数据结构，它可以自动保持其平衡，即使在插入或删除元素后也是如此。这使得自平衡树在需要快速插入、删除和搜索操作的应用中非常有用。

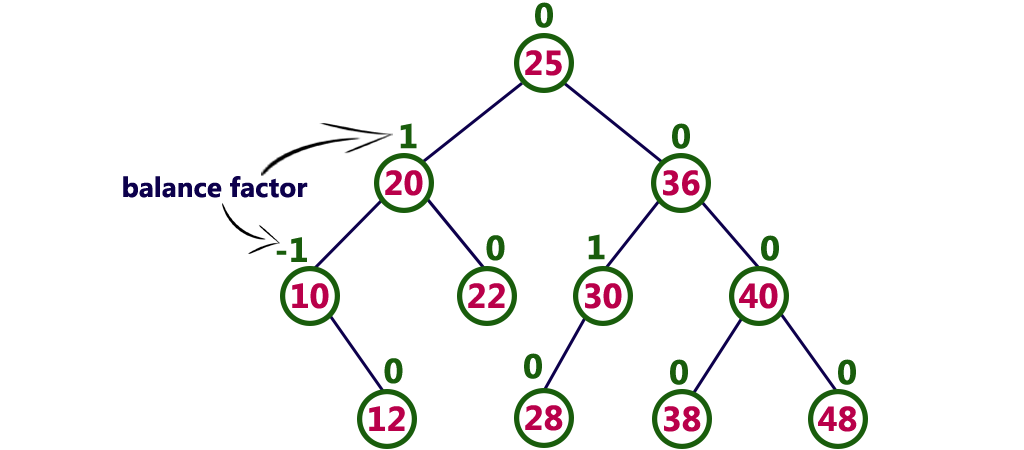
自平衡树的关键思想是维护一个平衡因子，该因子表示子树的高度差。当平衡因子超出允许范围时，树将进行旋转操作以恢复平衡。通过保持平衡，自平衡树可以确保其操作的效率，无论树的大小如何。

# 2. 自平衡树的实现

### 2.1 红黑树

#### 2.1.1 红黑树的定义和性质

红黑树是一种自平衡二叉查找树，它满足以下性质：

- **每个节点要么是红色，要么是黑色。**
- **根节点始终是黑色。**
- **每个叶节点（NIL）都是黑色。**
- **红色节点的子节点必须是黑色。**
- **从任意节点到其所有后代叶节点的黑色节点数相同。**

这些性质确保了红黑树的高度平衡，从而保证了快速插入、删除和搜索操作。

#### 2.1.2 红黑树的插入和删除操作

**插入操作：**

1. 将新节点插入树中，初始为红色。
2. 如果新节点的父节点是黑色，则插入完成。
3. 如果新节点的父节点是红色，则需要重新着色和旋转树，以满足红黑树的性质。

**删除操作：**

1. 找到要删除的节点。
2. 如果该节点是叶子节点，则直接删除。
3. 如果该节点有一个子节点，则用该子节点替换它。
4. 如果该节点有两个子节点，则找到其后继节点（中序遍历中的下一个节点），用后继节点替换它，然后删除后继节点。
5. 删除后，需要重新着色和旋转树，以满足红黑树的性质。

### 2.2 AVL树

#### 2.2.1 AVL树的定义和性质

AVL树是一种自平衡二叉查找树，它满足以下性质：

- **对于每个节点，其左子树和右子树的高度差绝对值不超过 1。**
- **每个节点的高度等于其子树高度的最大值加 1。**

这些性质确保了 AVL 树的高度平衡，从而保证了快速插入、删除和搜索操作。

#### 2.2.2 AVL树的插入和删除操作

**插入操作：**

1. 将新节点插入树中。
2. 从新节点开始，向上遍历树，计算每个节点的平衡因子。
3. 如果某个节点的平衡因子绝对值大于 1，则需要重新着色和旋转树，以满足 AVL 树的性质。

**删除操作：**

1. 找到要删除的节点。
2. 如果该节点是叶子节点，则直接删除。
3. 如果该节点有一个子节点，则用该子节点替换它。
4. 如果该节点有两个子节点，则找到其后继节点（中序遍历中的下一个节点），用后继节点替换它，然后删除后继节点。
5. 删除后，需要重新着色和旋转树，以满足 AVL 树的性质。

# 3.1 数据结构

#### 3.1.1 字典和集合

自平衡树在数据结构中有着广泛的应用，其中一个重要的应用就是实现字典和集合。字典是一种键值对的数据结构，它允许用户通过键快速查找和检索值。集合是一种不包含重复元素的元素集合。

**字典**

自平衡树可以用来实现高效的字典，例如红黑树或AVL树。这些树保持平衡，确保在插入、删除或查找操作期间具有对数时间复杂度。使用自平衡树实现的字典具有以下优点：

- 快速插入：在红黑树或AVL树中插入一个元素的时间复杂度为 O(log n)，其中 n 是树中的元素数量。
- 快速查找：在红黑树或AVL树中查找一个元素的时间复杂度也为 O(log n)。
- 快速删除：在红黑树或AVL树中删除一个元素的时间复杂度为 O(log n)。

**集合**

自平衡树也可以用来实现高效的集合。集合可以通过使用字典来实现，其中键是集合中的元素，而值是布尔值（例如 True 或 False）。使用自平衡树实现的集合具有以下优点：

- 快速插入：在红黑树或AVL树中插入一个元素的时间复杂度为 O(log n)，其中 n 是集合中的元素数量。
- 快速查找：在红黑树或AVL树中查找一个元素的时间复杂度也为 O(log n)。
- 快速删除：在红黑树或AVL树中删除一个元素的时间复杂度为 O(log n)。

#### 3.1.2 优先级队列

优先级队列是一种数据结构，它允许用户存储元素并根据其优先级进行排序。自平衡树可以用来实现高效的优先级队列，例如红黑树或AVL树。

**优先级队列**

使用自平衡树实现的优先级队列具有以下优点：

- 快速插入：在红黑树或AVL树中插入一个元素的时间复杂度为 O(log n)，其中 n 是队列中的元素数量。
- 快速查找：在红黑树或AVL树中查找具有最高优先级的元素的时间复杂度为 O(1)。
- 快速删除：在红黑树或AVL树中删除具有最高优先级的元素的时间复杂度为 O(log n)。

自平衡树在优先级队列中的应用非常广泛，例如在调度算法、图算法和网络流算法中。

# 4. 自平衡树的性能分析**

**4.1 时间复杂度**

自平衡树的时间复杂度主要受其平衡操作的影响。平衡操作的目的是在插入或删除操作后保持树的平衡。

**4.1.1 插入和删除操作**

对于红黑树和AVL树，插入和删除操作的时间复杂度为O(log n)，其中n是树中的节点数。这是因为平衡操作最多需要对log n个节点进行旋转。

**代码块：**

def insert(self, key, value):
    # 插入新节点
    new_node = Node(key, value)
    self._insert(new_node)
    # 平衡树
    self._balance(new_node)

def _insert(self, node):
    if self.root is None:
        self.root = node
    else:
        self._insert_helper(node, self.root)

def _insert_helper(self, node, current_node):
    if node.key < current_node.key:
        if current_node.left is None:
            current_node.left = node
        else:
            self._insert_helper(node, current_node.left)
    else:
        if current_node.right is None:
            current_node.right = node
        else:
            self._insert_helper(node, current_node.right)

def _balance(self, node):
    # 检查是否需要平衡
    if self._is_unbalanced(node):
        # 执行旋转操作
        self._rotate(node)
        # 递归平衡父节点
        self._balance(node.parent)

**逻辑分析：**

* `insert()` 方法调用 `_insert()` 方法插入新节点，然后调用 `_balance()` 方法平衡树。
* `_insert()` 方法使用递归算法将新节点插入树中。
* `_balance()` 方法检查树是否平衡，如果需要，则执行旋转操作。
* 旋转操作将不平衡的子树重新排列为平衡的子树。

**4.1.2 搜索和范围查询**

自平衡树的搜索和范围查询操作的时间复杂度也为O(log n)。这是因为平衡操作确保了树的高度保持在log n的范围内。

**代码块：**

def search(self, key):
    # 从根节点开始搜索
    current_node = self.root
    # 循环直到找到节点或到达叶节点
    while current_node is not None:
        if key == current_node.key:
            return current_node
        elif key < current_node.key:
            current_node = current_node.left
        else:
            current_node = current_node.right
    # 未找到节点
    return None

def range_query(self, start, end):
    # 初始化结果列表
    result = []
    # 从根节点开始搜索
    current_node = self.root
    # 循环直到找到范围内的所有节点
    while current_node is not None:
        if start <= current_node.key <= end:
            result.append(current_node)
        elif current_node.key < start:
            current_node = current_node.right
        else:
            current_node = current_node.left
    # 返回结果列表
    return result

**逻辑分析：**

* `search()` 方法使用递归算法从根节点开始搜索树，直到找到节点或到达叶节点。
* `range_query()` 方法使用递归算法从根节点开始搜索树，将范围内所有节点添加到结果列表中。

**4.2 空间复杂度**

自平衡树的空间复杂度主要取决于树的高度。

**4.2.1 节点大小**

每个节点的大小与存储的键和值的大小成正比。对于红黑树和AVL树，每个节点通常存储一个键和一个值，因此节点的大小为O(1)。

**4.2.2 树的高度**

自平衡树的高度保持在log n的范围内，其中n是树中的节点数。这是因为平衡操作确保了树不会变得过于不平衡。

**表格：**

| 树类型 | 节点大小 | 树的高度 | 空间复杂度 |
|---|---|---|---|
| 红黑树 | O(1) | O(log n) | O(n log n) |
| AVL树 | O(1) | O(log n) | O(n log n) |

# 5. 自平衡树的扩展

### 5.1 B树

#### 5.1.1 B树的定义和性质

B树是一种平衡的多路搜索树，其特点是每个节点都可以包含多个子节点。B树的定义如下：

- **阶数**：B树的阶数m定义了每个节点最多可以包含多少个子节点。
- **根节点**：B树的根节点至少包含两个子节点。
- **内部节点**：内部节点包含m-1个子节点和m个键值对。
- **叶子节点**：叶子节点不包含子节点，只包含m个键值对。
- **所有叶子节点都在同一层**：B树的所有叶子节点都位于同一层，这确保了B树的平衡性。

#### 5.1.2 B树的插入和删除操作

**插入操作**

1. 从根节点开始，找到要插入键值对的子节点。
2. 如果子节点已满，则将其分裂为两个子节点，并将要插入的键值对插入到其中一个子节点中。
3. 继续递归地将要插入的键值对插入到子节点中，直到找到一个未满的子节点。
4. 将要插入的键值对插入到未满的子节点中，并调整父节点的键值对。

**删除操作**

1. 从根节点开始，找到要删除的键值对的子节点。
2. 如果子节点中包含要删除的键值对，则将其删除。
3. 如果子节点中不包含要删除的键值对，则递归地将其子节点中查找要删除的键值对。
4. 如果子节点删除键值对后变为空，则将其与相邻的子节点合并。
5. 继续递归地将要删除的键值对从子节点中删除，直到到达根节点。

### 5.2 B+树

#### 5.2.1 B+树的定义和性质

B+树是一种平衡的多路搜索树，其特点是所有数据都存储在叶子节点中。B+树的定义如下：

- **阶数**：B+树的阶数m定义了每个节点最多可以包含多少个子节点。
- **根节点**：B+树的根节点至少包含两个子节点。
- **内部节点**：内部节点包含m-1个子节点和m个键值对。
- **叶子节点**：叶子节点包含m个键值对，并且所有叶子节点都链接在一起。
- **所有叶子节点都在同一层**：B+树的所有叶子节点都位于同一层，这确保了B+树的平衡性。

#### 5.2.2 B+树的插入和删除操作

**插入操作**

1. 从根节点开始，找到要插入键值对的子节点。
2. 如果子节点已满，则将其分裂为两个子节点，并将要插入的键值对插入到其中一个子节点中。
3. 继续递归地将要插入的键值对插入到子节点中，直到找到一个未满的子节点。
4. 将要插入的键值对插入到未满的子节点中，并调整父节点的键值对。

**删除操作**

1. 从根节点开始，找到要删除的键值对的子节点。
2. 如果子节点中包含要删除的键值对，则将其删除。
3. 如果子节点中不包含要删除的键值对，则递归地将其子节点中查找要删除的键值对。
4. 如果子节点删除键值对后变为空，则将其与相邻的子节点合并。
5. 继续递归地将要删除的键值对从子节点中删除，直到到达根节点。

# 6. 自平衡树在实际应用中的案例

自平衡树在实际应用中有着广泛的应用，以下列举几个常见的案例：

### 6.1 数据库索引

在数据库中，索引是一种数据结构，用于快速查找和检索数据。自平衡树可以作为索引的数据结构，因为它具有快速查找和插入操作的特点。通过使用自平衡树作为索引，可以显著提高数据库的查询性能。

### 6.2 文件系统

在文件系统中，自平衡树可以用来组织和管理文件和目录。通过使用自平衡树，可以快速查找文件和目录，并高效地进行文件和目录的插入和删除操作。

### 6.3 内存管理

在内存管理中，自平衡树可以用来管理内存分配和释放。通过使用自平衡树，可以快速找到可用内存块，并高效地分配和释放内存块。