加速图像处理任务：DCT算法的并行化技术

# 1. 图像处理概述

图像处理是计算机科学的一个分支，它涉及到对数字图像进行操作和分析。图像处理技术在各种应用中至关重要，包括医学成像、遥感、工业自动化和娱乐。

图像处理算法通常涉及到对图像像素进行各种操作，例如转换、滤波和增强。其中最常见的图像处理算法之一是离散余弦变换 (DCT)。DCT 是一种将图像从空间域转换为频率域的数学变换。它在图像压缩、图像增强和图像分析等应用中发挥着关键作用。

在本章中，我们将探讨图像处理的基础知识，重点关注 DCT 算法及其在图像处理中的应用。我们将深入研究 DCT 的数学原理、变体和应用，为后续章节中 DCT 算法的并行化技术奠定基础。

# 2. DCT算法的理论基础

### 2.1 DCT的数学原理

离散余弦变换（DCT）是一种线性变换，用于将时域信号（例如图像）转换为频域信号（例如频谱）。DCT的数学原理基于余弦函数的正交性，即：

cos(nπx/N) cos(mπx/N) dx = 0,  n ≠ m

其中，N为信号长度。

DCT的公式为：

F(u) = α(u) ∑[n=0}^{N-1} f(n) cos(πun/2N),  u = 0, 1, ..., N-1

其中，α(u)为归一化系数，f(n)为时域信号，F(u)为频域信号。

### 2.2 DCT的变体和应用

DCT有多种变体，包括：

- **类型I DCT（DCT-I）：**用于处理实数信号，且边界条件为f(0)=f(N-1)。
- **类型II DCT（DCT-II）：**用于处理实数信号，且边界条件为f(0)=f(N-1)=0。
- **类型III DCT（DCT-III）：**用于处理实数信号，且边界条件为f'(0)=f'(N-1)=0。
- **类型IV DCT（DCT-IV）：**用于处理复数信号，且边界条件为f(0)=f*(N-1)。

DCT广泛应用于图像处理、视频编码、音频压缩等领域。在图像处理中，DCT可以用于图像降噪、图像压缩、图像增强等任务。在视频编码中，DCT用于将视频帧分解为频域系数，从而实现视频压缩。在音频压缩中，DCT用于将音频信号分解为频域系数，从而实现音频压缩。

**代码块：DCT-II的Python实现**

import numpy as np

def dct2(f):
    """
    计算图像的DCT-II变换。

    参数：
        f：输入图像，形状为(M, N)。

    返回：
        F：DCT-II变换后的图像，形状为(M, N)。
    """

    M, N = f.shape
    F = np.zeros((M, N))

    for u in range(M):
        for v in range(N):
            α = 1 / np.sqrt(2 * N) if u == 0 else 1 / np.sqrt(N)
            F[u, v] = α * ∑[n=0}^{M-1} ∑[m=0}^{N-1} f[n, m] * cos(πun/2M) * cos(πvm/2N)

    return F

**逻辑分析：**

该代码块实现了DCT-II变换，它遍历输入图像的每个像素，并计算其DCT-II系数。α系数用于归一化变换结果。

# 3. DCT算法的并行化技术**

### 3.1 并行化策略概述

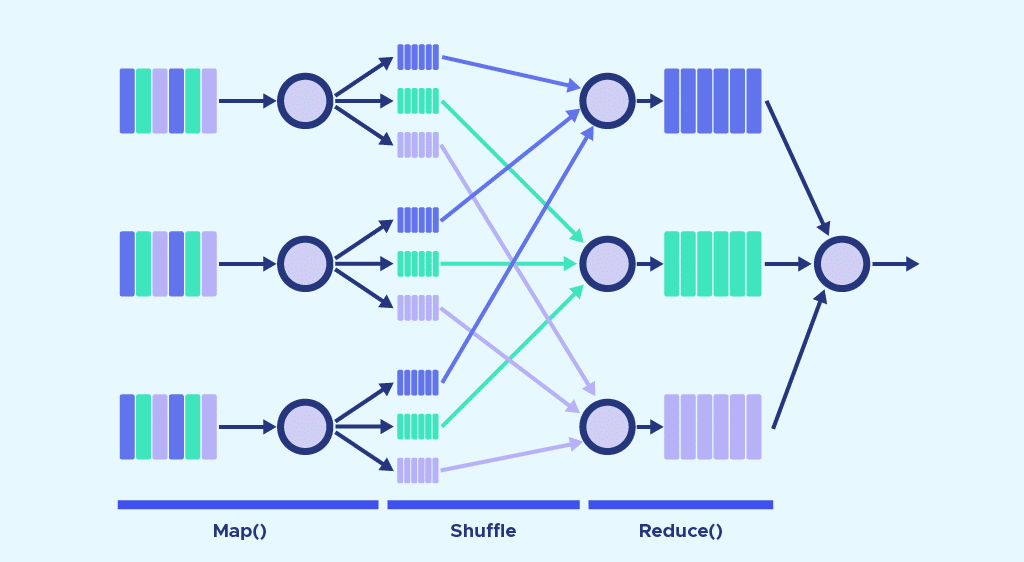
DCT算法并行化的核心思想是将计算任务分解成多个子任务，并分配给多个处理单元同时执行。并行化策略的选择取决于算法的特性、可用的硬件资源以及性能要求。

**并行化类型：**

- **数据并行：**将数据块分配给不同的处理单元，每个处理单元独立处理自己的数据块。
- **任务并行：**将算法中的不同任务分配给不同的处理单元，每个处理单元执行特定的任务。

**并行化粒度：**

- **粗粒度并行：**将算法分解成较大的任务，每个任务需要较长时间才能完成。
- **细粒度并行：**将算法分解成较小的任务，每个任务需要较短的时间才能完成。

### 3.2 基于多核处理器的并行化

多核处理器具有多个处理核心，可用于