召回率在A_B测试中的作用

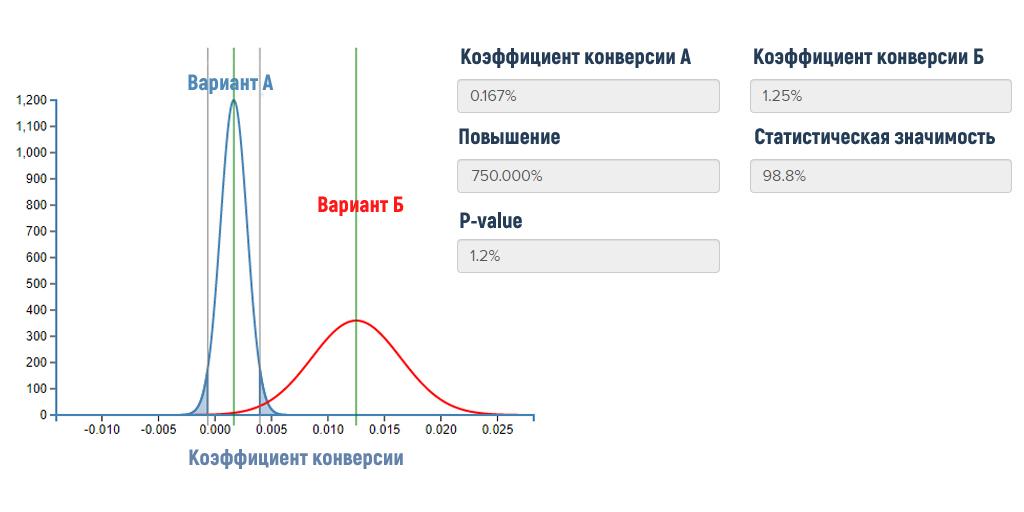
# 1. A_B测试基础与召回率概念

## 1.1 A_B测试简介
A_B测试，又称分裂测试，是一种在用户界面上比较两种或多种版本，以确定哪些改变能提高特定关键性能指标（KPI）的实验方法。这一测试方法常用于网站、移动应用、产品设计与营销策略的优化，通过向不同用户群体展示不同的版本，来测试哪个版本的性能更优。

## 1.2 召回率概念引入
在A_B测试中，我们经常遇到衡量实验有效性的问题，其中一个关键指标就是召回率。召回率（Recall），在信息检索领域，是指在所有相关实例中，系统正确识别的实例所占的比例。它衡量的是模型对相关数据的捕捉能力。例如，在A_B测试中，如果改动版A相对于控制版B在目标用户中提高了某个行为发生的次数，则召回率能帮助我们量化这种提升。要深入了解召回率如何在A_B测试中发挥作用，接下来章节将展开对其理论基础和实践应用的详细探讨。

# 2. 召回率在A_B测试中的理论基础

## 2.1 A_B测试的统计学原理
### 2.1.1 假设检验与显著性水平

在统计学中，假设检验是一种用于检验某个假设是否成立的方法。A_B测试通过假设检验，对两种不同版本的网页或产品特性进行比较，判断它们之间是否存在显著差异。

在进行假设检验时，我们通常设定一个原假设（H0），即没有差异（例如，两个版本的转换率相等），以及一个备择假设（H1），即存在差异（例如，新版本的转换率更高或更低）。通过收集数据并应用适当的统计测试，我们计算出p值。p值是观察到的数据或更极端结果在原假设成立的情况下出现的概率。如果p值低于某个阈值（称为显著性水平，通常为0.05或0.01），则拒绝原假设，接受备择假设。

graph TD
A[开始A_B测试] --> B[设定原假设和备择假设]
B --> C[收集数据]
C --> D[计算p值]
D --> E{p值是否小于显著性水平}
E -->|是| F[拒绝原假设]
E -->|否| G[不能拒绝原假设]

### 2.1.2 统计功效与功效曲线

统计功效（也称为测试的功效或功效度）是指在备择假设实际上为真的情况下，正确拒绝原假设的概率。统计功效越大，犯第二类错误（错误地接受原假设）的机会就越小。

为了确定一个A_B测试具有足够的功效，我们需要进行功效分析。功效曲线展示了不同样本大小下测试的功效，它帮助我们理解在不同的效应大小下，测试结果达到统计显著性的可能性。通常，功效曲线越高、越陡峭，表明实验设计的统计效能越强。

graph LR
A[开始A_B测试] --> B[设定原假设和备择假设]
B --> C[选择显著性水平]
C --> D[计算统计功效]
D --> E[绘制功效曲线]

## 2.2 召回率的定义与计算方法
### 2.2.1 召回率的基本公式

在信息检索、机器学习评估以及A_B测试中，召回率（Recall）是评估模型性能的一个关键指标，它衡量的是模型识别出相关实例的比例。在二分类问题中，召回率的计算公式为：

Recall = \frac{True Positive}{True Positive + False Negative}

其中，True Positive（TP）是指模型正确识别为正例的数量，False Negative（FN）是指实际上为正例却被模型识别为负例的数量。召回率关注的是模型在实际正例中的识别能力，召回率越高表示模型漏掉的正例越少。

### 2.2.2 不同场景下的召回率计算实例

为了更好地理解召回率的计算和应用，我们来看一个具体的例子。假设在一个A_B测试中，我们比较两个网页版本A和B，目标是提高用户注册的数量。在这个场景中，注册被视为“正例”，未注册则是“负例”。

假设版本A有200名访问者，其中100名注册（TP），还有100名未注册但本应注册（FN）。版本B有250名访问者，其中120名注册（TP），并且有80名未注册但本应注册（FN）。版本B的召回率计算如下：

Recall_{B} = \frac{120}{120 + 80} = \frac{120}{200} = 0.60

版本A的召回率计算如下：

Recall_{A} = \frac{100}{100 + 100} = \frac{100}{200} = 0.50

在这个例子中，版本B的召回率更高，意味着它在吸引用户注册方面做得更好。这个计算帮助我们理解了召回率在实验中的应用和重要性。

## 2.3 召回率与其他指标的关系
### 2.3.1 召回率与精确度的权衡

召回率和精确度（Precision）是评估分类模型性能的两个常用指标。精确度关注的是模型预测为正例中实际为正例的比例，其计算公式为：

Precision = \frac{True Positive}{True Positive + False Positive}

在实际应用中，召回率和精确度往往存在一种权衡关系。提高召回率通常会降低精确度，反之亦然。一个模型可能识别出大部分正例（高召回率），但也会错误地识别出一些负例（低精确度）。同样，一个高精确度模型可能错过许多实际为正的实例（低召回率）。

这种权衡关系要求我们在设计A_B测试时，根据业务目标和模型用途来平衡这两个指标。例如，在需要尽量减少漏检的情况下，我们可能更倾向于提高召回率，即便这会导致一些错误的预测。

### 2.3.2 召回率与F1分数的综合考量

F1分数是召回率和精确度的调和平均数，它提供了一个单一的数值来综合考虑这两个指标。F1分数的计算公式为：

F1 = 2 \times \frac{Recall \times Precision}{Recall + Precision}

F1分数的取值范围在0和1之间，数值越高表示模型在召回率和精确度上的表现越好。F1分数特别适用于那些正负样本分布不均或者更倾向于避免假正例或假负例的场景。

在实际应用中，我们通过调整分类阈值来平衡召回率和精确度，以达到理想的F1分数。例如，如果一个模型在精确度上有过高的表现，但召回率低，我们可以通过降低分类阈值来增加召回率，同时保持F1分数的平衡。

graph TD
A[开始A_B测试] --