节点组抗矩阵的动态特性分析：深入理解和应用


# 摘要
节点组抗矩阵是一种数学模型，用于描述和分析系统中节点组的抗干扰能力。本文首先定义了节点组抗矩阵的基本概念，然后深入探讨了其理论基础，包括数学表述、物理意义、分类和性质。接下来，本文详细介绍了节点组抗矩阵的计算方法、动态模拟技术和在不同领域中的应用实例。此外，本文还探讨了节点组抗矩阵的优化与改进策略，并展望了节点组抗矩阵在前沿研究中的应用趋势以及未来可能面临的挑战和应对策略。本文旨在为研究人员和工程师提供全面的指导和参考，以更有效地应用节点组抗矩阵解决实际问题。

# 关键字
节点组抗矩阵；理论基础；动态模拟；优化算法；综合应用；未来趋势

参考资源链接：[节点导纳矩阵与节点组抗矩阵小结](https://wenku.csdn.net/doc/6412b750be7fbd1778d49db7?spm=1055.2635.3001.10343)
# 1. 节点组抗矩阵的定义与基本概念

## 1.1 节点组抗矩阵的定义
节点组抗矩阵是一个在多个学科领域中起着关键作用的数学概念。它通常用于描述系统的结构特性，是分析系统稳定性和动态行为的重要工具。简而言之，节点组抗矩阵可以看作是一个系统内部节点间相互作用的量化表示。

## 1.2 基本术语解释
在深入探讨节点组抗矩阵之前，我们必须了解一些基础概念：
- **节点**：系统中可以被单独识别和分析的单元。
- **抗性**：表示节点之间抵抗变化或干扰的能力。
- **矩阵**：一种数学工具，用于组织和处理数值信息。

## 1.3 节点组抗矩阵的应用
节点组抗矩阵在许多领域都有广泛的应用，例如：
- **网络分析**：在网络的稳定性和鲁棒性分析中，节点组抗矩阵可以揭示网络连接结构的特点。
- **系统控制**：在控制理论中，用于设计控制器和预测系统响应。
- **电路分析**：在电子电路设计中，节点组抗矩阵有助于分析电路的行为和优化电路布局。

在下一章节中，我们将深入探讨节点组抗矩阵的理论基础，包括其数学表述、物理意义以及分类和性质。这将为我们后续章节中对节点组抗矩阵的计算、优化和应用分析打下坚实的基础。

# 2. 节点组抗矩阵的理论基础

## 2.1 节点组抗矩阵的数学表述

### 2.1.1 线性代数中的矩阵理论基础

线性代数作为数学的一个分支，它在描述和解决线性关系问题中扮演着核心角色。在探讨节点组抗矩阵之前，有必要理解线性代数中矩阵的基础知识。矩阵是由数字或表达式组成的矩形阵列，其主要运算包括加法、数乘、乘法等。

矩阵的加法遵循逐元素相加的规则，数乘则是对矩阵中的每个元素进行乘法操作，而乘法则稍微复杂，需要遵循行列数一致的原则。线性变换、解线性方程组等场景中，矩阵的乘法都有其独特且不可替代的作用。

例如，线性方程组可以表示为 AX = B，其中A是系数矩阵，X是未知变量矩阵，B是常数项矩阵。在许多实际问题中，如物理学、工程学、经济学等，都会出现类似的线性关系，需要通过矩阵运算来分析和解决。

### 2.1.2 节点组抗矩阵的特征值与特征向量

节点组抗矩阵是一种特定的矩阵形式，它在描述系统节点间相互作用时具有重要应用。对节点组抗矩阵进行特征值与特征向量的分析，有助于了解系统在某种变换下的基本特性。

特征值和特征向量是线性代数中的重要概念。对于一个n×n的矩阵A，如果存在非零向量v和标量λ，使得Av = λv，则称λ为A的一个特征值，v为对应的特征向量。特征值描述了矩阵变换后的某个方向上的伸缩因子，而特征向量则是这个变换方向的基向量。

计算节点组抗矩阵的特征值和特征向量可以使用数值方法，例如幂法、QR算法等。在实际应用中，特征值分析可以用来评估系统的稳定性，判断系统状态是否会随着时间发散或收敛到某个平衡点。

## 2.2 节点组抗矩阵的物理意义

### 2.2.1 系统稳定性与矩阵特征值的关系

稳定性分析是控制理论及系统动力学中的一个基本问题。稳定性通常指一个系统在受到扰动后，是否能够回到平衡状态或者保持某种状态不变。

在系统稳定性分析中，节点组抗矩阵的特征值发挥着关键作用。若矩阵的所有特征值的实部都是负的，系统则是稳定的。反之，若至少有一个特征值的实部为正，则系统不稳定。

例如，在电子电路的稳定性分析中，节点组抗矩阵的特征值可以指示电路是否会进入振荡状态。如果所有的特征值都在左半平面（实部小于零），那么电路在理论上不会出现无限制的振荡。

### 2.2.2 节点组抗矩阵在动态系统中的作用

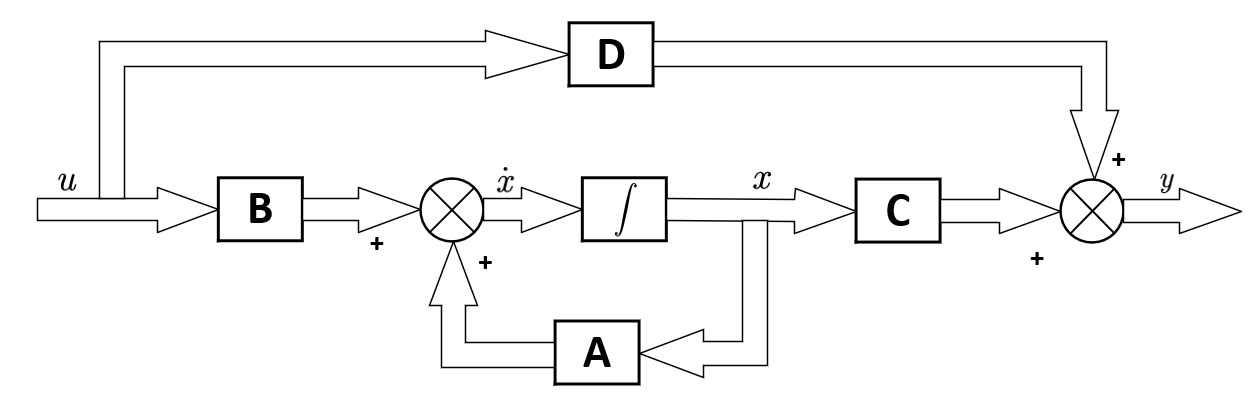
在动态系统中，节点组抗矩阵描述了系统各节点状态变化之间的相互关系。动态系统一般可以用线性时不变系统或线性时变系统来描述，其中线性时不变系统的动态行为可以用常系数微分方程或差分方程表示。

节点组抗矩阵中的每个元素可以是常数或者时间的函数，它直接决定了系统随时间变化的动态特性。通过分析节点组抗矩阵，可以预测系统对初始条件或外在扰动的反应，从而找到控制策略以达到期望的系统行为。

例如，在机械系统中，节点组抗矩阵可以用来分析多自由度系统中质量、阻尼和刚度之间的动态相互作用。通过这样的分析，工程师可以设计出更加稳定可靠的机械结构。

## 2.3 节点组抗矩阵的分类与性质

### 2.3.1 不同类型节点组抗矩阵的特点

节点组抗矩阵根据其物理背景和数学性质可以划分为不同类型。例如，对称矩阵、非对称矩阵、稀疏矩阵、正定矩阵等。每种类型的矩阵在系统分析中有其独特的特点和适用场景。

对称矩阵的元素满足A = A^T，其中A^T是矩阵A的转置。对于这类矩阵，其特征值都是实数，特征向量之间互相正交，便于进行进一步的数学处理。在物理系统中，对称性往往反映了某种物理对称性或守恒性。

非对称矩阵不存在A = A^T的性质，它们可以描述具有方向性或非平衡状态的物理系统。非对称矩阵的特征值可能是复数，这表示系统可能会有振荡行为。

稀疏矩阵在系统分析中常常涉及，因为它们的大部分元素都是零，这对于计算资源的消耗有显著的降低效果。在很多实际问题中，系统的相互作用通常只在有限的范围内存在，因此可以有效地利用稀疏矩阵进行建模。

### 2.3.2 矩阵性质对动态特性的影响

矩阵的性质决定了系统动态特性的很多方面。例如，矩阵的谱半径（最大的特征值绝对值）影响着系统的时间响应特性。谱半径越大，系统对初始条件的敏感度越高，可能意味着更长的调整时间。

另一个重要的性质是矩阵的条件数，它衡量了矩阵在数值计算中的稳定性。条件数越小，矩阵越稳定，反之则越不稳定。对于数值计算来说，不稳定的矩阵可能导致严重的误差扩散。

矩阵的可逆性也是影响动态特性的因素之一。如果矩阵可逆，那么系统将具有确定的唯一解。反之，如果矩阵奇异（不可逆），则系统的某些行为可能是不确定的，或者存在多重解。

通过深入理解矩阵性质对动态特性的影响，我们可以更有效地设计和控制系统，避免不稳定和不可预测的行为。例如，在飞行器的稳定性分析中，通过调整系统的节点组抗矩阵可以实现对飞行器动态行为的精确控制。

### 表格展示不同矩阵类型及其特点

| 矩阵类型 | 特点 | 物理意义 | 数学性质 |
|-----------|--------|------------|------------|
| 对称矩阵 | A = A^T | 反映系统对称性 | 特征值均为实数，特征向量正