【AI高手】：掌握这些技巧，A*算法解决8数码问题游刃有余


# 摘要
A*算法是计算机科学中广泛使用的一种启发式搜索算法，尤其在路径查找和问题求解领域表现出色。本文首先概述了A*算法的基本概念，随后深入探讨了其理论基础，包括搜索算法的分类和评价指标，启发式搜索的原理以及评估函数的设计。通过结合著名的8数码问题，文章详细介绍了A*算法的实际操作流程、编码前的准备、实现步骤以及优化策略。在应用实例部分，文章通过具体问题的实例化和算法的实现细节，提供了深入的案例分析和问题解决方法。最后，本文展望了A*算法的进阶拓展，比较了与其他搜索算法的差异，并对其理论深度和未来应用趋势进行了探讨，为读者提供了进一步学习和研究的资源。

# 关键字
A*算法；搜索算法；启发式搜索；评估函数；8数码问题；算法优化

参考资源链接：[A*算法解决8数码问题详解及实验报告](https://wenku.csdn.net/doc/3xbcks9m4a?spm=1055.2635.3001.10343)
# 1. A*算法概述

## 简介
A*（A-Star）算法是一种启发式搜索算法，广泛应用于路径规划和图遍历。它结合了最佳优先搜索和最短路径搜索的特点，通过评估函数来优化搜索过程，有效减少了不必要的节点探索，从而提高了搜索效率。

## 发展历史
该算法最初由Peter Hart, Nils Nilsson 和 Bertram Raphael 在1968年的研究报告中提出，经过数十年的发展，已成为解决路径问题的重要工具，尤其在游戏设计、机器人导航和网络路由等领域得到广泛应用。

## 应用领域
由于A*算法的灵活性和高效性，它不仅被应用于8数码问题等经典的路径搜索问题，还可以拓展至物流配送、网络拓扑设计等多种实际场景，通过算法优化来适应不同领域的问题需求。

# 2. A*算法理论基础

## 2.1 搜索算法简介

### 2.1.1 搜索算法的分类

搜索算法可以分为两类：无信息搜索算法（Uninformed Search）和有信息搜索算法（Informed Search）。

**无信息搜索算法**不使用问题域的特定知识，不考虑搜索路径的成本。主要的无信息搜索算法包括：

- **深度优先搜索（DFS）**：按照深度优先的策略遍历节点，先深入再回溯。
- **广度优先搜索（BFS）**：按照宽度优先的策略遍历节点，逐层扩展。
- **双向搜索**：从起始点和目标点同时进行搜索，减少搜索空间。
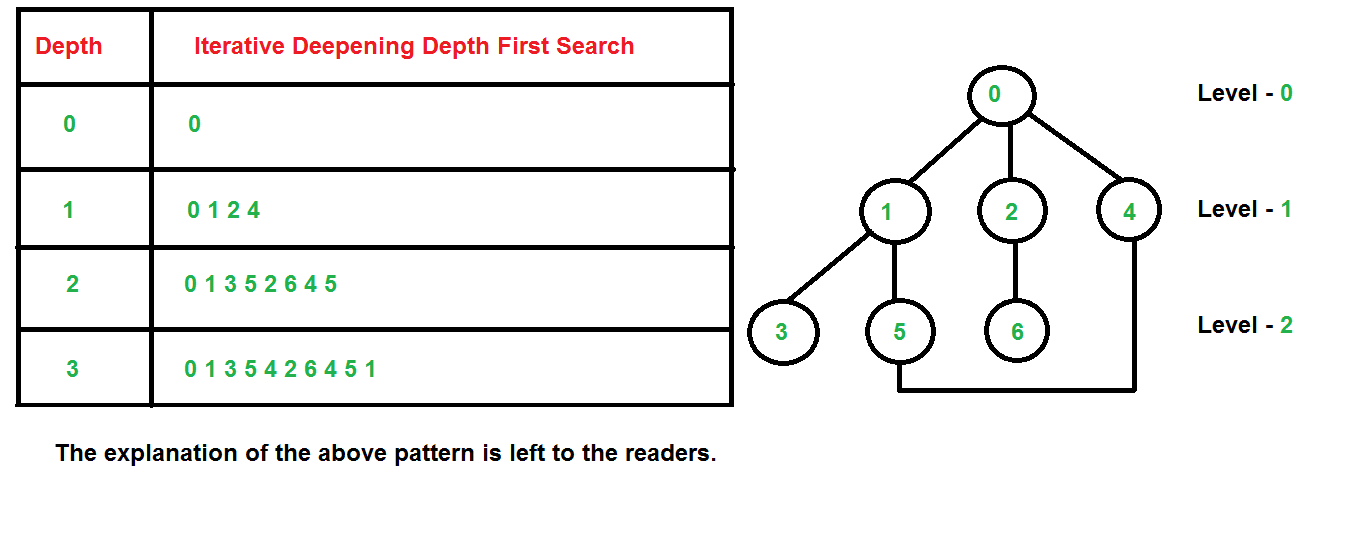
- **迭代加深搜索**：结合了DFS和BFS的特点，先进行浅层搜索，再逐渐深入。

**有信息搜索算法**，也就是启发式搜索，使用问题域的知识来指导搜索过程，更加高效。主要的有信息搜索算法包括：

- **贪婪最佳优先搜索（Greedy Best-First Search）**：根据启发式函数优先扩展看起来最接近目标的节点。
- **A*算法**：结合了BFS和贪婪最佳优先搜索的优点，通过评估函数选择扩展节点。

### 2.1.2 搜索算法的评价指标

搜索算法的评价指标主要涉及以下几个方面：

- **完备性**：算法是否总是能找到一个解，如果存在解的话。
- **最优性**：是否能找到最短路径的解。
- **时间复杂度**：找到解所需的时间。
- **空间复杂度**：存储搜索空间所需的空间。

## 2.2 A*算法的原理

### 2.2.1 启发式搜索的概念

启发式搜索是一种以问题特定知识为基础来指导搜索过程的算法，它可以大大减少搜索空间，提高搜索效率。其核心是使用启发式函数（h(x)），它估计从当前节点到目标节点的最佳路径成本。

### 2.2.2 评估函数的设计

A*算法的评估函数通常表示为：f(n) = g(n) + h(n)，其中：

- f(n) 是节点n的总估计成本。
- g(n) 是从起始节点到节点n的实际成本。
- h(n) 是从节点n到目标节点的启发式估计成本。

评估函数设计的关键在于选择合适的启发式函数。理想情况下，h(n)应满足两个条件：

- **可采纳性**：h(n)不会过高估计实际成本。
- **一致性**（也称为单调性）：对于任何节点n和任意后继节点n'，若n'是通过一步操作从n可达的，那么h(n) ≤ cost(n, n') + h(n')。

## 2.3 A*算法与8数码问题

### 2.3.1 8数码问题的定义

8数码问题是一个经典的搜索问题，它包含一个3x3的网格，其中8个格子被数字1到8填满，一个格子为空。目标是通过滑动格子来达到一个预定的目标状态。

### 2.3.2 A*算法在8数码问题中的应用

A*算法在8数码问题中的应用非常有效，因为可以通过设计合适的启发式函数来估算从当前状态到目标状态的距离。例如，可以使用不在位的数码数或者不在位数码与目标位置之间的曼哈顿距离作为启发式函数。

在8数码问题中，A*算法通过评估函数选择路径，将可能的解决方案按照成本从低到高排列，并扩展成本最低的节点，直到找到解决方案或确定没有解决方案为止。

### 章节结尾

在这部分中，我们了解了A*算法的理论基础，包括搜索算法的分类、A*算法的原理，以及它如何应用于解决8数码问题。接下来，我们将探讨A*算法的实践操作和如何在具体问题中应用这一强大的搜索工具。

# 3. A*算法实践操作

## 3.1 算法编码前的准备

在着手编写A*算法代码之前，我们首先需要确定适合的编程语言和选择合适的开发工具。A*算法本身是一种思想较为独立的算法，可以使用多种编程语言实现，如Pyth