【Origin FFT：让频谱分析更简单】：从入门到专家的全面指南


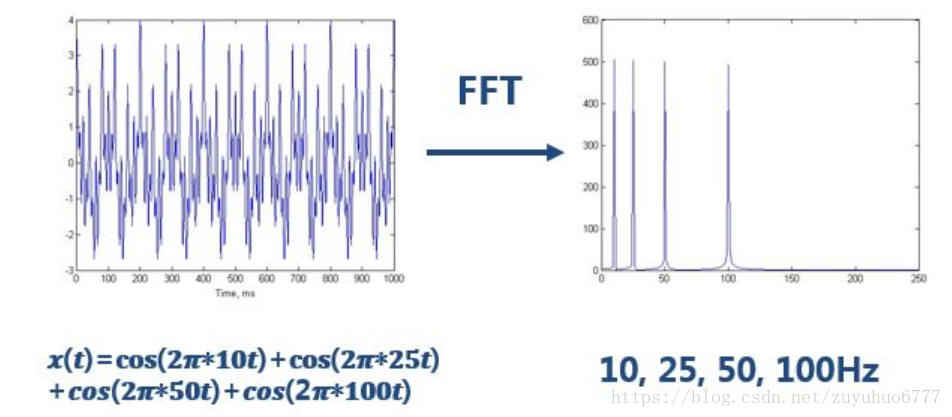
参考资源链接：[Origin入门详解：快速傅里叶变换与图表数据分析](https://wenku.csdn.net/doc/61vro5yysf?spm=1055.2635.3001.10343)
# 1. Origin FFT概述及应用背景

在数字化时代，频谱分析已成为工程、科学以及数据分析中不可或缺的一部分。Origin FFT（快速傅里叶变换）是Origin软件中一种强大的数学工具，用于分析各种信号和数据集。作为一种变换技术，FFT能够在频域中分解时域信号，揭示数据的频率组成。这种方法广泛应用于通信、音频处理、生物医学工程以及物理科学等众多领域。

Origin FFT不仅提供了快速分析复杂信号频谱的能力，也使得数据处理和可视化变得更加高效。本章将简要介绍FFT的基本概念、起源和发展，以及它在现代应用中的重要性。

## 1.1 应用背景和重要性

FFT作为数字信号处理的核心算法之一，极大地提高了频谱分析的速度和效率。与传统傅里叶变换相比，FFT可以将计算量减少至O(N log N)，这对于处理大量数据集尤为重要。比如，在无线通信领域，FFT使得高速数据传输成为可能；在音频工程中，FFT用于分析音乐的频谱特征，帮助优化声音效果。本章将探讨FFT在不同领域的应用背景及其重要性。

# 2. 理解频谱分析基础

频谱分析是信号处理领域中的一个基本且重要的工具。通过频谱分析，我们能够将信号从时域转换到频域，从而获取信号的频率成分、幅度以及相位等重要信息。本章我们将探讨频谱分析的理论基础，了解傅里叶变换在这一过程中的作用，并深入学习FFT算法如何优化这一过程。

## 2.1 频谱分析理论基础

### 2.1.1 信号的傅里叶变换

傅里叶变换是一种将时域中的信号转换为频域表示的方法。它由法国数学家让-巴普蒂斯特·约瑟夫·傅里叶提出，以他的名字命名。傅里叶变换的核心思想在于任何周期性信号都可以分解为一系列的正弦波和余弦波的叠加。

对于离散信号，离散傅里叶变换（DFT）能够提供信号频率成分的离散集合。从数学的角度来看，DFT将时域信号表示为一系列复指数函数的和。

X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-\frac{i2\pi kn}{N}}

其中，`X[k]`是频域中的复数表示，`x[n]`是时域中的信号样本，`N`是样本总数，`k`是频率索引（从0到N-1）。

### 2.1.2 频域与时域的关系

频域与时域的关系是互补的。时域中的信号反映了某个时间段内的变化，而频域中的信号揭示了不同频率分量的组成。这种转换对于理解信号的本质至关重要。

在频域中，我们可以清晰地看到各个频率分量的幅值和相位，这对于分析信号的特性非常有用。例如，在通信系统中，频谱分析可以帮助我们了解带宽需求，进行信号过滤和调制解调等。

## 2.2 FFT算法原理

### 2.2.1 离散傅里叶变换(DFT)

虽然DFT是一种强大的工具，但它的计算成本较高，特别是对于长序列数据。DFT的计算复杂度随着序列长度的增加而呈二次方增长。对于N个样本点的信号，DFT需要进行N^2次复数乘法，这对于大量数据来说非常耗时。

### 2.2.2 快速傅里叶变换(FFT)的优化

快速傅里叶变换（FFT）由J.W. Cooley和J.W. Tukey在1965年提出，它极大地减少了DFT的计算量。FFT的出现使得实施数字信号处理成为可能，并且对许多工程和科学领域产生了深远影响。

FFT算法利用了信号样本之间的周期性和对称性属性，通过分治策略将DFT分解成更小的DFTs来执行。这大大减少了需要执行的复数乘法次数，将复杂度降低至NlogN级别。

X[k] = Σ (x[n] * W_N^(kn))

其中，`W_N`是旋转因子，其形式为：

W_N = e^(-i*2π/N)

## 2.3 频谱分析在不同领域的应用

### 2.3.1 通信领域的应用

频谱分析在通信领域发挥着重要作用。在无线通信中，频谱分析帮助我们确定信号的载波频率、带宽以及可能的干扰源。工程师可以利用频谱分析来设计滤波器，优化频谱资源分配，进行信号调制和解调。

### 2.3.2 音频分析和处理

在音频分析中，频谱分析可以揭示音频信号的频率组成，这对于音乐制作、语音识别和噪声消除等应用至关重要。通过分析音频信号的频谱，我们可以进行音质改进，甚至在某些情况下，能够分析出声音的来源和特性。

频谱分析不仅可以用于技术分析，还在艺术创作和人机交互中提供了新的可能性。艺术家们利用频谱可视化技术创造出引人入胜的声音视觉作品，交互式设计允许用户通过声音直接控制和影响视觉效果。

以上内容覆盖了频谱分析的理论基础，包括信号的傅里叶变换、频域与时域的关系、FFT算法原理，以及频谱分析在不同领域的应用。在下一章节中，我们将深入到具体的软件工具中，探讨如何在Origin中使用FFT工具，并进一步了解其功能和参数设置。

# 3. Origin FFT功能详解

在数字信号处理中，Origin软件为科研工作者提供了一个方便直观的平台来进行频谱分析，尤其是在快速傅里叶变换（FFT）的应用方面。FFT是一种高效计算离散傅里叶变换（DFT）及其逆变换的算法，它极大地降低了计算量，是现代数字信号处理不可或缺的工具之一。本章节将详细介绍Origin软件中FFT的界面工具，参数设置，以及如何与其他软件进行比较分析。

## 3.1 Origin软件界面及工具介绍

### 3.1.1 Origin软件布局和菜单导航

Origin软件的界面布局对于新手和经验丰富的用户来说都相对直观易用。从上至下，软件的界面分为标题栏、菜单栏、工具栏、工作区和状态栏