【软件集成实战】：如何将NURBS曲线插值功能集成到您的应用中


# 摘要
NURBS曲线插值是计算机图形学和几何建模中的核心内容，本文旨在系统介绍NURBS曲线插值的基础知识、理论分析、软件集成实践以及应用案例。首先，通过理论分析探讨NURBS曲线插值的数学基础和算法实现，强调了插值与逼近的区别及数学模型构建的重要性。其次，阐述了NURBS曲线插值在软件集成中的实现步骤、测试与优化过程。文中进一步通过具体的应用案例分析，展示了NURBS曲线插值在3D建模、动画制作和工业设计中的实际应用和效果。最后，讨论了NURBS曲线插值的高级特性及未来发展展望，并提供了相关学习资源与技术支持的信息。本文为相关领域学者和技术人员提供了全面深入的理解和应用指南。
# 关键字
NURBS曲线插值；数学基础；算法探究；软件集成；性能考量；应用案例；高级特性；未来展望；学习资源；技术支持

参考资源链接：[NURBS曲线插值：Matlab编程实现与反求控制点解析](https://wenku.csdn.net/doc/qgjdzt8nba?spm=1055.2635.3001.10343)
# 1. NURBS曲线插值基础知识

在计算机图形学和几何建模领域，非均匀有理B样条（NURBS）是一种非常重要的曲线与曲面表示方法。本章节首先介绍NURBS曲线插值的基本概念，为读者提供必要的理论基础。

## 1.1 NURBS曲线概述

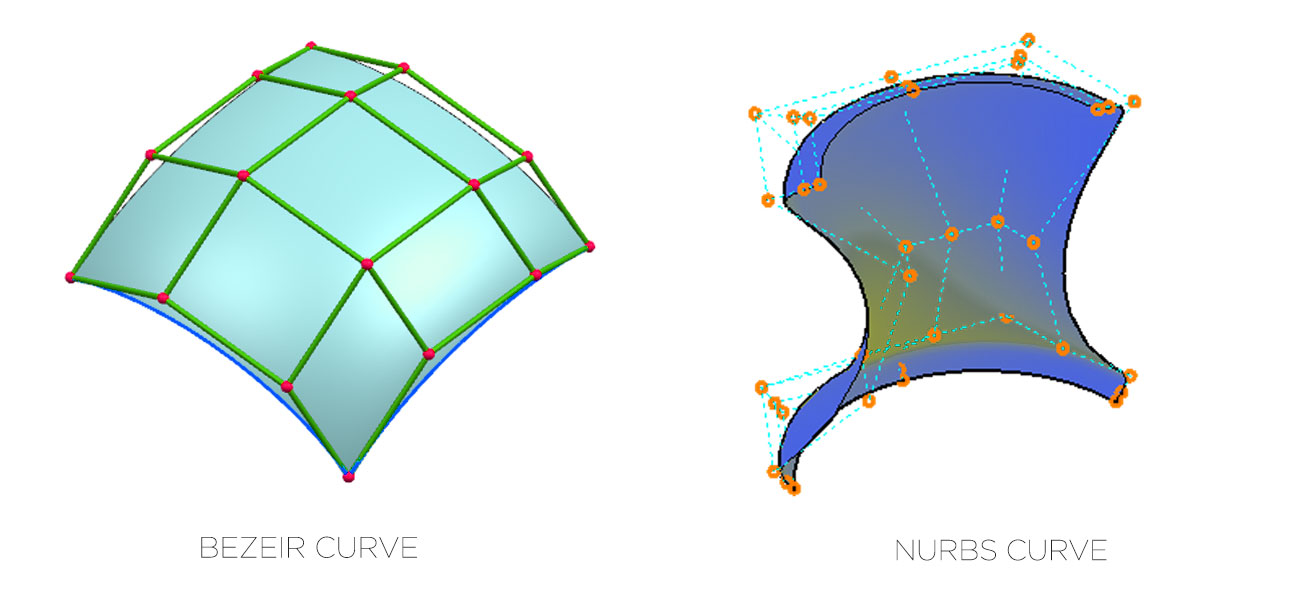
NURBS曲线是一种参数曲线，它结合了贝塞尔曲线（Bezier）和B样条曲线（B-spline）的优点。NURBS能够精确地表示规则和不规则的几何形状，这使得它成为了工业设计和计算机辅助设计（CAD）中的首选工具。NURBS曲线插值是指通过一系列控制点，生成一条平滑的曲线，该曲线既经过所有的控制点，同时又满足某些额外的条件。

## 1.2 NURBS曲线的特点

NURBS曲线的特点包括：

- **精确性**：NURBS曲线可以通过权值（weight）参数来控制其形状，使得曲线可以精确地表示复杂的几何形状。
- **可调性**：通过调整控制点和权值，可以很容易地修改NURBS曲线的形状。
- **通用性**：NURBS可以表示线性、圆弧、椭圆弧等多种形状，并且可以表达非封闭和封闭曲线以及曲面。

在下一章节中，我们将深入分析NURBS曲线插值的数学原理，为理解其高级应用奠定坚实的理论基础。

# 2. NURBS曲线插值理论分析

## 2.1 NURBS曲线插值的数学基础

### 2.1.1 参数化曲线与NURBS表示

参数化曲线是通过参数`t`来定义点`P(t)`在空间中的位置，从而描述一条平滑的曲线。NURBS（Non-Uniform Rational B-Splines）是一种在计算机图形学中广泛使用的参数化曲线表示方法。它结合了贝塞尔曲线和B样条曲线的优点，并加入了有理分量，使其能够精确地表示自由曲线和曲面，无论是在简单的几何形状还是在复杂的工业设计中。

NURBS曲线的一般形式可以表示为：
\[ C(t) = \frac{\sum_{i=0}^{n} N_{i,p}(t) w_i d_i}{\sum_{i=0}^{n} N_{i,p}(t) w_i} \]
其中，\(N_{i,p}(t)\)是p次B样条基函数，\(w_i\)是控制点的权重，\(d_i\)是控制点坐标。

### 2.1.2 插值与逼近的区别及原理

插值是指通过一组给定的点来构造一条曲线，这些点必须全部位于曲线上。而逼近则是指找到一条曲线，使其与给定点的距离在某种意义下最小化，但并不要求曲线通过这些点。

在NURBS曲线插值中，我们关心的是确保曲线通过一组特定的控制点。这种情况下，我们通常采用插值而不是逼近，因为NURBS曲线的控制点直接决定了曲线的形状。通过合理设置控制点的权重和位置，我们可以获得所需精确度的插值曲线。

## 2.2 NURBS曲线插值的算法探究

### 2.2.1 插值问题的数学模型构建

构建NURBS曲线的数学模型首先需要确定控制点和权重，然后选择合适的节点向量。节点向量是定义在参数空间中的有序数列，它决定了B样条基函数的形状和分布，从而影响曲线的局部变化。

构建模型的数学表达式通常涉及计算每个基函数`N_{i,p}(t)`在特定参数`t`下的值，并将其与相应的控制点加权求和。为了确保曲线通过特定的插值点，需要精心设计控制点和基函数。

### 2.2.2 插值算法的类型与选择

NURBS曲线插值算法的类型取决于给定插值点的数量和分布。常见的算法包括de Boor算法和Cox-de Boor递推公式，这些都是用来高效计算B样条曲线上的点。

选择合适的算法需要考虑以下几个因素：
- 插值点的数量
- 要求的精确度
- 计算效率

例如，对于线性插值，可以选择最简单的线性插值算法。如果曲线较为复杂，可能需要采用高阶插值算法。在软件实现中，可以通过比较不同算法在实际应用中的表现，根据具体需求选择最优算法。

## 2.3 NURBS曲线插值的性能考量

### 2.3.1 算法效率与复杂度分析

在NURBS曲线插值算法的设计中，算法效率是一个重要的考量指标。效率高的算法可以在较短的时间内处理大量的插值点，构建出平滑的曲线，这对于实时系统或者大规模数据处理尤为重要。

算法的时间复杂度和空间复杂度是评估算法效率的主要指标。时间复杂度涉及计算操作的数量，而空间复杂度涉及算法运行所需的存储空间。理想情况下，我们追求低时间复杂度和低空间复杂度的算法。

例如，递归算法虽然代码简洁，但可能会导致较高的时间复杂度。迭代算法通常有更低的复杂度，但可能需要更多的编程技巧来实现。

### 2.3.2 精度控制与误差分析

NURBS曲线插值的精度控制与误差分析是一个复杂的主题。在实际应用中，我们通常需要在计算效率和插值精度之间做出权衡。一般来说，增加控制点的数量和提高曲线的阶数可以提高插值的精度，但也会增加计算量和复杂度。

误差分析不仅涉及到算法内部的数值误差，还可能受到输入数据的不确定性和外部因素的影响。分析误差时，需要考虑以下几个方面：
- 数据的采样精度
- 计算过程中舍入误差的累积
- 控制点设置的合理性

通过软件测试和实验结果，我们可以对算法的精度进行评估，以确保其满足设计要求。在开发过程中，使用高精度的数据类型和合理的误差控制策略是提高NURBS曲线插值精度的关键。

## 2.4 NURBS曲线插值的应用场景

NURBS曲线插值除了在计算机图形学领域的应用外，还广泛应用于工程和科学计算。下面是一些典型的应用场景：

### 2.4.1 工程设计与制造

在工程设计和制造领域，精确的曲线和曲面表示是至关重要的。NURBS曲线插值允许工程师通过少量的控制点精确地定义复杂的形状，这些形状可以通过计算机数控（CNC）机床精确加工。从汽车到飞机的制造，NURBS技术的应用能够显著提高设计和制造的精度和效率。

### 2.4.2 科学可视化

在科学可视化中，NURBS曲线插值技术被用于三维数据的插值和渲染，以生成准确和美观的图表和动画。例如，在天气预测、流体动力学模拟以及地理信息系统中，NURBS曲线插值提供了强大的工具来展示和分析复杂的数据模式。

### 2.4.3 医学图像处理

医学图像处理领域同样利用NURBS技术进行图像插值和重建，从而在X光、MRI或CT扫描中获得更平滑和清晰的图像。这可以帮助医生更精确地诊断和治疗疾病。例如，通过插值算法可以重建出完整的三维模型，从而实现对器官或组织的详细分析。

### 2.4.4 游戏与影视动画

在游戏和影视动画制作中，NURBS技术用于创建和控制角色和场景中的平滑曲线和曲面。其灵活性允许动画师以更自然的方式设计复杂的动画路径，提高作品的质量和视觉吸引力。NURBS曲线插值技术在动画制作中扮演着关键角色，特别是在需要精确路径控制的情况下，如面部动画和物理模拟动画。

### 2.4.5 航空航天设计

在航空航天设计中，精确的曲线和曲面表示对于飞机、卫星等设计至关重要。NURBS曲线插值技术允许设计师创建复杂几何形状，并且精确控制这些形状。这不仅涉及到外观的设计，还包括了性能优化和重量分析等方面。通过NURBS曲线插值，设计师可以创建出既美观又高效的航空器和航天器。

### 2.4.6 产品设计与建模

产品设计与建模是NURBS曲线插值技术的另一个重要应用领域。从家具设计到复杂的机械设备，NURBS曲线插值技术为设计师提供了强大的工具来创建精确的模型和草图。这不仅可以加快设计过程，还可以提高设计的质量和创新性。例如，使用NURBS曲线插值技术，设计师可以轻松地修改和优化产品的形状，以达到最佳的功能和外观效果。

# 3. NURBS曲线插值的软件集成实践

## 3.1 集成前的准备工作

### 3.1.1 环境搭建与配置

在进行NURBS曲线插值的软件集成之前，环境搭建与配置是首要步骤。不同的开发环境和工具链可能会影响到代码的运行效率和可维护性。对于NURBS曲线插值来说，典型的软件集成环境需要包括但不限于以下组件：

- **开发工具**: 选择合适的IDE，如Visual Studio、Qt Creator等，以支持C++、Python或其他开发语言的编程和调试。
- **图形库**: 根据需要集成的平台，选择OpenGL、DirectX、Vulkan等图形库，以支持NURBS曲线的实时渲染和交互。
- **数学计算库**: 为了便于进行数值计算，比如矩阵操作、数值积分等，可集成如Eigen、Armadillo等数学计算库。
- **第三方工具**: 使用如Git进行版本控制，CMake或Meson等构建系统进行项目构建等。

在搭建开发环境时，需要确保所有依赖都得到满足，并进行适当的配置，例如设置环境变量，安装必要的SDK等。

### 3.1.2 集成前的代码审查和框架搭建

在进行集成之前，对现有代码进行审查是确保软件质量的关键。代码审查过程需要关注以下几个方面：

- **代码风格一致性**: 确保团队的代码风格保持一致，以便于代码的阅读和维护。
- **逻辑清晰性**: 代码逻辑需要清晰，易于理解。任何复杂的算法部分应当有详细的注释。
- **接口定义**: 明确定义各个模块之间的接口，确保它们之间的交互不会引起错误或不一致。

接下来是框架的搭建。框架的构建是一个精心设计的过程，需要考虑到将来可能的扩展性和可维护性。在构建NURBS曲线插值的框架时，重点应放在以下几个方面：

- **模块化设计**: 将NURBS曲线插值功能划分成多个模块，如数据结构模块、算法实现模块、用户界面模块等，每个模块有明确的职责。
- **抽象与封装**: 合理地抽象共通功能并进行封装，以减少代码冗余和提高代码复用性。
- **依赖管理**: 明确模块间的依赖关系，采用依赖注入等设计模式减少耦合度。

框架搭建是软件集成成功的关键。一个合理的框架可以确保后续集成工作的顺利进行。

## 3.2 NURBS曲线插值功能的代码实现

### 3.2.1 编写NURBS插值核心算法

NURBS曲线插值的核心算法是根据控制点、权重和节点向量来计算曲线上的点。以下是使用C++和Eigen库实现NURBS曲线插值核心算法的代码示例：

#include <Eigen/Dense>
#include <vector>

// 计算贝塞尔曲线上的点
Eigen::Vector3d CalculateBezierPoint(const std::vector<Eigen::Vector3d>& points, double t) {
    // ... 贝塞尔曲线计算逻辑 ...
}

// NURBS曲线插值核心算法
Eigen::Vector3d CalculateNURBSPoint(const std::vector<Eigen::Vector3d>& controlPoints,
                                    const std::vector<double>& weights,
                                    const std::vector<double>& knots,
                                    int degree, double t) {
    // 确保输入参数正确
    // ... 输入参数校验逻辑 ...

    // 构造贝塞尔曲线上的点
    Eigen::Vector3d pointOnCurve = CalculateBezierPoint(controlPoints, t);

    // ... 应用NURBS的权重和节点向量计算逻辑 ...

    return pointOnCurve;
}

int main() {
    // 示例控制点、权重和节点向量
    std::vector<Eigen::Vector3d> controlPoints = {/* 控制点数据 */};
    std::vector<do