SPWM在电力电子中的应用揭秘:案例分析与工具实践
发布时间: 2024-12-15 21:00:37 阅读量: 6 订阅数: 6 


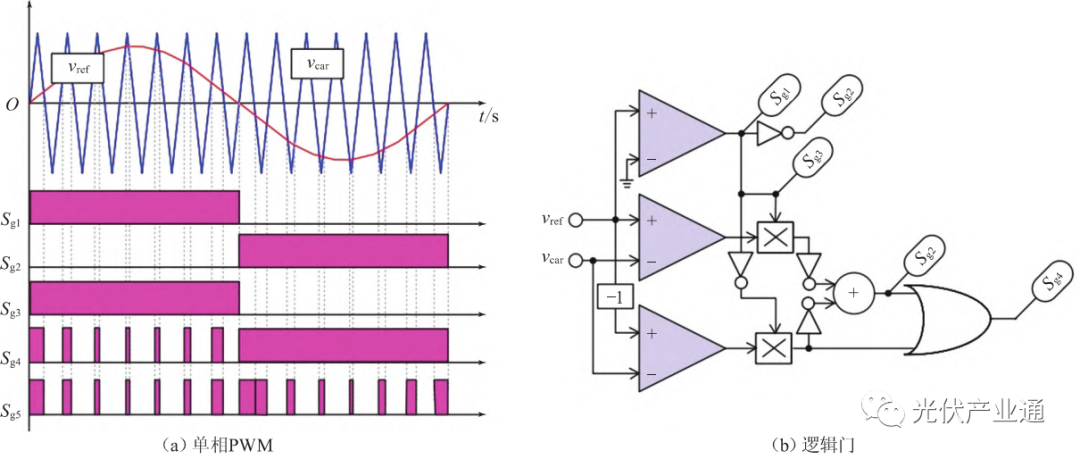
电力电子技术仿真-三相SPWM逆变电路的Simulink仿真
参考资源链接:[spwm_calc_v1.3.2 SPWM生成工具使用指南:简化初学者入门](https://wenku.csdn.net/doc/6401acfecce7214c316ede5f?spm=1055.2635.3001.10343)
# 1. SPWM在电力电子中的原理概述
## 1.1 SPWM技术简介
**SPWM(Sinusoidal Pulse Width Modulation)**是一种电力电子领域广泛应用的脉冲宽度调制技术。其核心思想是通过调整脉冲宽度,使输出信号的基波幅值和频率与输入的正弦波信号相匹配,而高次谐波含量则尽量减小。SPWM技术因具有减少输出谐波、改善波形质量的优点,在电机驱动、逆变器、变频器等电力转换系统中发挥着重要的作用。
## 1.2 SPWM的工作原理
SPWM的工作原理基于调制波与载波之间的一种比较。正弦波作为调制波,三角波作为载波,通过比较两者的瞬时值,产生宽度不同的脉冲序列。在调制过程中,当调制波的值高于载波时,脉冲输出高电平;反之,则输出低电平。这样的脉冲序列经过滤波器处理后,可以得到近似于正弦波的电压波形。
## 1.3 SPWM的优势
SPWM技术的一个显著优势是它能够有效地控制功率器件的开关,从而改善电力系统的动态响应和静态性能。它通过精细地控制脉冲的宽度和顺序,实现对电能质量的精确控制。此外,SPWM技术在能量转换效率和系统稳定性方面也有着突出的表现,因此在现代电力电子系统中占据着不可替代的地位。
通过以上内容,我们初步了解了SPWM技术的基本概念和它在电力电子中的重要性。接下来我们将深入探讨SPWM的理论基础与数学模型,以及它在实际应用中的表现与优化策略。
# 2. SPWM理论基础与数学模型
## 2.1 SPWM的基本原理
### 2.1.1 载波调制与SPWM生成
当谈论到脉宽调制(Pulse Width Modulation, PWM)时,通常会提及一系列的调制技术,其中正弦脉宽调制(Sinusoidal Pulse Width Modulation, SPWM)是电力电子领域中的一项关键技术,尤其在交流(AC)到直流(DC)的转换中扮演着重要的角色。SPWM的生成方法之一是通过载波调制技术,这种技术通过与一个正弦波信号相比较来调制一个高频载波信号,生成期望的SPWM波形。
在载波调制中,高频三角波载波信号与低频的正弦波参考信号进行比较。当正弦波信号的幅值高于三角波信号的幅值时,输出为高电平;反之则为低电平。通过这种方式,输出信号的脉宽与正弦波的瞬时值成正比,因此输出的SPWM信号在时域上模拟了正弦波的波形。
以一个简单的例子说明如何使用载波调制生成SPWM信号:
```python
import numpy as np
import matplotlib.pyplot as plt
# 设定参数
Amplitude = 1.0 # 正弦波的幅值
Frequency = 50.0 # 正弦波的频率 (Hz)
CarrierFreq = 1000.0 # 载波频率 (Hz)
SamplingFreq = 10000. # 采样频率 (Hz)
# 生成时间轴
t = np.arange(0, 0.01, 1/SamplingFreq)
# 生成正弦波信号与三角波载波信号
sine_wave = Amplitude * np.sin(2 * np.pi * Frequency * t)
carrier_wave = np.zeros(t.shape)
for i in range(len(t)-1):
if t[i] < t[i+1]:
carrier_wave[i] = (Amplitude*CarrierFreq) * ((2*(t[i] % (1.0/(CarrierFreq)))/((1.0/(CarrierFreq)))) - 1)
else:
carrier_wave[i] = carrier_wave[i-1]
# 进行比较生成SPWM信号
spwm_signal = np.where(sine_wave > carrier_wave, 1, 0)
# 绘制信号波形图
plt.figure(figsize=(10, 6))
plt.plot(t, sine_wave, label='Sine Wave')
plt.plot(t, carrier_wave, label='Carrier Wave')
plt.step(t, spwm_signal, where='post', label='SPWM Signal')
plt.title('SPWM Generation with Carrier Modulation')
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')
plt.legend()
plt.grid(True)
plt.show()
```
这段代码首先生成了一个正弦波和三角波信号,然后通过比较它们的值生成SPWM信号。通过Python的matplotlib库来可视化这三个信号。图中可以看到SPWM信号在时间上较好地模拟了正弦波的波形,但同时保留了高频载波的开关特性。
### 2.1.2 SPWM的基本参数和特性
SPWM波的生成依赖于几个关键参数:载波频率、调制深度以及输出频率。载波频率决定了开关器件的开关频率,对滤波器设计有着直接的影响。调制深度影响输出波形的幅值,进而影响输出功率和效率。输出频率则是由正弦波信号的频率决定,直接关联到最终应用中的电气特性,如电机速度。
SPWM信号的主要特性包括它能够有效地传输功率,同时减少输出波形中的低频谐波。这使得SPWM广泛应用于逆变器、变频器和电机驱动中。此外,SPWM技术还具备如下特性:
- 高频开关特性允许使用更小的滤波器元件。
- 能够适应各种负载条件,并保持较好的动态响应。
- 在交流电机控制中可以提供更好的转矩控制和效率。
理解这些基本参数和特性对于SPWM的正确应用和优化至关重要,尤其是在设计电力电子设备时。为了更深入理解SPWM的工作原理,接下来我们将探讨SPWM的数学描述。
## 2.2 SPWM的数学表达
### 2.2.1 正弦波与三角波的数学描述
在数学上,正弦波可以表达为:
\[ s(t) = A \sin(2\pi f t + \phi) \]
其中,\( A \) 是幅度,\( f \) 是频率,\( \phi \) 是相位角,\( t \) 是时间。三角波通常用锯齿波函数来描述:
\[ c(t) = A_c \left(2 \left\{\frac{f_c t}{T} - \left\lfloor\frac{f_c t}{T}\right\rfloor\right\} - 1\right) \]
这里,\( A_c \) 是三角波的幅值,\( f_c \) 是三角波频率,\( T \) 是三角波周期,而 \(\left\lfloor \cdot \right\rfloor\) 表示取下整函数。
在SPWM中,载波(三角
0
0






