【Java枚举与Kotlin密封类】：语言特性与场景对比分析

# 1. Java枚举与Kotlin密封类的基本概念

## 1.1 Java枚举的定义

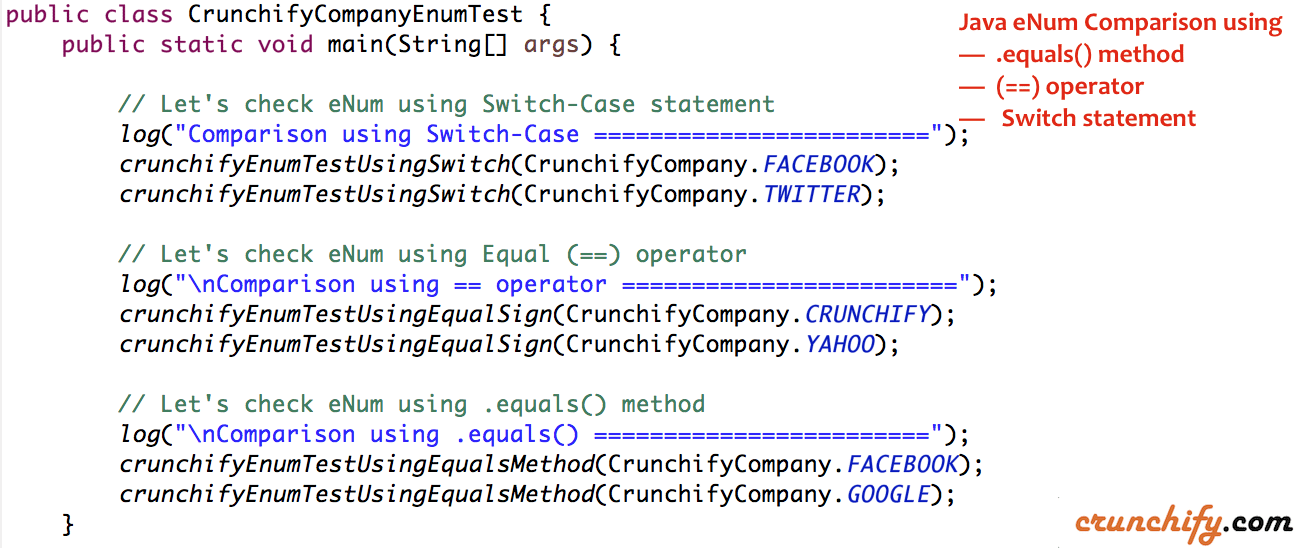
Java枚举是一种特殊的类，用来表示固定的常量集。它是`java.lang.Enum`类的子类。Java枚举提供了一种类型安全的方式来处理固定数量的常量，常用于替代传统的整型常量和字符串常量。

## 1.2 Kotlin密封类的定义

Kotlin密封类是一种限制类继承的类，用来表达受限的类层次结构。密封类不能被扩展，除了声明它们的文件中的类之外，其他类不能继承密封类。这使得在处理特定情况和使用模式匹配时能够更加安全和方便。

## 1.3 Java枚举与Kotlin密封类的共同点

虽然Java枚举与Kotlin密封类在形式和语言特性上有所不同，但它们在目的上是相似的。它们都用于定义一组受限的实例，并且能够提供类型安全的机制。在实际应用中，这两种语言特性都广泛用于表示一组状态或者有限的选择集，提升代码的可读性和可维护性。

# 2. Java枚举的内部实现与用法

## 2.1 Java枚举的定义和属性
### 2.1.1 枚举的基本语法
在Java中，枚举（enum）是一种特殊的数据类型，用于表示一组固定的常量。枚举类型是通过关键字`enum`来定义的，它的声明位置和类一样，在任何可以声明类的地方都可以声明枚举类型。每个枚举类型都隐式地继承自`java.lang.Enum`类。下面是一个简单的枚举示例：

public enum Day {
    // 枚举值
    MONDAY, TUESDAY, WEDNESDAY, THURSDAY, FRIDAY, SATURDAY, SUNDAY;
}

在这个例子中，`Day`是一个枚举类型，它包含七个枚举值，每个值都是`Day`类型的一个实例。在Java中，枚举常量默认都是`public static final`的，且在类加载的时候会被初始化。

### 2.1.2 枚举的构造函数和字段
与普通类一样，枚举类型也可以有自己的构造函数、字段和方法。构造函数在枚举类型中是私有的，这意味着它们不能从类的外部访问。在枚举中声明字段和方法，可以为每个枚举实例提供特定的值和行为。

public enum Day {
    MONDAY("星期一"),
    TUESDAY("星期二"),
    WEDNESDAY("星期三"),
    // 其他枚举值...
    ;

    private final String chineseName;

    // 私有构造函数
    private Day(String chineseName) {
        this.chineseName = chineseName;
    }

    public String getChineseName() {
        return chineseName;
    }
}

在这个例子中，枚举`Day`有一个私有的构造函数，它接受一个`String`参数。每个枚举实例都有一个对应的中文名称，这个名称被存储在`chineseName`字段中。`getChineseName`方法用于获取这个字段的值。

## 2.2 Java枚举的方法和行为
### 2.2.1 枚举的方法定义
枚举类型中可以定义方法，这些方法可以应用于枚举中的每个实例。除了构造函数外，还可以定义实例方法、静态方法甚至是抽象方法。抽象方法必须在每个枚举实例中被具体实现。

public enum Operation {
    PLUS {
        @Override
        public double apply(double x, double y) {
            return x + y;
        }
    },
    MINUS {
        @Override
        public double apply(double x, double y) {
            return x - y;
        }
    },
    // 其他操作...
    ;

    public abstract double apply(double x, double y);
}

在这个例子中，`Operation`枚举定义了一个抽象方法`apply`，每个枚举实例都必须提供`apply`方法的具体实现。这个方法定义了对应于每个操作的数学运算。

### 2.2.2 枚举与接口的实现
枚举可以实现接口，这是枚举提供额外行为的一种方式。通过实现接口，枚举可以被用于多种上下文中，例如作为策略模式的一部分。

public interface Operation {
    double apply(double x, double y);
}

public enum OperationEnum implements Operation {
    PLUS('+') {
        @Override
        public double apply(double x, double y) {
            return x + y;
        }
    },
    MINUS('-') {
        @Override
        public double apply(double x, double y) {
            return x - y;
        }
    },
    // 其他操作...
    ;

    private final char symbol;

    OperationEnum(char symbol) {
        this.symbol = symbol;
    }

    @Override
    public String toString() {
        return String.valueOf(symbol);
    }
}

在这个例子中，`OperationEnum`枚举实现了`Operation`接口，每个枚举值都关联了一个字符表示的操作符，例如`'+'`或`'-'`。`toString`方法被重写以返回操作符字符，这可以用于显示或序列化枚举值。

## 2.3 Java枚举的应用场景
### 2.3.1 枚举在状态管理中的应用
在状态管理中，枚举可以用来表示固定数量的状态。它们是处理状态转换的完美选择，因为枚举的实例是预定义且不可变的。

public enum TransactionStatus {
    PENDING, APPROVED, DECLINED, REFUNDED;
}

在这个场景中，`TransactionStatus`枚举可以用来跟踪交易的状态。由于枚举的类型安全，编译器可以在编译时就捕获到无效状态的错误，从而避免了运行时的错误。

### 2.3.2 枚举在模式匹配中的应用
Java 17引入了模式匹配的特性，这是Java语言对枚举类型支持的扩展。模式匹配可以用来简化条件逻辑，特别是在处理枚举类型时。

public enum Operation {
    PLUS, MINUS, MULTIPLY, D