计算机图形学秘籍：坐标变换优化策略大公开


参考资源链接：[原理详解_三点解算两个坐标系之间的旋转矩阵和平移向量](https://wenku.csdn.net/doc/6412b723be7fbd1778d49388?spm=1055.2635.3001.10343)
# 1. 计算机图形学中的坐标变换概述

计算机图形学是计算机科学的一个分支，专注于数字视觉信息的创建、处理、存储和显示。在这一领域中，坐标变换起着至关重要的作用，因为它允许图形和动画系统正确地模拟物体在虚拟空间中的移动和旋转。

## 1.1 坐标变换的重要性

坐标变换是从一个坐标系到另一个坐标系的转换过程。在计算机图形学中，它被广泛应用于3D建模、动画制作、视图转换以及渲染等场景。正确地进行坐标变换，能够保证场景中的对象以正确的方式渲染在屏幕上，包括它们的大小、位置和方向。

## 1.2 坐标变换的类型

在图形学中，最常见的坐标变换类型包括：

- 平移（Translation）：沿指定方向移动物体一定距离。
- 缩放（Scaling）：改变物体的大小。
- 旋转（Rotation）：围绕某个轴旋转物体。
- 变换组合（Transformation Composition）：将多个变换组合在一起应用。

每一种变换类型都对应着特定的数学公式和矩阵操作。理解这些基础变换对于深入学习图形学的坐标变换至关重要。

下面章节将详细介绍这些基础变换以及它们在图形学中的应用。

# 2. 基础坐标变换理论

## 2.1 线性代数在坐标变换中的应用

### 2.1.1 向量和矩阵的基础知识

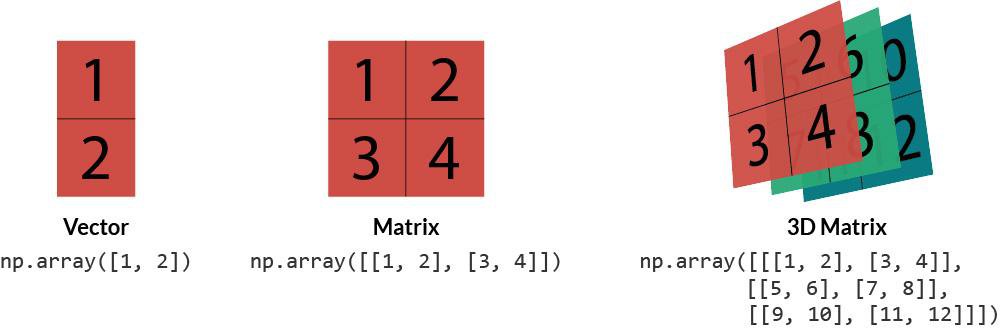
向量是坐标变换的基础，它可以看作是一个有序数列，表示为从原点到一个点的有向线段。在二维空间中，向量可以表示为 (x, y)，而在三维空间中表示为 (x, y, z)。矩阵则是线性代数中的一个核心概念，它是一种按照长方阵列排列的复数或实数集合。在坐标变换中，矩阵通常用来表示线性变换，如缩放、旋转和平移。

例如，一个二维向量可以被表示为一个 2x1 的矩阵（列向量），而变换矩阵则是一个 2x2 的矩阵：

v = |x|
    |y|

T = |a  b|
    |c  d|

在这个例子中，向量 v 可以通过矩阵 T 进行变换，变换后的向量 v' 是 T 和 v 的乘积。当讨论三维坐标变换时，向量和矩阵的维度将相应增加，例如，三维向量将表示为 3x1 的矩阵，而变换矩阵则变成 3x3。

### 2.1.2 矩阵乘法与坐标变换

矩阵乘法是实现坐标变换的关键操作。在进行矩阵乘法时，每个向量分量与矩阵的对应行相乘，并将结果求和，以此得到变换后的向量分量。例如，一个二维向量 v 经过变换矩阵 T 的操作可以表示为：

v' = T * v

具体运算过程如下：

| x' |   | a  b |   | x |
| y' | = | c  d | * | y |

在这个操作中，x' 和 y' 分别是变换后向量的新坐标。矩阵乘法是不可交换的，即 T * v 不等于 v * T。此外，注意矩阵乘法中行数必须与列数相匹配，即只有当 T 是 2x2 矩阵，v 是 2x1 列向量时，上述乘法才是合法的。

## 2.2 二维坐标变换的深入解析

### 2.2.1 平移、缩放、旋转和反射变换

坐标变换包括多种类型，每种变换在矩阵表示上都有其特定形式。

- **平移变换**不涉及矩阵乘法，而是通过向量加法实现。平移向量 (tx, ty) 可以通过在变换矩阵中引入额外的一列来实现：

Ta = | 1  0  tx |
     | 0  1  ty |
     | 0  0   1 |

- **缩放变换**通过缩放因子 sx 和 sy 对 x 和 y 分量进行缩放：

S = | sx  0   0 |
    | 0   sy  0 |
    | 0   0   1 |

- **旋转变换**，假设绕原点旋转角度 θ：

R(θ) = | cos(θ)  -sin(θ)  0 |
       | sin(θ)   cos(θ)  0 |
       |    0         0    1 |

- **反射变换**可以看作是一种特殊的变换，例如绕 x 轴的反射：

Rx = | 1   0   0 |
     | 0  -1   0 |
     | 0   0   1 |

### 2.2.2 变换的组合与逆变换

多个变换可以组合成一个单一的变换，这是因为矩阵乘法是可结合的。如果要将两个变换 T1 和 T2 依次应用到一个向量 v 上，可以计算这两个变换矩阵的乘积 T1*T2，并将结果应用到 v 上：

Tcombined = T1 * T2
v' = Tcombined * v

矩阵乘法的这种性质极大地简化了复杂的变换序列。

逆变换则用于撤销之前的变换操作，每种变换的逆变换都可以通过计算对应变换矩阵的逆矩阵得到。例如，旋转变换 R(θ) 的逆变换是 R(-θ)。

## 2.3 三维坐标变换的探索

### 2.3.1 三维空间中的线性变换

三维空间中的线性变换与二维类似，但是涉及到更多的维度和计算复杂性。三维变换矩阵是一个 4x4 的矩阵，它能够表示包括旋转变换在内的多种变换。三维向量则需要扩展为 4x1 的齐次坐标向量，即向量的最后一个分量为 1。在三维空间中，变换矩阵能够表示的变换类型更加丰富，包括但不限于三维空间的缩放、旋转、错切等。

### 2.3.2 视图变换和投影变换基础

视图变换用于将物体坐标系中的点转换到摄像机坐标系中，而投影变换则是为了将三维场景投影到二维屏幕平面上。这两种变换通常一起使用，视图变换可以通过一个4x4矩阵实现，而投影变换可以使用透视投影或正交投影矩阵。这些变换是三维图形渲染管线的关键部分，对于实现正确的视角和投影效果至关重要。

视图变换示例矩阵：

V = | 1   0   0  -tx |
    | 0   1   0  -ty |
    | 0   0   1  -tz |
    | 0   0   0   1  |

正交投影变换示例矩阵：

Ortho = | 2/n   0     0    0 |
        | 0     2/m   0    0 |
        | 0     0    -1/(f-n)  0 |
        | 0     0    0     n/(n-f) |

透视投影变换示例矩阵：

Perspective = | n   0     0    0 |
              | 0   n     0    0 |
              | 0   0   -(f+n)/(f-n)  -2fn/(f-n) |
              | 0   0    -1            0 |

以上就是对三维坐标变换基础的初步探索，这些变换的组合与实现构成了现代计算机图形学的核心。在后续章节中，我们将深入探讨如何优化这些变换的算法，以及它们在不同领域的实际应用。

# 3. 坐标变换算法优化实践

## 3.1 坐标变换算法的性能瓶颈
### 3.1.1 时间复杂度分析
在坐标变换算法中，时间复杂度是指完成算法所需的计算步骤数随输入数据规模增加而变化的趋势。对于变换矩阵与向量的乘法，假设变换矩阵为n×n大小，那么乘法操作的时间复杂度为O(n^2)。在一些高性能应用中，比如实时渲染或游戏引擎，这样的时间复杂度可能会成为性能瓶颈，尤其是在变换大量顶点时。

时间复杂度对性能的影响并非线性，与具体实现和硬件架构紧密相关。例如，现代GPU支持并行处理，可能会使得高时间复杂度的算法在实际应用中的性能表现优于理论上的预期。但即便如此，优化算法以降低时间复杂度仍然是提高性能的关键。

### 3.1.2 空间复杂度分析
空间复杂度是指算法在运行过程中临时占用存储空间的大小。在坐标变换中，空间复杂度主要与变换矩阵的存储有关。一个n×n的变换矩阵需要n^2个空间单位来存储。优化空间复杂度，可以减少内存的使用和提高缓存的效率。

在实践中，空间复杂度常常与时间复杂度进行权衡。例如，通过牺牲空间来换取计算速度的提升，比如使用空间局部性原理来提高缓存命中率。

## 3.2 实现高效坐标变换的策略
### 3.2.1 分块矩阵操作
分块矩阵操作是一种优化矩阵运算的策略，它通过将大矩阵划分成小块进行操作，从而利用现代CPU和GPU的多核优势，达到并行处理的目的。在一些算法中，分块矩阵操作可以显著提升性能。

例如，若要在三维空间中对一系列顶点进行变换，可以将顶点数据分组，并且并行计算每个分组的变换结果。每个分组的数据可以加载到GPU的不同线程中进行处理，这不仅减少了线程之间的等待，还提升了内存访问的效率。

### 3.2.2 GPU加速技术应用
利用GPU的并行处理能力，可以大幅提高坐标变换的速度。GPU是为图形渲染而设计的，能够同时处理大量的顶点和像素数据，这与坐标变换算法高度契合。

在优化坐标变换时，可以利用如OpenGL或DirectX中的顶点着色器或计算着色器来进行矩阵乘法。这些着色器在GPU上运行，可以同时处理成千上万的顶点，大大减少单个顶点变换所需的时间。

// 一个简单的OpenGL顶点着色器示例，用于顶点坐标变换
#version 330 core
layout (loca