【环境控制系统中的MATLAB控制算法应用】：探索智能与绿色科技的结合

# 1. 环境控制系统概述与需求分析

环境控制系统是现代智能建筑和工业自动化领域不可或缺的一部分。随着技术的发展，对于环境控制系统的要求也越来越高，不仅要确保环境的舒适性，还需考虑到节能减排与可持续发展的问题。本章首先从环境控制系统的基本概念入手，介绍其组成、作用以及在不同领域的应用情况。接着，本章深入分析了环境控制系统的核心需求，包括但不限于系统的稳定性、响应速度、精确度以及适应性。此外，还将探讨不同环境变量（如温度、湿度、光照等）对系统性能的影响，并对如何量化这些需求参数进行说明。

## 1.1 环境控制系统的组成与应用

环境控制系统通常由传感单元、控制单元、执行机构以及人机界面组成。传感单元负责收集环境数据；控制单元通过算法处理这些数据并作出决策；执行机构按照控制命令调节环境；人机界面则用于操作者与系统交互。应用层面，环境控制系统广泛应用于智能建筑、温室大棚、精密实验室、数据中心等领域，以确保环境的恒定性或根据特定需求进行调整。

## 1.2 系统需求分析的重要性

在环境控制系统的设计与实施过程中，需求分析是至关重要的一步。它涉及到系统性能的预期目标、功能的必要性、操作的便捷性以及成本的控制等方面。需求分析可以确保所设计的系统能够在预算内满足用户的需求，并能在实际操作中实现预期的效果。为此，需要采用系统化的方法，例如，KANO模型和QFD（质量功能展开）工具来帮助我们进行深入的需求挖掘和分析，以制定出最适合用户需求的环境控制方案。

通过对环境控制系统进行充分的概述与需求分析，可以为后续章节中更详细的系统建模、算法设计以及仿真验证工作打下坚实的基础。

# 2. MATLAB基础与控制算法理论

## 2.1 MATLAB软件介绍及其在控制领域的应用

### 2.1.1 MATLAB的特点与工具箱概述

MATLAB（Matrix Laboratory的缩写）是一种高性能的数值计算环境和第四代编程语言。它由MathWorks公司开发，并广泛应用于工程计算、数据分析、算法开发以及仿真等领域。MATLAB的核心是矩阵运算，它可以方便地处理向量和矩阵的运算，简化了科学计算的复杂性。

MATLAB的主要特点包括：

- **强大的数学运算能力**：它能够执行基本的矩阵运算、线性代数、统计学和数值分析等。
- **丰富的工具箱（Toolbox）**：这些预编程的函数集合提供了特定领域的高级功能，如图像处理、信号处理、控制系统等。
- **直观的集成开发环境（IDE）**：提供代码编辑器、命令窗口和图形用户界面，便于用户进行代码编写和调试。
- **高质量的图形和可视化功能**：可以创建2D和3D图表，用于数据可视化和结果展示。
- **与其他编程语言的接口**：支持与C/C++、Java、.NET等语言的接口，方便与其他应用程序集成。

MATLAB在控制领域中的应用主要依托于其控制工具箱，该工具箱为控制系统的建模、分析和设计提供了一系列强大的函数。例如，控制系统工具箱提供了函数用于创建传递函数、状态空间模型、绘制根轨迹、伯德图等，极大地促进了控制算法的研究与开发。

### 2.1.2 MATLAB在环境控制中的作用

在环境控制领域，MATLAB可应用于系统建模、算法开发、性能分析以及控制系统的仿真与优化。环境控制系统涉及到温湿度控制、光照强度调节、空气质量监测等多个方面，这些系统的设计需要精确的数学模型和高效的算法。

MATLAB在环境控制中的作用具体体现在：

- **系统建模**：通过使用MATLAB可以构建环境控制系统的数学模型，如使用传递函数或状态空间模型来表示物理过程。
- **算法开发与测试**：MATLAB控制工具箱提供的算法，如PID控制器、状态观测器等，可以在此基础上进行开发和测试。
- **性能评估**：通过仿真工具箱进行模拟测试，评估控制系统的稳定性、准确性和鲁棒性。
- **优化设计**：利用MATLAB的优化工具箱，可以对控制参数进行优化，以达到预期的控制性能。

MATLAB在环境控制系统中的应用，不仅限于理论研究，还涉及到实际项目的开发。在实际应用中，MATLAB可以辅助工程师快速地进行系统设计，验证控制策略的有效性，缩短产品从设计到市场的时间。

## 2.2 控制算法理论基础

### 2.2.1 系统建模与控制理论概述

在控制理论中，对系统进行建模是进行分析和控制设计的基础。系统建模是指利用数学语言描述系统的行为，构建数学模型以便分析和控制。数学模型可以是线性的也可以是非线性的，最常见的线性模型包括传递函数和状态空间模型。

**传递函数模型**通常用于描述系统的输入输出关系，表示为输出变量与输入变量的比值。传递函数是拉普拉斯变换后的结果，用以简化控制系统的分析和设计。传递函数可以用于分析系统的稳定性、稳态性能和瞬态响应等。

**状态空间模型**则从系统的内部状态入手，描述系统状态随时间变化的动态行为。状态空间模型由一组一阶微分方程组成，包含系统的状态变量、输入和输出。状态空间模型更适合于复杂系统的分析与综合，特别是对于多变量和非线性系统。

控制理论的核心是设计一个控制器，使得系统在受到干扰或参数变化时，仍能保持期望的性能。经典控制理论中，PID（比例-积分-微分）控制器是最常见的控制算法。PID控制器通过调整比例（P）、积分（I）和微分（D）三个参数来实现对系统输出的精确控制。

### 2.2.2 PID控制算法的原理与应用

PID控制算法的原理基于对误差信号的三个分量进行处理：

- **比例（P）**：对当前误差进行放大，产生一个与误差大小成比例的控制量。
- **积分（I）**：对误差进行时间积分，消除稳态误差，提高系统的长期精确度。
- **微分（D）**：对误差变化率进行预测，实现超前控制，减小系统的振荡。

在MATLAB中，可以通过控制工具箱快速实现PID控制器的设计和仿真。以下是一个简单的示例代码块，展示如何在MATLAB中创建一个PID控制器并应用于一个传递函数模型：

% 假设有一个传递函数模型
G = tf(1, [1 10 20]);

% 设计一个PID控制器
Kp = 25; Ki = 30; Kd = 5; % 这些值通常需要根据实际系统进行调整
C = pid(Kp, Ki, Kd);

% 闭环系统的传递函数
T = feedback(C*G, 1);

% 进行仿真测试
step(T);
grid on;

% 代码后附加解释说明参数如何影响系统行为

每个参数的选择都会对系统性能产生影响。通常，比例增益Kp负责改善系统的响应速度，积分增益Ki有助于消除稳态误差，微分增益Kd则可以减少系统的超调和振荡。

## 2.3 算法性能分析与设计指标

### 2.3.1 稳定性、准确性和鲁棒性分析

在控制系统设计中，稳定性、准确性和鲁棒性是衡量系统性能的三个关键指标。

- **稳定性**：系统在受到扰动后能够返回到平衡状态的能力。在控制理论中，有多种分析稳定性的方法，如劳斯稳定性判据、奈奎斯特图和根轨迹分析等。
- **准确性**：系统输出能够达到期望参考输入的能力。准确性的高低通常由系统的稳态误差来衡量，对于一个理想的系统，稳态误差应该尽可能的小。
- **鲁棒性**：系统对于参数变化和外部干扰的不敏感性。鲁棒控制系统能够在一定的参数变化范围内保持性能不下降。

### 2.3.2 控制算法性能指标的确定

确定控制算法性能指标是控制系统设计的一个重要环节。这些指标包括：

- **超调量**：系统输出超过期望值的最大量，通常用百分比表示。
- **上升时间**：系统输出达到稳态值的90%所需的时间。
- **稳态误差**：系统在稳态时，输出与期望输入之间的偏差。
- **调整时间**：系统输出达到并保持在期望误差带内所需的时间。

在MATLAB中，可以使用控制系统工具箱中的函数来分析系统的性能指标。例如，使用`step`函数可以得到系统的阶跃响应，从而分析超调量和上升时间。使用`margin`函数可以分析系统的增益裕度和相位裕度，从而判断系统的稳定性。

以下是一个使用MATLAB评估控制系统性能的示例：

% 假设有一个传递函数模型
G = tf(1, [1 10 20]);

% 设计一个PID控制器
C = pid(25, 30, 5);

% 闭环系统的传递函数
T = feedback(C*G, 1);

% 分析系统的阶跃响应
figure;
step(T);
grid on;

% 计算并显示性能指标
[~,~,~,overshoot,settlingTime] = stepinfo(T);

% 显示性能指标
fprintf('超调量: %.2f%%\n', overshoot);
fprintf('调整时间: %.2f秒\n', settlingTime);

通过对性能指标的分析，可以调整PID参数以达到更优的控制效果。这个过程可能需要反复迭代，直到满足设计要求为止。MATLAB为这一过程提供了强大的工具和直观的分析，极大地简化了控制算法的性能评估和参数调整。

### 2.3.3 设计实例与性能优化

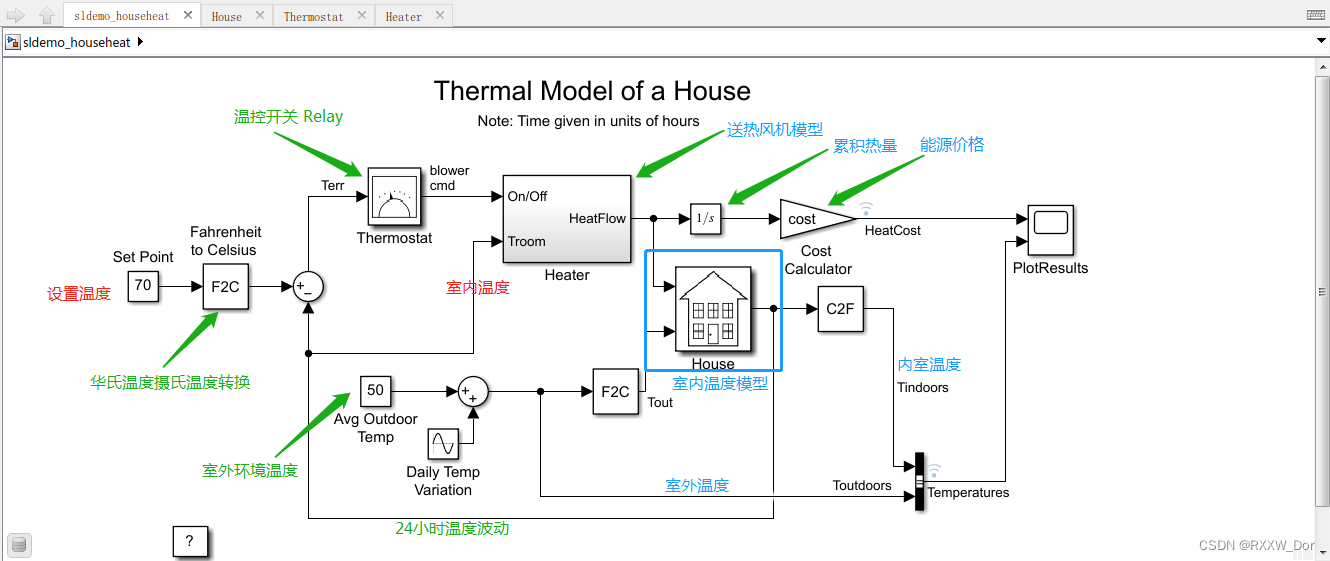
控制算法的设计与优化通常涉及到一系列迭代的步骤，需要对控制系统的性能进行评估和参数调整。以下是设计一个温度控制系统的过程实例。

首先，我们需要建立温度控制系统的数学模型。假设我们有一个电加热元件，其温度受加热功率控制。我们可以将温度变化视为一阶系统，并创建一个传递函数模型来描述这个系统：

% 创建一个电加热元件的传递函数模型
K = 1; % 温度增益
tau = 100; % 时间常数，单位秒
G = tf(K, [tau 1]);

接下来，我们设计一个PID控制器，并使用PID Tuner工具来自动调整PID参数：

% 使用PID Tuner工具
pidTuner(G, 'pid');

在PID Tuner界面中，我们可以手动调整PID参数，并观察阶跃响应，以达到最佳性能。我们可以通过拖动比例、积分、微分滑块或者输入具体数值来进行调整。

调整完成后，我们可以将优化的PID参数应用到系统中：

% 获取PID Tuner优化后的参数
[Coptim, info] = pidTuner(G, 'pid');

然后，我们可以评估优化后的控制器性能：

% 分析系统的阶跃响应
figure;
step(Coptim*G);
grid on;

% 计算并显示性能指标
[~,~,~,overshoot,settlingTime] = step